Engage NY Eureka Math Geometry Module 4 Mid Module Assessment Answer Key
Eureka Math Geometry Module 4 Mid Module Assessment Task Answer Key
For problems that require rounding, round answers to the nearest hundredth, unless otherwise stated.
Question 1.
You are a member of your school’s robotics team and are in charge of programming a robot that will pick up Ping – Pong balls. The competition arena is a rectangle with length 90 feet and width 95 feet.
On graph paper, you sketch the arena as a rectangle on the coordinate plane with sides that are parallel to the coordinate axes and with the southwest corner of the arena set at the origin. Each unit width on the paper grid corresponds to 5 feet of length of the arena. You initially set the robot to move along a straight path at a constant speed. In the sketch, the robot’s position corresponds to the point (10, 30) in the coordinate plane at time t = 2 seconds and to the point (40, 75) at time t = 8 seconds.
a. Sketch the arena on the graph paper below, and write a system of inequalities that describes the region in the sketch.
Answer:
0 ≤ x ≤ 95
0 ≤ y ≤ 90
b. Show that at the start, that is, at time t = 0, the robot was located at a point on the west wall of the arena. How many feet from the southwest corner was it?
Answer:
(0, 15), 15 feet North Each second, the robot travels 5 feet right and 7.5 feet up. If at 2 seconds the robot is at (10, 30), then moving left 10 units and down 15 units brings it to (0, 15).
c. What is the speed of the robot? Round to the nearest whole number.
Answer:
9 ft/sec
d. Write down an equation for the line along which the robot moves.
Answer:
y = \(\frac{3}{2}\) x + 15
e. At some time the robot will hit a wall. Which wall will it hit? What are the coordinates of that point of impact?
Answer:
North (top) wall at (50, 90)
f. How far does the robot move between time t = 0 seconds and the time of this impact? What is the time for the impact? Round distance to the nearest hundredth and time to the nearest second.
Answer:
Distance of 90.14 feet at time 10 seconds
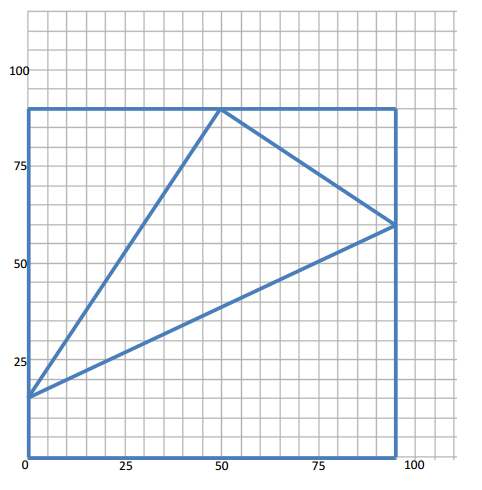
At the time of impact, you have the robot come to a gentle halt and then turn and head in a direction perpendicular to the wall. Just as the robot reaches the opposite wall, it gently halts, turns, and then returns to start. (We are assuming that the robot does not slow down when it hits a wall.) The robot thus completes a journey composed of three line segments forming a triangle within the arena. Sketch the path of the robot’s motion.
g. What are the coordinates where it hits the east wall?
Answer:
(95, 60)
h. What is the perimeter of that triangle? Round to the nearest hundredth.
Answer:
249.34 feet
i. What is the area of the triangle? Round to the nearest tenth.
Answer:
2437.5 square feet
j. If the count of Ping – Pong balls in the arena is large and the balls are spread more or less evenly across the whole arena, what approximate percentage of balls do you expect to lie within the triangle the robot traced? (Assume the robot encountered no balls along any legs of its motion.)
Answer:
28.51%
Question 2.
Consider the triangular region in the plane given by the triangle (1, 6), (6, – 1), and (1, – 4).
a. Sketch the region, and write a system of inequalities to describe the region bounded by the triangle.

Answer:
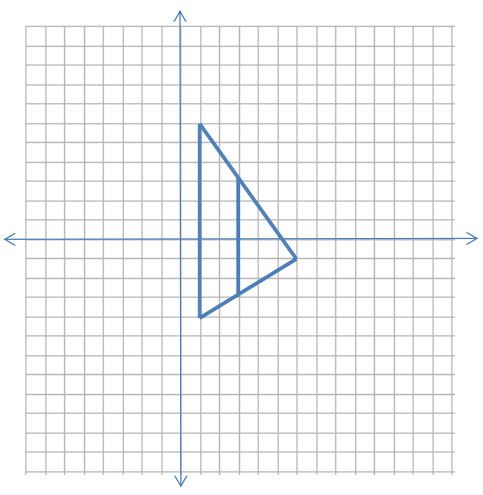
x ≥ 1
7x + 5y ≤ 37
3x – 5y ≤ 23
b. The vertical line x = 3 intersects this region. What are the coordinates of the two boundary points it intersects? What is the length of the vertical segment within the region between these two boundary points?
Answer:
(3, \(\frac{16}{5}\)), (3, –\(\frac{14}{5}\))
Length of segment is 6 units
c. The line x = 3 divides the region into a quadrilateral and a triangle. Find the perimeter of the quadrilateral and the area of the triangle.
Answer:
Perimeter of quadrilateral is 21.84 units.
Area of triangle is 9 square units.
Question 3.
Is triangle RST, where R(4, 4), S(5, 1), T( – 1, – 1), a right triangle? If so, which angle is the right angle? Justify your answer.
Answer:
The triangle is a right triangle. The slopes of the segments \(\overline{R S}\) and \(\overline{S T}\) (-3 and \(\frac{1}{3}\), respectively) are negative reciprocals, so \(\overline{R S}\) and \(\overline{S T}\) are perpendicular, making ∠S the right angle. The converse of the Pythagorean theorem is true because the sides lengths are \(\sqrt{10}\), \(\sqrt{40}\), and \(\sqrt{50}\).
Question 4.
Consider the points A( – 1, 3) and B(6, 2) in the coordinate plane. Let O(0, 0) be the origin.
a. Find the coordinates of a point, C, away from the origin on the line y = x that make triangle ABC a right triangle with a right angle at C.
Answer:
Since C is on the y = x line, the coordinate of the point can be C (x,x) or C (y,y) . Translate C to O :
A’ (-1 – x, 3 – x)
B’ (6 – x, 2 – x)
Then:
(-1 – x )(6 – x) + (3 – x )(2 – x)=0
-6 + x-6x + x2 + 6-3x-2x + x2 = 0
x2 – 5x = 0
x (x – 5)= 0
x = 0, 5
If x = 0, then the coordinate of C is (0,0) .
If x = 5, then the coordinate of C is (5, 5) . Since C was said to be away from the origin, the coordinate must be (5, 5) .
b. Find the coordinates of a point, D, on the line y = x that make triangle OBD a right triangle with right angle at B.
Answer:
Since D is on the y = x line, the coordinate of the point can be D(x, x) or D(y, y) . Translate B to O :
O’ (-6, -2)
D’ (x – 6, x – 2)
Then:
-6 (x – 2 ) ± [-2 (x – 2 )] = 0
-8x + 40 = 0
x = 5
If x = 5, then the coordinate of D is (5, 5) .
Question 5.
Consider the quadrilateral with vertices ( – 2, – 1), (2, 2), (5, – 2), and (1, – 5).
a. Show that the quadrilateral is a rectangle.
Answer:
Both pairs of opposite sides of the quadrilateral are parallel (slopes \(\frac{3}{4}\) and –\(\frac{4}{3}\)), and the slopes are negative reciprocals; so, the sides are perpendicular to each other, meaning all angles are right angles.
b. Is the quadrilateral a square? Explain.
Answer:
All sides have an equal length of 5 units. A rectangle with all sides of equal lengths is a square.
c. What is the area of the quadrilateral?
Answer:
The area is 25 square units.
d. What is the area of the region of the quadrilateral that lies to the right of the y – axis?
Answer:
The area is \(\frac{125}{6}\) square units.
e. What is the equation of the perpendicular bisector of the side of the quadrilateral that lies in the fourth quadrant?
Answer:
y = – \(\frac{4}{3}\) x + \(\frac{1}{2}\)
Question 6.
Using the general formula for perpendicularity of segments with one endpoint at the origin, determine if the segments from the given points to the origin are perpendicular.
a. (4, 10), (5, – 2)
Answer:
4 ∙ 5 + 10 ∙ (-2 ) = 0 ; the segments are perpendicular.
b. ( – 7, 0), (0, – 4)
Answer:
-7∙0 + 0∙(- 4 ) = 0 ; the segments are perpendicular.
c. Using the information from part (a), are the segments through the points ( – 3, – 2), (1, 8), and (2, – 4) perpendicular? Explain.
Answer:
The segments are perpendicular because they are a translation (right 3 units, up 2 units) of the segments in part (a) that are perpendicular.
Question 7.
Write the equation of the line that contains the point ( – 2, 7) and is
a. Parallel to x = 3.
Answer:
x = -2
b. Perpendicular to x = – 3.
Answer:
y = 7
c. Parallel to y = 6x – 13.
Answer:
y = 6x + 19
d. Perpendicular to y = 6x – 13.
Answer:
y = – \(\frac{1}{6}\) x + \(\frac{20}{3}\)
Question 8.
Line A contains points (p – 4, 2) and ( – 2, 9). Line B contains points (p, – 1) and ( – 1, 1).
a. Find the value of p if the lines are parallel.
Answer:
p = –\(\frac{11}{5}\)
b. Find the value(s) of p if the lines are perpendicular.
Answer:
p = 4 , p = -3