Engage NY Eureka Math Geometry Module 5 Lesson 19 Answer Key
Eureka Math Geometry Module 5 Lesson 19 Example Answer Key
Example 1.
Consider the circle with equation (x – 3)2 + (y – 5)2 = 20. Find the equations of two tangent lines to the circle that each has slope – \(\frac{1}{2}\).
Answer:
→ What is the center of the circle? The radius of the circle?
The center is (3, 5), and the radius is \(\sqrt{20}\).
→ If the tangent lines are to have a slope of – \(\frac{1}{2}\), what must be the slope of the radii to those tangent lines? Why?
The slope of each radius must be 2. A tangent is perpendicular to the radius at the point of tangency. Since the tangent lines must have slopes of – \(\frac{1}{2}\), the radii must have slopes of 2, the negative reciprocal of – \(\frac{1}{2}\).
→ Label the center O. We need to find a point A(x, y) on the circle with a slope of 2. We have
\(\frac{y – 5}{x – 3}\) = 2 and (x – 3)2 + (y – 5)2 = 20. Since y – 5 = 2(x – 3), then (y – 5)2 = 4(x – 3)2.
Substituting into the equation for the circle results in (x – 3)2 + 4(x – 3)2 = 20.
At this point, ask students to solve the equation for x and call on volunteers to share their results.
Ask if students noticed that using the distributive property made solving the equation easier.
(x – 3)2 (1 + 4) = 20
(x – 3)2 = 4
x – 3 = 2 or x – 3 = – 2
x = 5, 1
→ As expected, there are two possible values for x, 1 and 5. Why are two values expected?
There should be two lines tangent to a circle for any given slope.
→ What are the coordinates of the points of tangency? How can you determine the y – coordinates?
(1, 1) and (5, 9); it is easiest to find the y – coordinate by plugging each x – coordinate into the slope formula above (\(\frac{y – 5}{x – 3}\) = 2)
→ How can we verify that these two points lie on the circle?
Substituting the coordinates into the equation given for the circle proves that they, in fact, do lie on the circle.
→ How can we find the equations of these tangent lines? What are the equations?
We know both the slope and a point on each of the two tangent lines, so we can use the point – slope formula. The two equations are y – 1 = – \(\frac{1}{2}\)(x – 1) and y – 9 = – \(\frac{1}{2}\)(x – 5).
Example 2
Refer to the diagram below.
Let p > 1. What is the equation of the tangent line to the circle x2 + y2 = 1 through the point (p, 0) on the x – axis with a point of tangency in the upper half – plane?
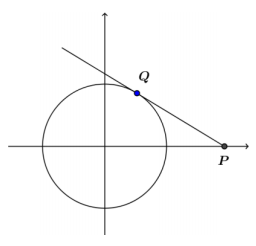
Answer:
→ Use Q(x, y)as the point of tangency, as shown in the diagram provided. Label the center as O(0, 0). What do we know about segments OQ and PQ?
They are perpendicular.
Write an equation that considers this.
\(\frac{y}{x}\) = \(\frac{p – x}{y – 0}\), giving x(p – x) – y2 = 0, or x2 – xp + y2 = 0.
Combine the two equations to find an expression for x.
Since x2 + y2 = 1, we get 1 – xp = 0, or x = \(\frac{1}{p}\).
Use the expression for x to find an expression for y.
y = \(\), which simplifies to y = \(\frac{1}{p}\) \(\sqrt{p^{2} – 1}\).
What are the coordinates of the point Q (the point of tangency)?
(\(\frac{1}{p}\), \(\frac{1}{p}\) \(\sqrt{p^{2} – 1}\))
What is the slope of \(\overline{O Q}\) in terms of p?
\(\sqrt{p^{2} – 1}\)
What is the slope of \(\overline{Q P}\) in terms of p?
\( – \frac{1}{\sqrt{p^{2} – 1}} = \frac{\sqrt{p^{2} – 1}}{1 – p^{2}}\)
What is the equation of line QP?
y = \(\frac{\sqrt{p^{2} – 1}}{1 – p^{2}}\)(x – p)
Eureka Math Geometry Module 5 Lesson 19 Exercise Answer Key
Opening Exercise
A circle of radius 5 passes through points A( – 3, 3) and B(3, 1).
a. What is the special name for segment AB?
Answer:
Segment AB is called a chord.
b. How many circles can be drawn that meet the given criteria? Explain how you know.
Answer:
Two circles of radius 5 pass through points A and B. Two distinct circles, at most, can have two points in common.
c. What is the slope of \(\overline{A B}\)?
Answer:
The slope of \(\overline{A B}\) is – \(\frac{1}{3}\).
d. Find the midpoint of \(\overline{A B}\).
Answer:
The midpoint of \(\overline{A B}\) is (0, 2).
e. Find the equation of the line containing a diameter of the given circle perpendicular to (AB) ̅.
Answer:
y – 2 = 3(x – 0)
f. Is there more than one answer possible for part (e)?
Answer:
Although two circles may be drawn that meet the given criteria, the diameters of both lie on the line perpendicular to (AB) ̅. That line is the perpendicular bisector of \(\overline{A B}\).
Exercise 1.
Consider the circle with equation (x – 4)2 + (y – 5)2 = 20. Find the equations of two tangent lines to the circle that each has slope 2.
Answer:
Use a point (x, y) and the coordinates of the center, (4, 5), to find the coordinates of the endpoints of the radii that are perpendicular to the tangent lines:
\(\frac{y – 5}{x – 4}\) = – \(\frac{1}{2}\)
(y – 5) = – \(\frac{1}{2}\)(x – 4)
Use the last step to write one variable in terms of another in order to substitute into the equation of the circle: (y – 5)2 = [ – \(\frac{1}{2}\) (x – 4)]2
(y – 5)2 = \(\frac{1}{4}\) (x – 4)2
Substitute: (x – 4)2 + \(\frac{1}{4}\) (x – 4)2 = 20
5/4 (x – 4)2 = 20
x(x – 8) = 0
x = 8, 0
The x – coordinates of the points of tangency are x = 8, 0.
Find the corresponding y – coordinates of the points of tangency:
\(\frac{y – 5}{(8) – 4}\) = – \(\frac{1}{2}\)
y = 3
\(\frac{y – 5}{(0) – 4}\) = – \(\frac{1}{2}\)
y = 7
The coordinates of the points of tangency: (8, 3) and (0, 7)
Use the determined points of tangency with the provided slope of 2 to write the equations for the tangent lines: y – 7 = 2(x – 0) and y – 3 = 2(x – 8)
Exercises 2–4
Exercise 2.
Use the same diagram from Example 2 above, but label the point of tangency in the lower half – plane as Q’.
a. What are the coordinates of Q^’?
Answer:
(\(\frac{1}{p}\), – \(\frac{1}{p}\) \(\sqrt{p^{2} – 1}\))
b. What is the slope of (OQ’) ̅?
Answer:
– \(\sqrt{p^{2} – 1}\)
c. What is the slope of (Q’P) ̅?
Answer:
\(\frac{\sqrt{p^{2} – 1}}{p^{2} – 1}\)
d. Find the equation of the second tangent line to the circle through (p, 0).
Answer:
y = \(\frac{\sqrt{p^{2} – 1}}{p^{2} – 1}\) (x – p)
Exercise 3.
Show that a circle with equation (x – 2)2 + (y + 3)2 = 160 has two tangent lines with equations y + 15 = \(\frac{1}{3}\)(x – 6) and y – 9 = \(\frac{1}{3}\) (x + 2).
Answer:
Assume that the circle has the tangent lines given by the equations above. Then, the tangent lines have slope \(\frac{1}{3}\), and the slope of the radius to those lines must be – 3. If we can show that the points (6, – 15) and ( – 2, 9) are on the circle, and that the slope of the radius to the tangent lines is – 3, then we will have shown that the given circle has the two tangent lines given.
(6 – 2)2 + ( – 15 + 3)2 = 42 + ( – 12)2
= 160
( – 2 – 2)2 + (9 + 3)2 = ( – 4)2 + 122
= 160
Since both points satisfy the equation, then the points (6, – 15) and ( – 2, 9) are on the circle.
m = \(\frac{ – 15 – ( – 3)}{6 – 2}\) = – \(\frac{12}{4}\) = – 3
m = \(\frac{9 – ( – 3)}{ – 2 – 2}\) = – \(\frac{12}{4}\) = – 3
The slope of the radius is – 3.
Exercise 4.
Could a circle given by the equation (x – 5)2 + (y – 1)2 = 25 have tangent lines given by the equations y – 4 = \(\frac{4}{3}\)(x – 1) and y – 5 = \(\frac{3}{4}\)(x – 8)? Explain how you know.
Answer:
Though the points (1, 4) and (8, 5) are on the circle, the given equations cannot represent tangent lines. For the equation y – 4 = \(\frac{4}{3}\) (x – 1), the slope of the tangent line is \(\frac{4}{3}\). To be tangent, the slope of the radius must be – \(\frac{3}{4}\), but the slope of the radius is \(\frac{3}{4}\); therefore, the equation does not represent a tangent line. Similarly, for the second equation, the slope is \(\frac{3}{4}\); to be tangent to the circle, the radius must have slope – \(\frac{4}{3}\), but the slope of the radius is \(\frac{4}{3}\). Neither of the given equations represents lines that are tangent to the circle.
Eureka Math Geometry Module 5 Lesson 19 Problem Set Answer Key
Question 1.
Consider the circle (x – 1)2 + (y – 2)2 = 16. There are two lines tangent to this circle having a slope of 0.
a. Find the coordinates of the points of tangency.
Answer:
(1, 6) and (1, – 2)
b. Find the equations of the two tangent lines.
Answer:
y = 6 and y = – 2
Question 2.
Consider the circle x2 – 4x + y2 + 10y + 13 = 0. There are two lines tangent to this circle having a slope of \(\frac{2}{3}\).
a. Find the coordinates of the two points of tangency.
Answer:
(\(\frac{ – 8 \sqrt{13} + 26}{13}\), \(\frac{12 \sqrt{13} – 65}{13}\)) and (\(\frac{8 \sqrt{13} + 26}{13}\), \(\frac{ – 12 \sqrt{13} – 65}{13}\)), or approximately ( – 0.2, – 1.7) and (4.2, – 8.3)
b. Find the equations of the two tangent lines.
Answer:
y – \(\frac{12 \sqrt{13} – 65}{13}\) = \(\frac{2}{3}\) (x + \(\frac{8 \sqrt{13} + 26}{13}\)) and y + \(\frac{12 \sqrt{13} – 65}{13}\) = \(\frac{2}{3}\) (x – \(\frac{8 \sqrt{13} + 26}{13}\)), or approximately
y + 1.7 = \(\frac{2}{3}\)(x + 0.2) and y + 8.3 = \(\frac{2}{3}\)(x – 4.2)
Question 3.
What are the coordinates of the points of tangency of the two tangent lines through the point (1, 1) each tangent to the circle x2 + y2 = 1?
Answer:
(0, 1) and (1, 0)
Question 4.
What are the coordinates of the points of tangency of the two tangent lines through the point ( – 1, – 1) each tangent to the circle x2 + y2 = 1?
Answer:
(0, – 1) and ( – 1, 0)
Question 5.
What is the equation of the tangent line to the circle x2 + y2 = 1 through the point (6, 0)?
Answer:
y = – \(\frac{\sqrt{35}}{35}\)(x – 6)
Question 6.
D’Andre said that a circle with equation (x – 2)2 + (y – 7)2 = 13 has a tangent line represented by the equation y – 5 = – \(\frac{3}{2}\) (x + 1). Is he correct? Explain.
Answer:
Yes, D’Andre is correct. The point ( – 1, 5) is on the circle, and the slopes are negative reciprocals.
Question 7.
Kamal gives the following proof that y – 1 = \(\frac{8}{9}\)(x + 10) is the equation of a line that is tangent to a circle given by
(x + 1)2 + (y – 9)2 = 145.
The circle has center ( – 1, 9) and radius 12.04. The point ( – 10, 1) is on the circle because
( – 10 + 1)2 + (1 – 9)2 = ( – 9)2 + ( – 8)2 = 145.
The slope of the radius is (9 – 1)/( – 1 + 10) = \(\frac{8}{9}\); therefore, the equation of the tangent line is y – 1 = \(\frac{8}{9}\) (x + 10).
a. Kerry said that Kamal has made an error. What was Kamal’s error? Explain what he did wrong.
Answer:
Kamal used the slope of the radius as the slope of the tangent line. To be tangent, the slopes must be negative reciprocals of one another, not the same.
b. What should the equation for the tangent line be?
Answer:
y – 1 = – \(\frac{9}{8}\)(x + 10)
Question 8.
Describe a similarity transformation that maps a circle given by x2 + 6x + y2 – 2y = 71 to a circle of radius 3 that is tangent to both axes in the first quadrant.
Answer:
The given circle has center ( – 3, 1) and radius 9. A circle that is tangent to both axes in the first quadrant with radius 3 must have a center at (3, 3). Then, a translation of x2 + 6x + y2 – 2y = 71 along a vector from ( – 3, 1) to (3, 3), and a dilation by a scale factor of \(\frac{1}{3}\) from the center (3, 3) will map circle x2 + 6x + y2 – 2y = 71 onto the circle in the first quadrant with radius 3.
Eureka Math Geometry Module 5 Lesson 19 Exit Ticket Answer Key
Consider the circle (x + 2)2 + (y – 3)2 = 9. There are two lines tangent to this circle having a slope of – 1.
Question 1.
Find the coordinates of the two points of tangency.
Answer:
(\(\frac{3 \sqrt{2} – 4}{2}\), \(\frac{3 \sqrt{2} + 6}{2}\)) and (\(\frac{ – 3 \sqrt{2} – 4}{2}\), \(\frac{ – 3 \sqrt{2} + 6}{2}\)), or approximately (0.12, 5.12) and ( – 4.12, 0.88)
Question 2.
Find the equations of the two tangent lines.
Answer:
y – \(\frac{3 \sqrt{2} + 6}{2}\) = – (x – \(\frac{3 \sqrt{2} – 4}{2}\)) and y – \(\frac{ – 3 \sqrt{2} + 6}{2}\) = – (x – \(\frac{ – 3 \sqrt{2} – 4}{2}\)), or approximately y – 5.12 = – (x – 0.12) and y – 0.88 = – (x + 4.12)