Engage NY Eureka Math 4th Grade Module 5 Lesson 28 Answer Key
Eureka Math Grade 4 Module 5 Lesson 28 Problem Set Answer Key
Question 1.
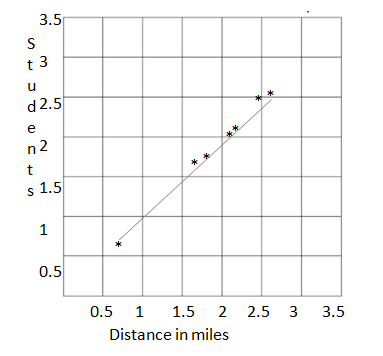
The chart to the right shows the distance fourth graders in Ms. Smith’s class were able to run before stopping for a rest. Create a line plot to display the data in the table.
| Student | Distance (in miles) |
| Joe | 2 \(\frac{1}{2}\) |
| Arianna | 1 \(\frac{3}{4}\) |
| Bobbi | 2 \(\frac{1}{8}\) |
| Morgan | 1 \(\frac{5}{8}\) |
| Jack | 2 \(\frac{5}{8}\) |
| Saisha | 2 \(\frac{1}{4}\) |
| Tyler | 2 \(\frac{2}{4}\) |
| Jenny | \(\frac{5}{8}\) |
| Anson | 2 \(\frac{2}{8}\) |
| Chandra | 2 \(\frac{4}{8}\) |
Answer:
Joe : 2(1/2) = 5/2.
Explanation:
In the above-given question,
given that,
2(1/2).
2 x 2 = 4.
4 +1 = 5.
5/2 = 2.5.
2(1/2) = 2.5.
Answer:
Arianna : 1(3/4) = 7/4.
Explanation:
In the above-given question,
given that,
1(3/4).
1 x 4 = 4.
4 +3 = 7.
7/4 = 1.75.
1(3/4) = 1.75.
Answer:
Bobbi : 2(1/8) = 17/8.
Explanation:
In the above-given question,
given that,
2(1/8).
8 x 2 = 16.
16 +1 = 17.
17/8 = 2.125.
2(1/8) = 2.125.
Answer:
Morgan : 1(5/8) = 13/8.
Explanation:
In the above-given question,
given that,
1(5/8).
1 x 8 = 8.
8 +5 = 13.
13/8 = 1.625.
1(5/8) = 1.625.
Answer:
Jack : 2(5/8) = 21/8.
Explanation:
In the above-given question,
given that,
2(5/8).
8 x 2 = 16.
16 +5 = 21.
21/8 = 2.6.
2(5/8) = 2.6.
Answer:
Saisha : 2(1/4) = 7/4.
Explanation:
In the above-given question,
given that,
2(1/4).
2 x 4 = 8.
8 + 1 = 9.
9/4 = 2.25.
2(1/4) = 2.25.
Answer:
Tyler : 2(2/4) = 10/4.
Explanation:
In the above-given question,
given that,
2(2/4).
2 x 4 = 8.
8 +2 = 10.
10/4 = 2.5.
2(2/4) = 2.5.
Answer:
Jenny : (5/8).
Explanation:
In the above-given question,
given that,
5/8.
5/8 = 0.625.
Answer:
Anson : 2(2/8) = 18/8.
Explanation:
In the above-given question,
given that,
2(2/8).
8 x 2 = 16.
16 +2 = 18.
18/8 = 2.25.
2(2/8) = 2.25.
Answer:
Chandra : 2(4/8) = 20/8.
Explanation:
In the above-given question,
given that,
2(4/8).
8 x 2 = 16.
16 +4 = 20.
20/8 = 2.5.
2(4/8) = 2.5.
Question 2.
Solve each problem.
a. Who ran a mile farther than Jenny?
Answer:
Morgan ran a mile farther than Jenny = 1.625.
Explanation:
In the above-given question,
given that,
5/8.
5/8 = 0.625.
0.625 + 1.
1.625.
so morgan ran a mile more than jenny.
b. Who ran a mile less than Jack?
Answer:
Morgan ran a mile less than Jack.
Explanation:
In the above-given question,
given that,
Jack: 2(5/8).
16 + 5/8.
21/8 = 2.6.
2.6 – 1.6 = 1.6.
so morgan ran a mile less than jack.
c. Two students ran exactly 2\(\frac{1}{4}\) miles. Identify the students. How many quarter miles did each student run?
Answer:
Joe and Saisha exactly ran exactly.
Explanation:
In the above-given question,
given that,
2(1/4).
4 x 2 = 8.
8 + 1/4 = 9/4.
9/4 = 2.25.
Joe = 2.25.
Saisha = 2.25.
d. What is the difference, in miles, between the longest and shortest distance run?
Answer:
The difference in miles between the longest and shortest distance run = 1.875 miles.
Explanation:
In the above-given question,
given that,
The longest distance run is Joe and Chandra.
the shortest distance run is Jenny.
Joe and Chandra = 2.5.
Jenny = 0.625.
2.5 – 0.625 = 1.875 miles.
e. Compare the distances run by Arianna and Morgan using >, <, or =.
Answer:
Arianna > Morgan.
Explanation:
In the above-given question,
given that,
the distances run by Arianna and Morgan is
Arianna = 1.75 miles.
Morgan = 1.625.
1.75 > 1.625.
Arianna is greater than Morgan.
f. Ms. Smith ran twice as far as Jenny. How far did Ms. Smith run? Write her distance as a mixed number.
Answer:
Ms. smith ran as far as Jenny = 1.25 miles.
Explanation:
In the above-given question,
given that,
Ms. Smith ran twice as far as Jenny.
Jenny run = 0.625.
smith = 1.25 miles.
0.625 + 0.625 = 1.25.
g. Mr. Reynolds ran 1\(\frac{3}{10}\) miles. Use >, <, or = to compare the distance Mr. Reynolds ran to the distance that Ms. Smith ran. Who ran farther?
Answer:
Mr. Reynold > Ms. Smith.
Explanation:
In the above-given question,
given that,
Mr. Reynolds ran 1(3/10) miles.
1(3/10) = 10 x 1.
10 x 1 = 10.
10 + 3/10.
13/10 = 1.3.
1.3 > 1.25.
Question 3.
Using the information in the table and on the line plot, develop and write a question similar to those above. Solve, and then ask your partner to solve. Did you solve in the same way? Did you get the same answer?
Answer:
Yes, I get the same answer.
Explanation:
In the above-given question,
given that,
my partner also draws the same.
so we both solved in the same way.
so I get the same answer.
Eureka Math Grade 4 Module 5 Lesson 28 Exit Ticket Answer Key
Mr. O’Neil asked his students to record the length of time they read over the weekend. The times are listed in the table.
| Student | Length of time (in hours) |
| Robin | \(\frac{1}{2}\) |
| Bill | 1 |
| Katrina | \(\frac{3}{4}\) |
| Kelly | 1 \(\frac{3}{4}\) |
| Mary | 1 \(\frac{1}{2}\) |
| Gail | 2\(\frac{1}{4}\) |
| Scott | 1\(\frac{3}{4}\) |
| Ben | 2\(\frac{2}{4}\) |
Question 1.
At the bottom of the page, make a line plot of the data.
Answer:
Robin: 1/2 = 0.5.
Explanation:
In the above-given question,
given that,
Robin = 1/2.
1/2 = 0.5.
Answer:
Bill: 1.
Explanation:
In the above-given question,
given that,
Bill read over the weekend.
1.
Answer:
Katrina: 3/4.
Explanation:
In the above-given question,
given that,
Katrina read over the weekend.
3/4 = 0.75.
Answer:
Kelly: 1(3/4).
Explanation:
In the above-given question,
given that,
Kelly read over the weekend.
1(3/4) = 4 x 1.
4 + 3/4 = 7/4.
7/4 = 1.75.
Answer:
Mary: 1(1/2).
Explanation:
In the above-given question,
given that,
Mary read over the weekend.
1(1/2) = 2 x 1.
2 + 1/2 = 3/2.
3/2 = 1.5.
Answer:
Gail: 2(1/4).
Explanation:
In the above-given question,
given that,
Mary read over the weekend.
2(1/4) = 2 x 4.
8 + 1/4 = 9/4.
9/4 = 2.25.
Answer:
Scott: 1(3/4).
Explanation:
In the above-given question,
given that,
Mary read over the weekend.
1(3/4) = 4 x 1.
4 + 3/4 = 7/4.
7/4 = 1.75.
Answer:
Ben: 2(2/4).
Explanation:
In the above-given question,
given that,
Mary read over the weekend.
2(2/4) = 2 x 4.
8 + 2/4 = 10/4.
10/4 = 2.5.
Question 2.
One of the students read \(\frac{3}{4}\) hour on Friday, \(\frac{3}{4}\) hour on Saturday, and \(\frac{3}{4}\) hour on Sunday. How many hours did that student read over the weekend? Name that student.
Answer:
Katrina, Scott, and Kelly.
Explanation:
In the above-given question,
given that,
Katrina read 3/4 hours on Friday.
3/4 = 0.75.
Kelly read 3/4 hours on Saturday.
Scott read 3/4 hours on Sunday.
Eureka Math Grade 4 Module 5 Lesson 28 Homework Answer Key
Question 1.
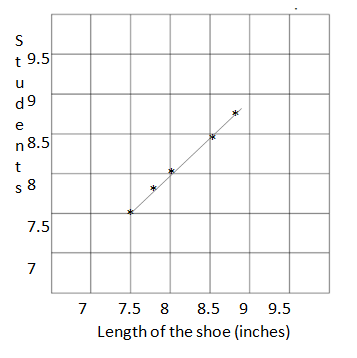
A group of students measured the lengths of their shoes. The measurements are shown in the table. Make a line plot to display the data.
|
Students |
Length of shoe (in inches) |
| Collin | 8\(\frac{1}{2}\) |
| Dickon | 7\(\frac{3}{4}\) |
| Ben | 7\(\frac{1}{2}\) |
| Martha | 7\(\frac{3}{4}\) |
| Lilias | 8 |
| Susan | 8\(\frac{1}{2}\) |
| Frances | 7\(\frac{3}{4}\) |
| Mary | 8\(\frac{3}{4}\) |
Answer:
Collin: 8(1/2).
Explanation:
In the above-given question,
given that,
The length of the Collin shoes.
8(1/2) = 2 x 8.
16 + 1/2.
17/2 = 8.5.
Answer:
Dickon: 7(3/4).
Explanation:
In the above-given question,
given that,
The length of the Dickon shoes.
7(3/4) = 7 x 4.
28 + 3/4.
31/4 = 7.75.
Answer:
Ben: 7(1/2).
Explanation:
In the above-given question,
given that,
The length of the Ben shoes.
7(1/2) = 2 x 7.
14 + 1/2.
15/2 = 7.5.
Answer:
Martha: 7(3/4).
Explanation:
In the above-given question,
given that,
The length of the Martha shoes.
7(3/4) = 7 x 4.
28 + 3/4.
31/4 = 7.75.
Answer:
Lilias: 8.
Explanation:
In the above-given question,
given that,
The length of the Lilias shoes.
8.
Answer:
Susan: 8(1/2).
Explanation:
In the above-given question,
given that,
The length of the Susan shoes.
8(1/2) = 2 x 8.
16 + 1/2.
17/2 = 8.5.
Answer:
Frances: 7(3/4).
Explanation:
In the above-given question,
given that,
The length of the Frances shoes.
7(3/4) = 7 x 4.
28 + 3/4.
31/4 = 7.75.
Answer:
Mary: 8(3/4).
Explanation:
In the above-given question,
given that,
The length of the Mary shoes.
8(3/4) = 4 x 8.
32 + 3/4.
35/4 = 8.75.
Question 2.
Solve each problem.
a. Who has a shoe length 1 inch longer than Dickon’s?
Answer:
The shoe length 1-inch longer than Dickon’s is Mary.
Explanation:
In the above-given question,
given that,
The shoe length of Mary = 8(3/4).
8 x 4 = 32.
32 + 3/4 = 35/4.
35/4 = 8.75.
8.75 – 1 = 7.75.
b. Who has a shoe length 1 inch shorter than Susan’s?
Answer:
The shoe length 1-inch is shorter than Susan’s is Ben.
Explanation:
In the above-given question,
given that,
The shoe length of Ben = 7(1/2).
7 x 2 = 14.
14 + 1/2 = 15/2.
15/2 = 7.5.
7.5 + 1 = 8.5.
c. How many quarter inches long is Martha’s shoe length?
Answer:
The length of Martha’s Shoe length = 7 quarter inches.
Explanation:
In the above-given question,
given that,
The length of Martha’s Shoe = 7(3/4).
1 quarter-inch = 3/4.
7(3/4) = 7 quarter inches.
d. What is the difference, in inches, between Lilias’s and Martha’s shoe lengths?
Answer:
The difference in inches between the Lilias’s and Martha’s shoe lengths = 0.25 inches.
Explanation:
In the above-given question,
given that,
Lilias’s shoe length = 8.
Martha’s shoe length = 7.75.
8 – 7.75 = 0.25 inches.
e. Compare the shoe length of Ben and Frances using >, <, or =.
Answer:
France > Ben.
Explanation:
In the above-given question,
given that,
Shoe length of Ben = 7.5.
Shoe length of France = 7.75.
7.7 > 7.5.
so Ben is greater than France.
f. How many students had shoes that measured less than 8 inches?
Answer:
The students who measured less than 8 inches = 4.
Explanation:
In the above-given question,
given that,
The students who measured less than 8 inches is 4.
they are Dickon = 7.75.
Ben = 7.5.
Martha = 7.75.
Frances = 7.75.
g. How many students measured the length of their shoes?
Answer:
The number of students measured the length of their shoes = 8.
Explanation:
In the above-given question,
given that,
the 8 students measured their shoes.
the students are Collin, Dickon, Ben, Martha, Lilias, Susan, Frances, and Mary.
h. Mr. Jones’s shoe length was \(\frac{25}{2}\) inches. Use >, <, or = to compare the length of Mr. Jones’s shoe to the length of the longest student shoe length. Who had the longer shoe?
Answer:
Mary < Mr. Jones’s.
Explanation:
In the above-given question,
given that,
Mr. Jone’s shoe length was 25/2 inches.
25/2 = 12.5.
Mary shoe length = 8.75.
8.75 < 12.5.
Question 3.
Using the information in the table and on the line plot, write a question you could solve by using the line plot. Solve.
Answer:
The length of the shoe length increases.
Explanation:
In the above-given question,
given that,
The length of the shoe increases.
the length increases by 0.5 in.