Engage NY Eureka Math 6th Grade Module 3 Lesson 1 Answer Key
Eureka Math Grade 6 Module 3 Lesson 1 Exercise Answer Key
Complete the diagrams. Count by ones to label the number lines.

Exercise 1.
Plot your point on both number lines.
Answer:
Answers may vary.
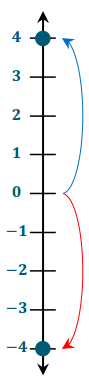
Exercise 2.
Show and explain how to find the opposite of your number on both number lines.
Answer:
In this example, the number chosen was – 4. So – 4 is the first number plotted, and the opposite is 4. Horizontal Number Line: I found my point by starting at zero and counting four units to the left to end on – 4. Then, to find the opposite of my number, I started on zero and counted to the right four units to end on 4. Vertical Number Line: I found my point by starting at zero and counting four units down to end on – 4. I found the opposite of my number by starting at zero and counting four units up to end on 4.
Exercise 3.
Mark the opposite on both number lines.
Answer:
Answers may vary.
Exercise 4.
Choose a group representative to place the opposite number on the class number lines.
Answer:
Exercise 5.
Which group had the opposite of the number on your index card?
Answer:
Answers may vary. Jackie’s group had the opposite of the number on my index card. They had 4.
Eureka Math Grade 6 Module 3 Lesson 1 Problem Set Answer Key
Question 1.
Draw a number line, and create a scale for the number line in order to plot the points – 2, 4, and 6.
a. Graph each point and its opposite on the number line.
Answer:

b. Explain how you found the opposite of each point.
Answer:
To graph each point, I started at zero and moved right or left based on the sign and number (to the right for a positive number and to the left for a negative number). To graph the opposites, I started at zero, but this time I moved in the opposite direction the same number of times.
Question 2.
Carlos uses a vertical number line to graph the points – 4, – 2, 3, and 4. He notices that – 4 is closer to zero than – 2. He is not sure about his diagram. Use what you know about a vertical number line to determine if Carlos made a mistake or not. Support your explanation with a number line diagram.
Answer:
Carlos made a mistake because – 4 is less than – 2, so it should be farther down the number line. Starting at zero, negative numbers decrease as we look farther below zero. So, – 2 lies before – 4 on a number line since – 2 is 2 units below zero and – 4 is 4 units below zero.
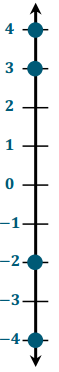
Question 3.
Create a scale in order to graph the numbers – 12 through 12 on a number line. What does each tick mark represent?
Answer:
Each tick mark represents 1 unit.

Question 4.
Choose an integer between – 5 and – 10. Label it R on the number line created in Problem 3, and complete the following tasks.
Answers may vary. Refer to the number line above for sample student work. – 6, – 7, – 8, or – 9
a. What is the opposite of R? Label it Q.
Answer:
Answers will vary. 6
b. State a positive integer greater than Q. Label it T.
Answer:
Answers will vary. 11
c. State a negative integer greater than R. Label it S.
Answer:
Answers will vary. – 3
d. State a negative integer less than R. Label it U.
Answer:
Answers will vary. 9
e. State an integer between R and Q. Label it V.
Answer:
Answers will vary. 2
Question 5.
Will the opposite of a positive number always, sometimes, or never be a positive number? Explain your reasoning.
Answer:
The opposite of a positive number will never be a positive number. For two nonzero numbers to be opposites, zero has to be in between both numbers, and the distance from zero to one number has to equal the distance between zero and the other number.
Question 6.
Will the opposite of zero always, sometimes, or never be zero? Explain your reasoning.
Answer:
The opposite of zero will always be zero because zero is its own opposite.
Question 7.
Will the opposite of a number always, sometimes, or never be greater than the number itself? Explain your reasoning. Provide an example to support your reasoning.
Answer:
The opposite of a number will sometimes be greater than the number itself because it depends on the given number. For example, if the number given is – 6, then the opposite is 6, which is greater than – 6. If the number given is 5, then the opposite is – 5, which is not greater than 5. If the number given is 0, then the opposite is 0, which is never greater than itself.
Eureka Math Grade 6 Module 3 Lesson 1 Exit Ticket Answer Key
Question 1.
Draw a number line, and create a scale for the number line in order to plot the points —2, 4, and 6.
a. Graph each point and its opposite on the number line.

Answer:
Answers will vary. One possible answer is a: – 4; b: – 1; C: 1; d: 4.
Question 2.
Below is a list of numbers in order from least to greatest. Use what you know about the number line to complete the list of numbers by filling in the blanks with the missing integers.
– 6, – 5, ________, – 3, – 2, – 1, ________, 1, 2, _______, 4, ________, 6
Answer:
– 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6
Question 3.
Complete the number line scale. Explain and show how to find 2 and the opposite of 2 on a number line.
Answer:
I would start at zero and move 2 units to the left to locate the number – 2 on the number line. So, to locate 2, 1 would start at zero and move 2 units to the right (the opposite direction).

Eureka Math Grade 6 Module 3 Lesson 1 Exploratory Challenge Answer Key
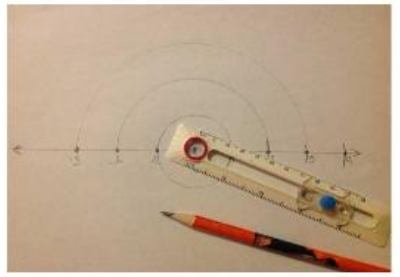
Exploratory Challenge: Constructing the Number Line
Answer:
The purpose of this exercise is to let students construct the number line (positive and negative numbers and zero) using a compass.
Have students draw a line, place a point on the line, and label it 0.
Have students use the compass to locate and label the next point 1, thus creating the scale. Students continue to locate other whole numbers to the right of zero using the same unit measure.
Using the same process, have students locate the opposites of the whole numbers. Have students label the first point to the left of zero – 1.
Introduce to the class the definition of the opposite of a number.
Sample student work is shown below.