Engage NY Eureka Math Grade 6 Module 5 Lesson 4 Answer Key
Eureka Math Grade 6 Module 5 Lesson 4 Exercise Answer Key
Opening Exercise:
Draw and label the altitude of each triangle below.
Question a.
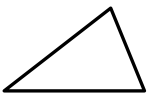
Answer:
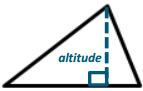
Question b.
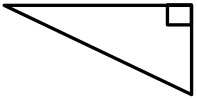
Answer:
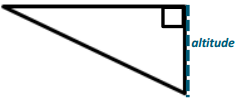
Question c.
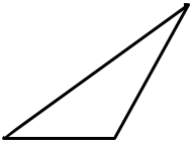
Answer:
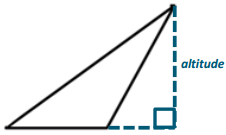
Exploratory Challenge/Exercises 1 – 5:
Question 1.
Use rectangle X and the triangle with the altitude inside (triangle X) to show that the area formula for the triangle is A = \(\frac{1}{2}\) × base × height.
a. Step One: Find the area of rectangle X.
Answer:
A = 3 in. × 2.5 in. = 7.5 in2
b. Step Two: What is half the area of rectangle X?
Answer:
Half of the area of the rectangle is 7.5 in2 ÷ 2= 3.75 in2
c. Step Three: Prove, by decomposing triangle X, that it is the same as half of rectangle X. Please glue your decomposed triangle onto a separate sheet of paper. Glue it into rectangle X. What conclusions can you make about the triangle’s area compared to the rectangle’s area?
Answer:
Because the triangle fits inside half of the rectangle, we know the triangle’s area is half of the rectangle’s area.
Question 2.
Use rectangle Y and the triangle with a side that ¡s the altitude (triangle Y) to show the area formula for the triangle is A = \(\frac{1}{2}\) × base × height.
a. Step One: Find the area of rectangle Y.
Answer:
A = 3 in. × 3 in. = 9 in2
b. Step Two: What is half the area of rectangle Y?
Answer:
Half the area of the rectangle is 9 in2 ÷ 2 = 4.5 in2.
c. Step Three: Prove, by decomposing triangle Y, that it is the same as half of rectangle Y. Please glue your decomposed triangle onto a separate sheet of paper. Glue it into rectangle Y. What conclusions can you make about the triangle’s area compared to the rectangle’s area?
Answer:
The right triangle also fits in exactly half of the rectangle, so the triangle’s area is • Students may struggle once again half the size of the rectangle’s area. with this step since they have yet to see an obtuse
Question 3.
Use rectangle Z and the triangle with the altitude outside (triangle Z) to show that the area angle. formula for the triangle is A = \(\frac{1}{2}\) × base × height.
a. Step One: Find the area of rectangle Z.
Answer:
A= 3 in. × 2.5 in.=7.5 in2
b. Step Two: What is half the area of rectangle Z?
Answer:
Half of the area of the rectangle is 7.5 in2 ÷2 = 3.75 in2.
c. Step Three: Prove, by decomposing triangle Z, that it is the same as half of rectangle Z. Please glue your decomposed triangle onto a separate sheet of paper. Glue it into rectangle Z. What conclusions can you make about the triangle’s area compared to the rectangle’s area?
Answer:
Similar to the other two triangles, when the altitude is outside the triangle, the area of the triangle is exactly half of the area of the rectangle.
Question 4.
When finding the area of a triangle, does it matter where the altitude is located?
Answer:
It does not matter where the altitude is located. To find the area of a triangle, the formula is always
A = \(\frac{1}{2}\) × base × height.
Question 5.
How can you determine which part of the triangle is the base and which is the height?
Answer:
The base and the height of any triangle form a right angle because the altitude is always perpendicular to the base.
Exercises 6 – 8:
Calculate the area of each triangle. Figures are not drawn to scale.
Question 6.
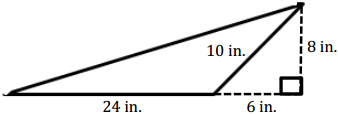
Answer:
A = \(\frac{1}{2}\) × (24 in.) (8 in.) = 96 in2
Question 7.
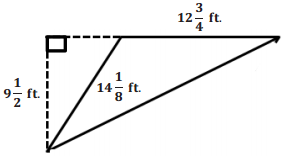
Answer:
![]()
Question 8.
Draw three triangles (acute, right, and obtuse) that have the same area. Explain how you know they have the same area.
Answer:
Answers will vary.
Eureka Math Grade 6 Module 5 Lesson 4 Problem Set Answer Key
Calculate the area of each figure below. Figures are not drawn to scale.
Question 1.
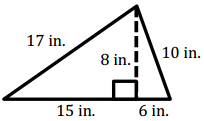
Answer:
A = \(\frac{1}{2}\) (21 in.) (8 in.) = 84 in2
Question 2.
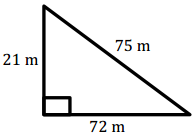
Answer:
A = \(\frac{1}{2}\) (72 m) (21 m) = 756 m2
Question 3.
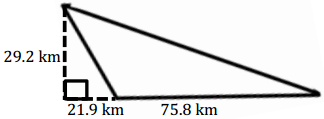
Answer:
A = \(\frac{1}{2}\) (75.8 km) (29.2 km) = 1,106.68 km2
Question 4.
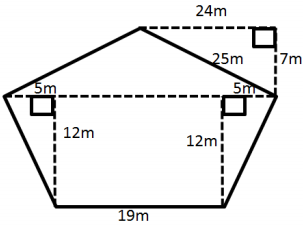
Answer:
A = \(\frac{1}{2}\) (5 m) (12 m) = 30 m2
A = \(\frac{1}{2}\) (7 m) (29 m) = 101.5 m2
A = (12 m) (19 m) = 228 m2
A = 30 m2 + 30 m2 + 101.5 m2 + 228 m2
A = 389.5 m2
Question 5.
The Andersons are going on a long sailing trip during the summer. However, one of the sails on their sailboat ripped, and they have to replace it. The sail is pictured below. If the sailboat sails are on sale for $2 per square foot, how much will the new sail cost?
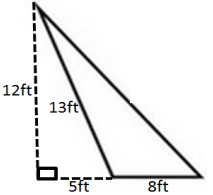
Answer:
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (8 ft.) (12 ft.)
= 48 ft2
\(\frac{2 \text { dollars }}{\mathrm{ft}^{2}}\) × 48 ft2 = 96 dollars(or $96)
The cost of the new sail is $96.
Question 6.
Darnell and Donovan are both trying to calculate the area of an obtuse triangle. Examine their calculations below.
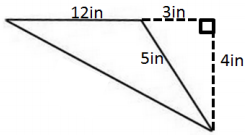
| Darnell’s Work | Donovan’s Work |
| A = \(\frac{1}{2}\) × 3 in. × 4 in.
A = 6 in2 |
A = \(\frac{1}{2}\) × 12 in. × 4 in.
A = 24 in2 |
Which student calculated the area correctly? Explain why the other student is not correct.
Answer:
Donovan calculated the area correctly. Although Darnell did use the altitude of the triangle, he used the length between the altitude and the base rather than the length of the actual base.
Question 7.
Russell calculated the area of the triangle below. His work is shown.
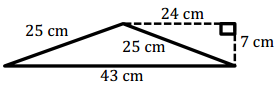
A = \(\frac{1}{2}\) bh
A = 150.5 cm2
Although Russell was told his work is correct, he had a hard time explaining why it is correct. Help Russell explain why his calculations are correct.
Answer:
The formula for the area of triangle is A = bit. Russell followed this formula because 7 cm is the height of the triangle, and 43 cm is the base of the triangle.
Question 8.
The larger triangle below has a base of 10.14 m; the gray triangle has an area of 40.325 m2.
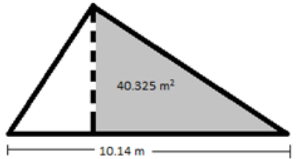
a. Determine the area of the larger triangle if it has a height of 12.2 m.
Answer:
A = \(\frac{1}{2}\) (10.14 m) (12.2 m)
= 61.854 m2
b. Let A be the area of the unshaded (white) triangle in square meters. Write and solve an equation to determine the value of A, using the areas of the larger triangle and the gray triangle.
Answer:
40.325m2 + A = 61.854m2
40.325m2 + A – 40.325 m2 = 61.854 m2 – 40.325 m2
A = 21.529 m2
Eureka Math Grade 6 Module 5 Lesson 4 Exit Ticket Answer Key
Find the area of each triangle. Figures are not drawn to scale.
Question 1.
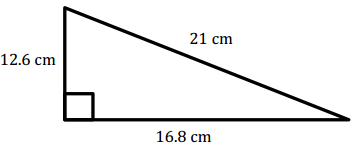
Answer:
A = \(\frac{1}{2}\) (12.6 cm) (16.8 cm) = 105.84 cm2
Question 2.
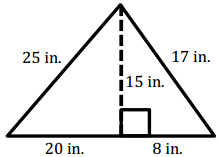
Answer:
A = \(\frac{1}{2}\) (28 in.) (15 in.) = 210 in2
Question 3.

Answer:
A = \(\frac{1}{2}\) (12 ft.) (21 ft.) = 126 ft2