Engage NY Eureka Math 7th Grade Module 1 Lesson 11 Answer Key
Eureka Math Grade 7 Module 1 Lesson 11 Example Answer Key
Example 1.
Who is Faster?
Answer:
During their last workout, Izzy ran 2\(\frac{1}{4}\) miles in 15 minutes, and her friend Julia ran 3\(\frac{3}{4}\) miles in 25 minutes. Each girl thought she was the faster runner. Based on their last run, which girl is correct? Use any approach to find the solution.
Tables:
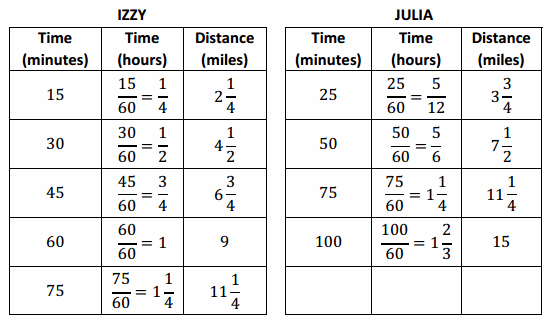
→ When looking at and comparing the tables, it appears that Julia went farther, so this would mean she ran faster. Is that assumption correct? Explain your reasoning.
→ By creating a table of equivalent ratios for each runner showing the elapsed time and corresponding distance ran, it may be possible to find a time or a distance that is common to both tables. It can then be determined if one girl had a greater distance for a given time or if one girl had less time for a given distance. In this case, at 75 minutes, both girls ran 11\(\frac{1}{4}\) miles, assuming they both ran at a constant speed.
→ How can we use the tables to determine the unit rate?
→ Since we assumed distance is proportional to time, the unit rate or constant of proportionality can be determined by dividing the distance by the time. When the time is in hours, then the unit rate is calculated in miles per hour, which is 9. If the time is in minutes, then the unit rate is calculated in miles per minute, which is \(\frac{3}{20}\).
→ Discuss: Some students may have chosen to calculate the unit rates for each of the girls. To calculate the unit rate for Izzy, students divided the distance ran, 2\(\frac{1}{4}\) , by the elapsed time, \(\frac{15}{60}\) , which has a unit rate of 9. To find the unit rate for Julia, students divided 3 \(\frac{3}{4}\) by \(\frac{25}{60}\) and arrived at a unit rate of 9, as well, leading students to conclude that neither girl was faster.
→ We all agree that the girls ran at the same rate; however, some members of the class identified the unit rate as 9 while others gave a unit rate of \(\frac{3}{20}\) . How can both groups of students be correct?
→ Time can be represented in minutes; however, in real-world contexts, most people are comfortable with distance measured by hours. It is easier for a person to visualize 9 miles per hour compared to \(\frac{3}{20}\) miles per minute, although it is an acceptable answer.
Equations:

→ What assumptions are made when using the formula d = rt in this problem?
→ We are assuming the distance is proportional to time, and that Izzy and Julia ran at a constant rate. This means they ran the same speed the entire time not slower at one point or faster at another.
Picture:
→ Some students may decide to draw a clock.
→ Possible student explanation:
For Izzy, every 15 minutes of running results in a distance of 2 \(\frac{1}{4}\) miles. Since the clock is divided into 15-minute intervals, I added the distance for each 15-minute interval until I reached 60 minutes. Julia’s rate is 3 \(\frac{3}{4}\) miles in 25 minutes, so I divided the clock into 25-minute intervals. Each of those 25-minute intervals represents 3 \(\frac{3}{4}\) miles. At 50 minutes, the distance represented is two times 3 \(\frac{3}{4}\) , or 7 \(\frac{1}{2}\) miles. To determine the distance ran in the last ten minutes, I needed to determine the distance for 5 minutes: 3 \(\frac{3}{4}\) ÷5 = \(\frac{3}{4}\) . Therefore, 3 \(\frac{3}{4}\) + 3 \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) = 9, or 9 miles per hour.
Total Distance for 1 hour
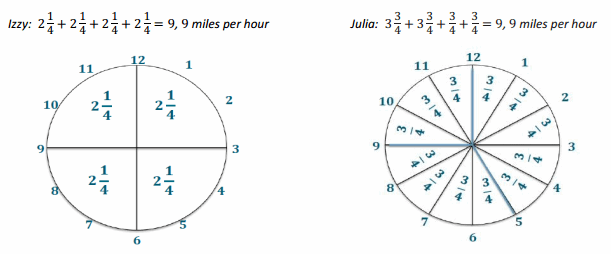
→ How do you find the value of a 5-minute time increment? What are you really finding?
→ To find the value of a 5-minute increment, you need to divide 3 \(\frac{3}{4}\) by 5 since 25 minutes is five 5-minute increments. This is finding the unit rate for a 5-minute increment.
→ Why were 5-minute time increments chosen?
→ 5-minute time increments were chosen for a few reasons. First, a clock can be separated into 5-minute intervals, so it may be easier to visualize what fractional part of an hour one has when given a 5-minute interval. Also, 5 is the greatest common factor of the two given times.
→ What if the times had been 24 and 32 minutes or 18 and 22 minutes? How would this affect the time increments?
→ If the times were 24 and 32 minutes, then the time increment would be 8-minute intervals. This is because 8 is the greatest common factor of 24 and 32.
→ If the times were 18 and 22 minutes, then the comparison should be broken into 2-minute intervals since the greatest common factor of 18 and 22 is 2.
Double Number Line Approach:
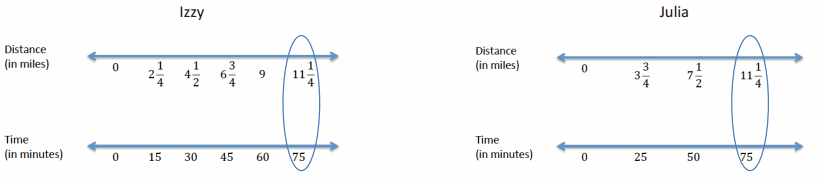
Example 2
Is Meredith Correct?
A turtle walks \(\frac{7}{8}\) of a mile in 50 minutes. What is the unit rate when the turtle’s speed is expressed in miles per hour?
a. To find the turtle’s unit rate, Meredith wrote the following complex fraction. Explain how the fraction \(\frac{5}{6}\) was obtained.
Answer:
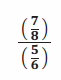
To determine the unit rate, Meredith divided the distance walked by the amount of time it took the turtle. Since the unit rate is expressed in miles per hour, 50 minutes needs to be converted to hours. Since 60 minutes is equal to 1 hour, 50 minutes can be written as \(\frac{50}{60}\) hours, or \(\frac{5}{6}\) hours.
→ How can we determine the unit rate? We need a denominator of 1 hour. Right now, the denominator is \(\frac{5}{6}\) hours.
→ We can multiply \(\frac{5}{6}\) by its multiplicative inverse \(\frac{6}{5}\) to determine a denominator of 1 hour.
→ Using this information, determine the unit rate in miles per hour.
b. Determine the unit rate when the turtle’s speed is expressed in miles per hour.
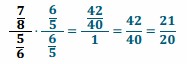
Answer:
The unit rate is \(\frac{21}{20}\) . The turtle’s speed is \(\frac{21}{20}\) mph.
Eureka Math Grade 7 Module 1 Lesson 11 Exercise Answer Key
Exercise 1.
For Anthony’s birthday, his mother is making cupcakes for his 12 friends at his daycare. The recipe calls for 3 \(\frac{1}{3}\) cups of flour. This recipe makes 2 \(\frac{1}{2}\) dozen cupcakes. Anthony’s mother has only 1 cup of flour. Is there enough flour for each of his friends to get a cupcake? Explain and show your work.
Answer:
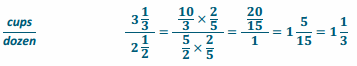
No, since Anthony has 12 friends, he would need 1 dozen cupcakes. This means you need to find the unit rate. Finding the unit rate tells us how much flour his mother needs for 1 dozen cupcakes. Upon finding the unit rate, Anthony’s mother would need 1 \(\frac{1}{3}\) cups of flour; therefore, she does not have enough flour to make cupcakes for all of his friends.
Exercise 2.
Sally is making a painting for which she is mixing red paint and blue paint. The table below shows the different mixtures being used.
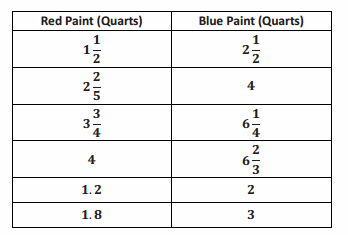
a. What is the unit rate for the values of the amount of blue paint to the amount of red paint?
Answer:
\(\frac{5}{3}\) = 1\(\frac{2}{3}\)
b. Is the amount of blue paint proportional to the amount of red paint?
Answer:
Yes. Blue paint is proportional to red paint because there exists a constant, \(\frac{5}{3}\) =1 \(\frac{2}{3}\) , such that when each amount of red paint is multiplied by the constant, the corresponding amount of blue paint is obtained.
c. Describe, in words, what the unit rate means in the context of this problem.
Answer:
For every 1 \(\frac{2}{3}\) quarts of blue paint, Sally must use 1 quart of red paint.
Eureka Math Grade 7 Module 1 Lesson 11 Problem Set Answer Key
Question 1.
Determine the quotient: 2 \(\frac{4}{7}\) ÷1 \(\frac{3}{6}\) .
Answer:
1\(\frac{5}{7}\)
Question 2.
One lap around a dirt track is \(\frac{1}{3}\) mile. It takes Bryce \(\frac{1}{9}\) hour to ride one lap. What is Bryce’s unit rate, in miles, around the track?
Answer:
3
Question 3.
Mr. Gengel wants to make a shelf with boards that are 1 \(\frac{1}{3}\) feet long. If he has an 18-foot board, how many pieces can he cut from the big board?
Answer:
13 \(\frac{1}{2}\) boards
Question 4.
The local bakery uses 1.75 cups of flour in each batch of cookies. The bakery used 5.25 cups of flour this morning.
a. How many batches of cookies did the bakery make?
Answer:
3 batches
b. If there are 5 dozen cookies in each batch, how many cookies did the bakery make?
Answer:
5(12) = 60
There are 60 cookies per batch.
60(3) = 180
So, the bakery made 180 cookies.
Question 5.
Jason eats 10 ounces of candy in 5 days.
a. How many pounds does he eat per day? (Recall: 16 ounces =1 pound)
Answer:
\(\frac{1}{8}\) lb. each day
b. How long will it take Jason to eat 1 pound of candy?
Answer:
8 days
Eureka Math Grade 7 Module 1 Lesson 11 Exit Ticket Answer Key
Which is the better buy? Show your work and explain your reasoning.
![]()
Answer:
![]()
2\(\frac{1}{2}\) lb. is the best buy because the price per pound is cheaper.