Engage NY Eureka Math 7th Grade Module 1 Lesson 7 Answer Key
Eureka Math Grade 7 Module 1 Lesson 7 Example Answer Key
Example 1.
National Forest Deer Population in Danger?
Wildlife conservationists are concerned that the deer population might not be constant across the National Forest. The scientists found that there were 144 deer in a 16-square-mile area of the forest. In another part of the forest, conservationists counted 117 deer in a 13-square-mile area. Yet a third conservationist counted 216 deer in a 24-square-mile plot of the forest. Do conservationists need to be worried?
a. Why does it matter if the deer population is not constant in a certain area of the National Forest?
Answer:
Have students generate as many theories as possible (e.g., food supply, overpopulation, damage to land).
b. What is the population density of deer per square mile?
Answer:
See table below.
Encourage students to make a chart to organize the data from the problem, and then explicitly model finding the constant of proportionality. Students have already found unit rate in earlier lessons but have not identified it as the constant of proportionality.
→ When we find the number of deer per 1 square mile, what is this called?
→ Unit rate.
→ When we look at the relationship between square miles and number of deer in the table below, how do we know if the relationship is proportional?
→ The square miles are always multiplied by the same value, 9 in this case.
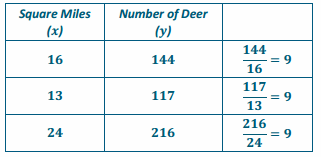
→ We call this constant (or same) value the constant of proportionality.
→ So, the number of deer per square mile is 9, and the constant of proportionality is 9. Is that a coincidence, or will the unit rate of \(\frac{y}{x}\) and the constant of proportionality always be the same?
Allow for comments or observations, but leave a lingering question for now.
→ We could add the unit rate to the table so that we have 1 square mile in the first column and 9 in the second column. (Add this to the table for students to see.) Does that help to guide your decision about the relationship between the unit rate of \(\frac{y}{x}\) and the constant of proportionality? We will see if your hypothesis remains true as we move through more examples.
The unit rate of deer per 1 square mile is 9.
Constant of Proportionality:
Answer:
k = 9
Explain the meaning of the constant of proportionality in this problem:
Answer:
There are 9 deer for every 1 square mile of forest.
c. Use the unit rate of deer per square mile (or \(\frac{y}{x}\)) to determine how many deer there are for every 207 square miles.
Answer:
9(207)=1,863
There are 1,863 deer for every 207 square miles.
d. Use the unit rate to determine the number of square miles in which you would find 486 deer.
Answer:
\(\frac{486}{9}\) = 54
In 54 square miles, you would find 486 deer.
→ Based upon the discussion of the questions above, answer the question: Do conservationists need to be worried? Be sure to support your answer with mathematical reasoning about rate and unit rate.
You Need WHAT?
While working on Example 2, encourage students to make a chart to organize the data from the problem.
Example 2.
Brandon came home from school and informed his mother that he had volunteered to make cookies for his entire grade level. He needs 3 cookies for each of the 96 students in seventh grade. Unfortunately, he needs the cookies the very next day! Brandon and his mother determined that they can fit 36 cookies on two cookie sheets.
a. Is the number of cookies proportional to the number of cookie sheets used in baking? Create a table that shows data for the number of sheets needed for the total number of cookies baked.
Table:
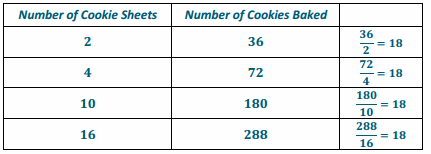
The unit rate of \(\frac{y}{x}\) is __.
Answer:
Constant of Proportionality:
Answer:
k = 18
Explain the meaning of the constant of proportionality in this problem:
Answer:
There are 18 cookies per 1 cookie sheet.
b. It takes 2 hours to bake 8 sheets of cookies. If Brandon and his mother begin baking at 4:00 p.m., when will they finish baking the cookies?
Answer:
96 students (3 cookies per student) =288 cookies
\(\frac{288 \text { cookies }}{18 \text { cookies per sheet }}\) = 16 sheets of cookies
If it takes 2 hours to bake 8 sheets, it will take 4 hours to bake 16 sheets of cookies. They will finish baking at 8:00 p.m
Example 3.
French Class cooking
Suzette and Margo want to prepare crêpes for all of the students in their French class. A recipe makes 20 crêpes with a certain amount of flour, milk, and 2 eggs. The girls already know that they have plenty of flour and milk to make 50 crêpes, but they need to determine the number of eggs they will need for the recipe because they are not sure they have enough.
a. Considering the amount of eggs necessary to make the crêpes, what is the constant of proportionality?
Answer:
![]()
The constant of proportionality is \(\frac{1}{10}\).
b. What does the constant or proportionality mean in the context of this problem?
Answer:
One egg is needed to make 10 crepes.
c. How many eggs are needed to make 50 crepes?
Answer:
50(\(\frac{1}{10}\)) = 5
Five eggs are needed to make 50 crepes.
Eureka Math Grade 7 Module 1 Lesson 7 Problem Set Answer Key
For each of the following problems, define the constant of proportionality to answer the follow-up question.
Question 1.
Bananas are $0.59/pound.
a. What is the constant of proportionality, or k?
Answer:
The constant of proportionality, k, is 0.59.
b. How much will 25 pounds of bananas cost?
Answer:
25 lb.($0.59/lb.)=$14.75
Question 2.
The dry cleaning fee for 3 pairs of pants is $18.
a. What is the constant of proportionality?
Answer:
\(\frac{18}{3}\) = 6, so k is 6.
b. How much will the dry cleaner charge for 11 pairs of pants?
Answer:
6(11) = 66
The dry cleaner would charge $66.
Question 3.
For every $5 that Micah saves, his parents give him $10.
a. What is the constant of proportionality?
Answer:
\(\frac{10}{5}\) = 2, so k is 2.
b. If Micah saves $150, how much money will his parents give him?
Answer:
2($150)=$300
Question 4.
Each school year, the seventh graders who study Life Science participate in a special field trip to the city zoo. In 2010, the school paid $1,260 for 84 students to enter the zoo. In 2011, the school paid $1,050 for 70 students to enter the zoo. In 2012, the school paid $1,395 for 93 students to enter the zoo.
a. Is the price the school pays each year in entrance fees proportional to the number of students entering the zoo?
Answer:
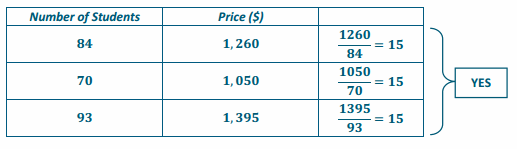
b. Explain why or why not.
Answer:
The price is proportional to the number of students because the ratio of the entrance fee paid per student was the same.
\(\frac{1260}{84}\) = 15
c. Identify the constant of proportionality and explain what it means in the context of this situation.
Answer:
The constant of proportionality (k) is 15. This represents the price per student.
d. What would the school pay if 120 students entered the zoo?
Answer:
120 “students” ($15″ per student” )=$1800
e. How many students would enter the zoo if the school paid $1,425?
Answer:
\(\frac{1425}{15}\) = 95 students
Eureka Math Grade 7 Module 1 Lesson 7 Exit Ticket Answer Key
Susan and John are buying cold drinks for a neighborhood picnic. Each person is expected to drink one can of soda. Susan says that if you multiply the unit price for a can of soda by the number of people attending the picnic, you will be able to determine the total cost of the soda. John says that if you divide the cost of a 12-pack of soda by the number of sodas, you will determine the total cost of the sodas. Who is right, and why?
Answer:
Susan is correct. The table below shows that if you multiply the unit price, say 0.50, by the number of people, say 12, you will determine the total cost of the soda. I created a table to model the proportional relationship. I used a unit price of 0.50 to make the comparison.
Susan
| Number of People | 2 | 3 | 4 | 12 |
| Total Cost of Soda (in dollars) | 1 | 1.50 | 2 | 6 |
I used the same values to compare to John. \(\frac{\text { total cost }}{12 \text { people }}\)= ?
The total cost is $6, and there 12 people. \(\frac{6}{12}\) = \(\frac{1}{2}\), which is $0.50 or the unit price, not the total cost.