Engage NY Eureka Math 7th Grade Module 2 Mid Module Assessment Answer Key
Eureka Math Grade 7 Module 2 Mid Module Assessment Task Answer Key
Question 1.
Diamond used a number line to add. She started counting at 10, and then she counted until she was on the number -4 on the number line.
a. If Diamond is modeling addition, what number did she add to 10? Use the number line below to model your answer.

Answer:

10 + -14 = -4
Diamond added -14 to 10.
b. Write a real-world story problem that would fit this situation.
Answer:
Diamond had $10 and put it in the bank. She forgot about the monthly bank fee of $14.
Now her account has a balance of -$4.
c. Use absolute value to express the distance between 10 and -4.
Answer:
|10 – (-4)|
|10 + 4|
|14|
14
The distance between 10 and -4 is 14.
Question 2.
What value of a will make the equation a true statement? Explain how you arrived at your solution.
(-\(\frac{3}{4}\) + \(\frac{4}{3}\))
Answer:
(-\(\frac{3}{4}\) + \(\frac{4}{3}\))+a=0
(-\(\frac{3}{4}\) + \(\frac{4}{3}\) )
(-\(\frac{9}{12}\) + \(\frac{16}{12}\))
\(\frac{7}{12}\) + a = 0
a = –\(\frac{7}{12}\)
The value of a has to be –\(\frac{7}{12}\) because that’s the additive inverse of \(\frac{7}{12}\).
Question 3.
Every month, Ms. Thomas pays her car loan through automatic payments (withdrawals) from her savings account. She pays the same amount on her car loan each month. At the end of the year, her savings account balance changed by -$2,931 from payments made on her car loan.
a. What is the change in Ms. Thomas’ savings account balance each month due to her car payment?
Answer:
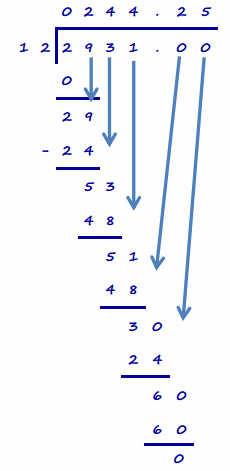
Her monthly payment is $244.25, so her account balance changes each month by -$244.25 when her payment is made.
b. Describe the total change to Ms. Thomas’ savings account balance after making six monthly payments on her car loan. Model your answer using a number sentence.
Answer:
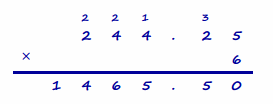
6 × (-244.25) = -1,465.50
Ms. Thomas’ car loan changed her savings account balance by -$1,465.50 after “6” monthly payments.
Question 4.
Jesse and Miya are playing the Integer Card Game. The cards in Jesse’s hand are shown below:
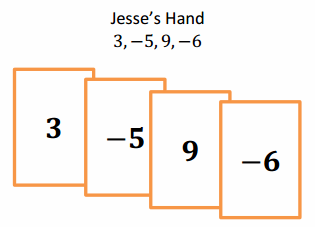
a. What is the total score of Jesse’s hand? Support your answer by showing your work.
Answer:
3 + (-5 ) + 9 + (- 6)
(-2) + 3
1
Jesse’s score is 1.
b. Jesse picks up two more cards, but they do not affect his overall point total. State the value of each of the two cards, and tell why they do not affect his overall point total.
Answer:
3 + (-5) + 9 + (-6)
(-2) + 3
1
Jesse’s score is 1.
b. Jesse picks up two more cards, but they do not affect his overall point total. State the value of each of the two cards, and tell why they do not affect his overall point total.
Answer:
The values of the two cards must be opposites, such as -2 and 2, because opposites combine to get 0. 0 will not change the score in his hand.
c. Complete Jesse’s new hand to make this total score equal zero. What must be the value of the ? card? Explain how you arrived at your answer.
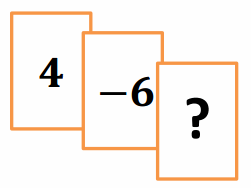
Answer:
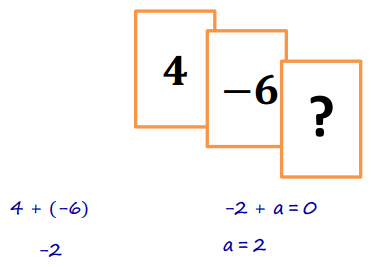
The two given cards total -2. To get a sum of zero, I have to combine -2 with its opposite 2 because additive inverses (opposites) combine to get 0.
Question 5.
Michael’s father bought him a 16-foot board to cut into shelves for his bedroom. Michael plans to cut the board into 11 equal size lengths for his shelves.
a. The saw blade that Michael will use to cut the board will change the length of the board by -0.125 inches for each cut. How will this affect the total length of the board?
Answer:

The board will be cut in 10 places.

The 10 cuts take away 1.25 inches of the total length of the board. The usable length of the board is 1.25 inches shorter than 16 feet.
b. After making his cuts, what will the exact length of each shelf be?
Answer:
The board begins at 192 inches long.
192 – 1.25 = 190.75. The length of the board that can be used with the blade widths removed is 190.75 inches.
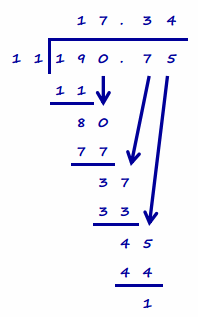
Continue the long division, and there will be a repeating remainder of 1. Therefore, the lengths of the shelves should be exactly \(17.34 \overline{09}\) inches.
Question 6.
Bryan and Jeanette were playing the Integer Card Game like the one you played in class. They were practicing adding and subtracting integers. Jeanette had a score of -10. Bryan took away one of Jeanette’s cards. He showed it to her. It was a -8. Jeanette recalculated her score to be -2, but Bryan disagreed. He said that her score should be -18 instead. Read their conversation and answer the question below.
“No Jeanette, removing a negative card means the same thing as subtracting a positive. So, negative 10 minus negative 8 is negative 18.”
“It does not! Removing a negative card is the same as adding the same positive card. My score will go up. Negative 10 minus negative 8 is negative 2.”
Based on their disagreement, who, if anyone, is right? Explain.
Answer:
Jeanette is correct that removing a negative is the same as adding the same positive card. Having a negative card in your hand decreases your score. If you remove that negative card, your score is no longer decreased by the card, so your score goes up.
Question 7.
The table below shows the temperature changes Monday morning in Bedford, New York over a 4-hour period after a cold front came through.
a. If the beginning temperature was -13°F at 5:00 a.m., what was the temperature at 9:00 a.m.?
Change in Temperature
Answer:
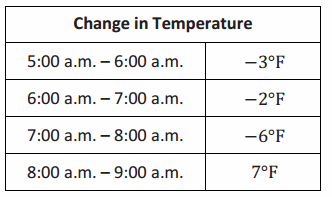
-13 + (-3) + (-2) + (-6) + 7
(-16) + (-8) + 7
-24 + 7
-17°F
The temperature at 9:00 a.m. was -17°F.
b. The same cold front hit Hartford, Connecticut the next morning. The temperature dropped by 7° each hour from 5:00 a.m. to 9:00 a.m. What was the beginning temperature at 5:00 a.m. if the temperature at 9:00 a.m. was -10°F?
Answer:
-10 + 4(7)
-10 + 28
18° F
The beginning temperature at 5:00 a.m. was 18°F.
c. In answering part (b), Josiah and Kate used different methods. Josiah said his method involved multiplication, while Kate said she did not use multiplication. Both students arrived at the correct answer. How is this possible? Explain.
Answer:
The temperature change was the same for each hour, so Josiah multiplied the 7-degree drop by 4 hours. Kate added the 7-degree drop 4 times. Kate used repeated addition, which is the same as multiplication.