Engage NY Eureka Math 7th Grade Module 3 Lesson 17 Answer Key
Eureka Math Grade 7 Module 3 Lesson 17 Exploratory Challenge Answer Key
Exploratory Challenge
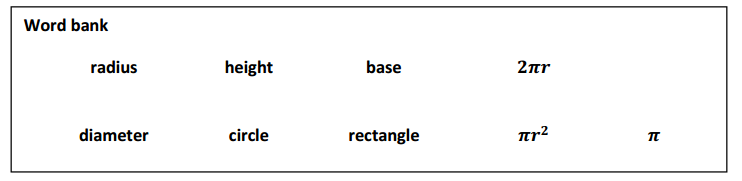
To find the formula for the area of a circle, cut a circle into 16 equal pieces.
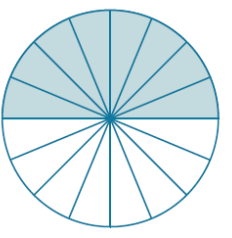
Arrange the triangular wedges by alternating the “triangle” directions and sliding them together to make a “parallelogram.” Cut the triangle on the left side in half on the given line, and slide the outside half of the triangle to the other end of the parallelogram in order to create an approximate “rectangle.”
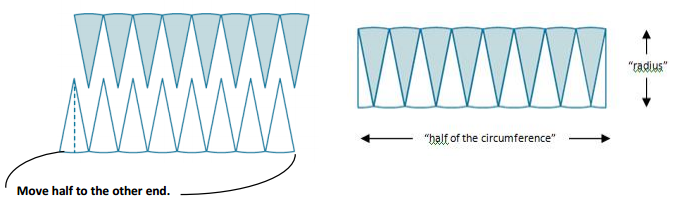
The circumference is 2πr, where the radius is r. Therefore, half of the circumference is πr.
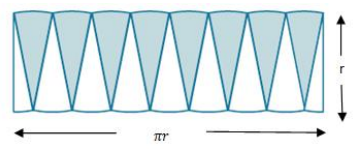
What is the area of the “rectangle” using the side lengths above?
Answer:
The area of the “rectangle” is base times height, and, in this case, A = πr ∙ r.
Are the areas of the “rectangle” and the circle the same?
Answer:
Yes, since we just rearranged pieces of the circle to make the “rectangle,” the area of the “rectangle” and the area of the circle are approximately equal. Note that the more sections we cut the circle into, the closer the approximation.
If the area of the rectangular shape and the circle are the same, what is the area of the circle?
Answer:
The area of a circle is written as A = πr ∙ r, or A = πr2.
Eureka Math Grade 7 Module 3 Lesson 17 Example Answer Key
Example 1.
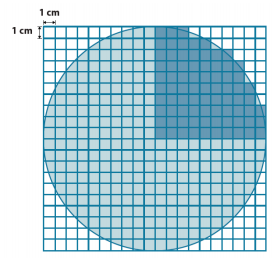
Use the shaded square centimeter units to approximate the area of the circle.
Question 1.
What is the radius of the circle?
Answer:
10 cm
Question 2.
What would be a quicker method for determining the area of the circle other than counting all of the squares in the entire circle?
Answer:
Count \(\frac{1}{4}\) of the squares needed; then, multiply that by four in order to determine the area of the entire circle.
Question 3.
Using the diagram, how many squares were used to cover one-fourth of the circle?
Answer:
The area of one-fourth of the circle is approximately 79 cm2.
Question 4.
What is the area of the entire circle?
Answer:
A ≈ 4 ∙ 79 cm2
A ≈ 316 cm2
Example 2.
A sprinkler rotates in a circular pattern and sprays water over a distance of 12 feet. What is the area of the circular region covered by the sprinkler? Express your answer to the nearest square foot.
Draw a diagram to assist you in solving the problem. What does the distance of 12 feet represent in this problem?
Answer:
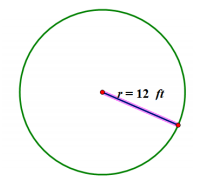
The radius is 12 feet.
What information is needed to solve the problem?
Answer:
The formula to find the area of a circle is A = πr2. If the radius is 12 ft., then A = π ∙ (12 ft.)2 = 144π ft2, or approximately 452 ft2.
Example 3.
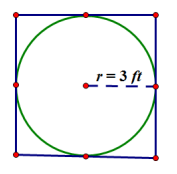
Suzanne is making a circular table out of a square piece of wood. The radius of the circle that she is cutting is 3 feet. How much waste will she have for this project? Express your answer to the nearest square foot.
Draw a diagram to assist you in solving the problem. What does the distance of 3 feet represent in this problem?
Answer:
The radius of the circle is 3 feet.
Question 1.
What information is needed to solve the problem?
Answer:
The area of the circle and the area of the square are needed so that we can subtract the area of the circle from the area of the square to determine the amount of waste.
Question 2.
What information do we need to determine the area of the square and the circle?
Answer:
Circle: just radius because A = πr2 Square: one side length
Question 3.
How will we determine the waste?
Answer:
The waste is the area left over from the square after cutting out the circular region. The area of the circle is
A = π ∙ (3 ft.)2 = 9π ft2 ≈ 28.26 ft2. The area of the square is found by first finding the diameter of the circle, which is the same as the side of the square. The diameter is d = 2r; so, d = 2 ∙ 3 ft. or 6 ft. The area of a square is found by multiplying the length and width, so A = 6 ft. ∙ 6 ft. = 36 ft2. The solution is the difference between the area of the square and the area of the circle, so 36 ft2-28.26 ft2 ≈ 7.74 ft2.
Question 4.
Does your solution answer the problem as stated?
Answer:
Yes, the amount of waste is 7.74 ft2.
Eureka Math Grade 7 Module 3 Lesson 17 Exercise Answer Key
Exercises 1–3
Solve the problem below individually. Explain your solution.
Exercise 1.
Find the radius of a circle if its circumference is 37.68 inches. Use π ≈ 3.14.
Answer:
If C = 2πr, then 37.68 = 2πr. Solving the equation for r,
37.68 = 2πr
(\(\frac{1}{2 \pi}\))37.68 = (\(\frac{1}{2 \pi}\))2πr
\(\frac{1}{6.28}\) (37.68) ≈ r
6 ≈ r
The radius of the circle is approximately 6 in.
Exercise 2.
Determine the area of the rectangle below. Name two ways that can be used to find the area of the rectangle.
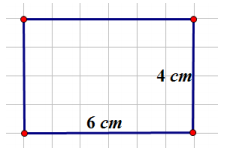
Answer:
The area of the rectangle is 24 cm2. The area can be found by counting the square units inside the rectangle or by multiplying the length (6 cm) by the width (4 cm).
Exercise 3.
Find the length of a rectangle if the area is 27 cm2 and the width is 3 cm.
Answer:
If the area of the rectangle is Area = length ∙ width, then
27 cm2 = l ∙ 3 cm
\(\frac{1}{3}\) ∙ 27 cm2 = \(\frac{1}{3}\) ∙ l ∙ 3 cm
9 cm = l
Exercises 4–6
Exercise 4.
A circle has a radius of 2 cm.
a. Find the exact area of the circular region.
Answer:
A = π ∙ (2 cm)2 = 4π cm2
b. Find the approximate area using 3.14 to approximate π.
Answer:
A = 4 cm2 ∙ π ≈ 4 cm2 ∙ 3.14 ≈ 12.56 cm2
Exercise 5.
A circle has a radius of 7 cm.
a. Find the exact area of the circular region.
Answer:
A = π ∙ (7 cm)2 = 49π cm2
b. Find the approximate area using \(\frac{22}{7}\) to approximate π.
Answer:
A = 49 ∙ π cm2 ≈ (49 ∙ \(\frac{22}{7}\) ) cm2 ≈ 154 cm2
c. What is the circumference of the circle?
Answer:
C = 2π ∙ 7 cm = 14π cm ≈ 43.96 cm
Exercise 6.
Joan determined that the area of the circle below is 400π cm2. Melinda says that Joan’s solution is incorrect; she believes that the area is 100π cm2. Who is correct and why?
Answer:
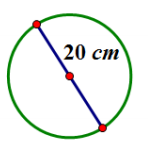
Melinda is correct. Joan found the area by multiplying π by the square of 20 cm (which is the diameter) to get a result of 400π cm2, which is incorrect. Melinda found that the radius was 10 cm (half of the diameter). Melinda multiplied π by the square of the radius to get a result of 100π cm2.
Eureka Math Grade 7 Module 3 Lesson 17 Problem Set Answer Key
Question 1.
The following circles are not drawn to scale. Find the area of each circle. (Use \(\frac{22}{7}\) as an approximation for π.)
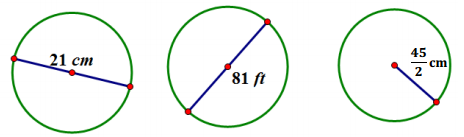
Answer:
Question 2.
A circle has a diameter of 20 inches.
a. Find the exact area, and find an approximate area using π ≈ 3.14.
Answer:
If the diameter is 20 in., then the radius is 10 in. If A = πr2, then A = π ∙ (10 in.)2 or 100π in2.
A ≈ (100 ∙ 3.14) in2 ≈ 314 in2.
b. What is the circumference of the circle using π ≈ 3.14 ?
Answer:
If the diameter is 20 in., then the circumference is C = πd or C ≈ 3.14 ∙ 20 in. ≈ 62.8 in.
Question 3.
A circle has a diameter of 11 inches.
a. Find the exact area and an approximate area using π ≈ 3.14.
Answer:
If the diameter is 11 in., then the radius is \(\frac{11}{2}\) in. If A = πr2, then A = π ∙ (\(\frac{11}{2}\) in.)2or \(\frac{121}{4}\) π in2.
A ≈ (\(\frac{121}{4}\) ∙ 3.14) in2 ≈ 94.985 in2
b. What is the circumference of the circle using π ≈ 3.14?
Answer:
If the diameter is 11 inches, then the circumference is C = πd or C ≈ 3.14 ∙ 11 in. ≈ 34.54 in.
Question 4.
Using the figure below, find the area of the circle.
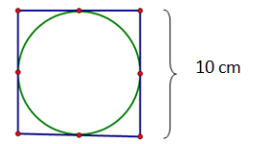
Answer:
In this circle, the diameter is the same as the length of the side of the square. The diameter is 10 cm; so, the radius is 5 cm. A = πr2, so A = π(5 cm)2 = 25π cm2.
Question 5.
A path bounds a circular lawn at a park. If the inner edge of the path is 132 ft. around, approximate the amount of area of the lawn inside the circular path. Use π ≈ \(\frac{22}{7}\) .
Answer:
The length of the path is the same as the circumference. Find the radius from the circumference; then, find the area.
C = 2πr
132 ft. ≈ 2 ∙ \(\frac{22}{7}\) ∙ r
132 ft. ≈ \(\frac{44}{7}\) r
\(\frac{7}{44}\) ∙ 132 ft. ≈ \(\frac{7}{44}\) ∙ \(\frac{44}{7}\) r
21 ft. ≈ r
A ≈ \(\frac{22}{7}\) ∙ (21 ft.)2
A ≈ 1386 ft2
Question 6.
The area of a circle is 36π cm2. Find its circumference.
Answer:
Find the radius from the area of the circle; then, use it to find the circumference.
A = πr2
36π cm2 = πr2
\(\frac{1}{\pi}\) ∙ 36π cm2 = \(\frac{1}{\pi}\) ∙ πr2
36 cm2 = r2
6 cm = r
C = 2πr
C = 2π ∙ 6 cm
C = 12π cm
Question 7.
Find the ratio of the area of two circles with radii 3 cm and 4 cm.
Answer:
The area of the circle with radius 3 cm is 9π cm2. The area of the circle with the radius 4 cm is 16π cm2. The ratio of the area of the two circles is 9π:16π or 9:16.
Question 8.
If one circle has a diameter of 10 cm and a second circle has a diameter of 20 cm, what is the ratio of the area of the larger circle to the area of the smaller circle?
Answer:
The area of the circle with the diameter of 10 cm has a radius of 5 cm. The area of the circle with the diameter of 10 cm is π ∙ (5 cm)2, or 25π cm2. The area of the circle with the diameter of 20 cm has a radius of 10 cm. The area of the circle with the diameter of 20 cm is π ∙ (10 cm)2 or 100π cm2. The ratio of the diameters is 20 to 10 or 2:1, while the ratio of the areas is 100π to 25π or 4:1.
Question 9.
Describe a rectangle whose perimeter is 132 ft. and whose area is less than 1 ft2. Is it possible to find a circle whose circumference is 132 ft. and whose area is less than 1 ft2? If not, provide an example or write a sentence explaining why no such circle exists.
Answer:
A rectangle that has a perimeter of 132 ft. can have a length of 65.995 ft. and a width of 0 .005 ft. The area of such a rectangle is 0.329975 ft2, which is less than 1 ft2. No, because a circle that has a circumference of 132 ft. has a radius of approximately 21 ft.
A = πr2 = π(21)2 = 1387.96 ≠ 1
Question 10.
If the diameter of a circle is double the diameter of a second circle, what is the ratio of the area of the first circle to the area of the second?
Answer:
If I choose a diameter of 24 cm for the first circle, then the diameter of the second circle is 12 cm. The first circle has a radius of 12 cm and an area of 144π cm2. The second circle has a radius of 6 cm and an area of 36π cm2. The ratio of the area of the first circle to the second is 144π to 36π , which is a 4 to 1 ratio. The ratio of the diameters is 2, while the ratio of the areas is the square of 2, or 4.
Eureka Math Grade 7 Module 3 Lesson 17 Exit Ticket Answer Key
Complete each statement using the words or algebraic expressions listed in the word bank below.
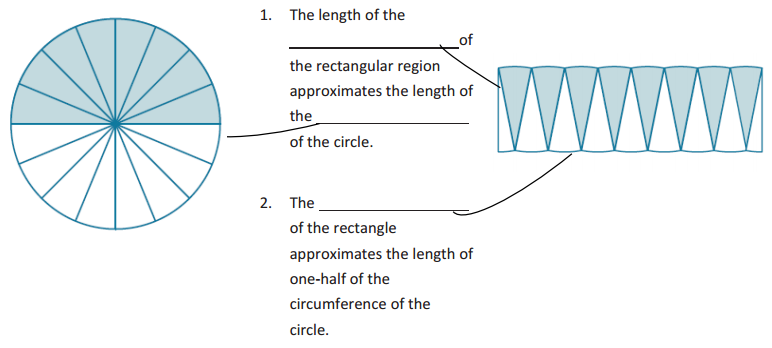
Answer:
1. The length of the height of the rectangular region approximates the length of the radius of the circle.
2. The base of the rectangle approximates the length of one-half of the circumference of the circle.
Question 3.
The circumference of the circle is _______________________.
Answer:
The circumference of the circle is 2πr.
Question 4.
The _________________ of the ___________________ is 2r.
Answer:
The diameter of the circle is 2r.
Question 5.
The ratio of the circumference to the diameter is ______.
Answer:
The ratio of the circumference to the diameter is π.
Question 6.
Area (circle) = Area of (_____________) = \(\frac{1}{2}\) ∙ circumference ∙ r = \(\frac{1}{2}\) (2πr) ∙ r = π ∙ r ∙ r = _____________.
Answer:
Area (circle) = Area of (rectangle) = \(\frac{1}{2}\) ∙ circumference ∙ r = \(\frac{1}{2}\) (2πr) ∙ r = π ∙ r ∙ r = πr2.