Engage NY Eureka Math 7th Grade Module 3 Lesson 5 Answer Key
Eureka Math Grade 7 Module 3 Lesson 5 Example Answer Key
Example 1.
Write the sum, and then write an equivalent expression by collecting like terms and removing parentheses.
a. 2x and – 2x + 3
Answer:
2x + (- 2x + 3)
(2x + (- 2x)) + 3 Associative property, collect like terms
0 + 3 Additive inverse
3 Additive identity property of zero
b. 2x – 7 and the opposite of 2x
Answer:
2x + (- 7) + (- 2x)
2x + (- 2x) + (- 7) Commutative property, associative property
0 + (- 7) Additive inverse
– 7 Additive identity property of zero
c. The opposite of (5x – 1) and 5x
Answer:
– (5x – 1) + 5x
– 1(5x – 1) + 5x Taking the opposite is equivalent to multiplying by –1.
– 5x + 1 + 5x Distributive property
(- 5x + 5x) + 1 Commutative property, any order property
0 + 1 Additive inverse
1 Additive identity property of zero
Example 2.
• (\(\frac{3}{4}\))×(\(\frac{4}{3}\) )=
Answer:
1
• 4×\(\frac{1}{4}\) =
Answer:
1
• \(\frac{1}{9}\) ×9=
Answer:
1
• (- \(\frac{1}{3}\) )× – 3=
Answer:
1
• (- \(\frac{6}{5}\) )×(- 5/6)=
Answer:
1
→ What are these pairs of numbers called?
→ Reciprocals
→ What is another term for reciprocal?
→ The multiplicative inverse
→ What happens to the sign of the expression when converting it to its multiplicative inverse?
→ There is no change to the sign For example, the multiplicative inverse of – 2 is (- \(\frac{1}{2}\) ) The negative sign remains the same.
→ What can you conclude from the pattern in the answers?
→ The product of a number and its multiplicative inverse is equal to 1.
→ Earlier, we saw that 0 is a special number because it is the only number that when added to another number, results in that number again Can you explain why the number 1 is also special?
→ One is the only number that when multiplied with another number, results in that number again.
→ This property makes 1 special among all the numbers Mathematicians have a special name for 1, the multiplicative identity; they call the property the multiplicative identity property of one.
As an extension, ask students if there are any other special numbers that they have learned Students should respond: Yes; – 1 has the property that multiplying a number by it is the same as taking the opposite of the number Share with students that they are going to learn later in this module about another special number called pi.
As a class, write the product, and then write an equivalent expression in standard form State the properties for each step After discussing questions, review the properties and definitions in the Lesson Summary emphasizing the multiplicative identity property of one and the multiplicative inverse.
Write the product, and then write the expression in standard form by removing parentheses and combining like terms Justify each step.
a. The multiplicative inverse of \(\frac{1}{5}\) and (2x – \(\frac{1}{5}\) )
Answer:
5(2x – \(\frac{1}{5}\) )
5(2x) – 5\(\frac{1}{5}\) Distributive property
10x – 1 Multiplicative inverses
b. The multiplicative inverse of 2 and (2x + 4)
Answer:
(\(\frac{1}{2}\) )(2x + 4)
(\(\frac{1}{2}\) )(2x) + (\(\frac{1}{2}\) )(4) Distributive property
1x + 2 Multiplicative inverses, multiplication
x + 2 Multiplicative identity property of one
c. The multiplicative inverse of (\(\frac{1}{3x + 5}\) ) and \(\frac{1}{3}\)
Answer:
(3x + 5)∙\(\frac{1}{3}\)
3x(\(\frac{1}{3}\) ) + 5(\(\frac{1}{3}\) ) Distributive property
1x + \(\frac{5}{3}\) Multiplicative inverse
x + \(\frac{5}{3}\) Multiplicative identity property of one
Eureka Math Grade 7 Module 3 Lesson 5 Opening Exercise Answer Key
a. In the morning, Harrison checked the temperature outside to find that it was – 12°F Later in the afternoon, the temperature rose 12°F Write an expression representing the temperature change What was the afternoon temperature?
Answer:
– 12 + 12; the afternoon temperature was 0°F.
b. Rewrite subtraction as adding the inverse for the following problems and find the sum.
i. 2 – 2
Answer:
2 + (- 2)=0
ii – 4 – (- 4)
Answer:
(- 4) + 4=0
iii. The difference of 5 and 5
Answer:
5 – 5=5 + (- 5)=0
iv. g – g
g + (- g)=0
c. What pattern do you notice in part (a) and (b)?
Answer:
The sum of a number and its additive inverse is equal to zero.
d. Add or subtract.
i. 16 + 0
Answer:
16
ii. 0 – 7
Answer:
0 + (- 7)= – 7
iii – 4 + 0
– 4
iv. 0 + d
Answer:
d
v. What pattern do you notice in parts (i) through (iv)?
Answer:
The sum of any quantity and zero is equal to the value of the quantity.
e. Your younger sibling runs up to you and excitedly exclaims, “I’m thinking of a number If I add it to the number 2 ten times, that is, 2 + my number + my number + my number, and so on, then the answer is 2 What is my number?” You almost immediately answer, “zero,” but are you sure? Can you find a different number (other than zero) that has the same property? If not, can you justify that your answer is the only correct answer?
Answer:
No, there is no other number On a number line, 2 can be represented as a directed line segment that starts at 0, ends at 2, and has length 2 Adding any other (positive or negative) number v to 2 is equivalent to attaching another directed line segment with length |v| to the end of the first line segment for 2:
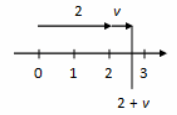
If v is any number other than 0, then the directed line segment that represents v will have to have some length, so 2 + v will have to be a different number on the number line Adding v again just takes the new sum further away from the point 2 on the number line.
Eureka Math Grade 7 Module 3 Lesson 5 Exercise Answer Key
Exercise 1
With a partner, take turns alternating roles as writer and speaker The speaker verbalizes how to rewrite the sum and properties that justify each step as the writer writes what is being spoken without any input At the end of each problem, discuss in pairs the resulting equivalent expressions.
Write the sum, and then write an equivalent expression by collecting like terms and removing parentheses whenever possible.
a – 4 and 4b + 4
Answer:
– 4 + (4b + 4)
(- 4 + 4) + 4b Any order, any grouping
0 + 4b Additive inverse
4b Additive identity property of zero
b. 3x and 1 – 3x
Answer:
3x + (1 – 3x)
3x + (1 + (- 3x)) Subtraction as adding the inverse
(3x + (- 3x)) + 1 Any order, any grouping
0 + 1 Additive inverse
1 Additive identity property of zero
c. The opposite of 4x and – 5 + 4x
Answer:
– 4x + (- 5 + 4x)
(- 4x + 4x) + (- 5) Any order, any grouping
0 + (- 5) Additive inverse
– 5 Additive identity property of zero
d. The opposite of – 10t and t – 10t
Answer:
10t + (t – 10t)
(10t + (- 10t)) + t Any order, any grouping
0 + t Additive inverse
t Additive identity property of zero
e. The opposite of (- 7 – 4v) and – 4v
Answer:
– (- 7 – 4v) + (- 4v)
– 1(- 7 – 4v) + (- 4v) Taking the opposite is equivalent to multiplying by –1.
7 + 4v + (- 4v) Distributive property
7 + 0 Any grouping, additive inverse
7 Additive identity property of zero
Exercise 2.
Write the product, and then write the expression in standard form by removing parentheses and combining like terms Justify each step.
a. The reciprocal of 3 and – 6y – 3x
Answer:
(\(\frac{1}{3}\) )(- 6y + (- 3x)) Rewrite subtraction as an addition problem
(\(\frac{1}{3}\) )(- 6y) + (\(\frac{1}{3}\) )(- 3x) Distributive property
– 2y – 1x Multiplicative inverse
– 2y – x Multiplicative identity property of one
b. The multiplicative inverse of 4 and 4h – 20
Answer:
(\(\frac{1}{4}\) )(4h + (- 20)) Rewrite subtraction as an addition problem
(\(\frac{1}{4}\) )(4h) + (\(\frac{1}{4}\) )(- 20) Distributive property
1h + (- 5) Multiplicative inverse
h – 5 Multiplicative identity property of one
c. The multiplicative inverse of – \(\frac{1}{6}\) and 2 – \(\frac{1}{6}\) j
(- 6)(2 + (- \(\frac{1}{6}\) j)) Rewrite subtraction as an addition problem
(- 6)(2) + (- 6)(- \(\frac{1}{6}\) j) Distributive property
– 12 + 1j Multiplicative inverse
– 12 + j Multiplicative identity property of one
Eureka Math Grade 7 Module 3 Lesson 5 Problem Set Answer Key
Question 1.
Fill in the missing parts.
a. The sum of 6c – 5 and the opposite of 6c
(6c – 5) + (- 6c)
_____ Rewrite subtraction as addition
Answer:
(6c + (- 5)) + (- 6c)
6c + (- 6c) + (- 5)
Regrouping/any order (or commutative property of addition)
0 + (- 5) ___
Answer:
Additive inverse
__ Additive identity property of zero
Answer:
– 5
b. The product of – 2c + 14 and the multiplicative inverse of – 2
(- 2c + 14)(- \(\frac{1}{2}\) )
(- 2c)(- \(\frac{1}{2}\) ) + (14)(- \(\frac{1}{2}\) )
Distributive property
__ Multiplicative inverse, multiplication
1c + (- 7)
1c – 7 Adding the additive inverse is the same as subtraction
c – 7 ____
Answer:
Multiplicative identity property of one
Question 2.
Write the sum, and then rewrite the expression in standard form by removing parentheses and collecting like terms.
a. 6 and p – 6
Answer:
6 + (p – 6)
6 + (- 6) + p
0 + p
p
b. 10w + 3 and – 3
Answer:
(10w + 3) + (- 3)
10w + (3 + (- 3))
10w + 0
10w
c – x – 11 and the opposite of – 11
Answer:
(- x + (- 11)) + 11
– x + ((- 11) + (11))
– x + 0
– x
d. The opposite of 4x and 3 + 4x
Answer:
(- 4x) + (3 + 4x)
((- 4x) + 4x) + 3
0 + 3
3
e. 2g and the opposite of (1 – 2g)
Answer:
2g + (- (1 – 2g))
2g + (- 1) + 2g
2g + 2g + (- 1)
4g + (- 1)
4g – 1
Question 3.
Write the product, and then rewrite the expression in standard form by removing parentheses and collecting like terms.
a. 7h – 1 and the multiplicative inverse of 7
Answer:
(7h + (- 1))(\(\frac{1}{7}\) )
(\(\frac{1}{7}\) )(7h) + (\(\frac{1}{7}\) )(- 1)
h – \(\frac{1}{7}\)
b. The multiplicative inverse of – 5 and 10v – 5
(- \(\frac{1}{5}\) )(10v – 5)
(- \(\frac{1}{5}\) )(10v) + (- \(\frac{1}{5}\) )(- 5)
– 2v + 1
Eureka Math Grade 7 Module 3 Lesson 5 Exit Ticket Answer Key
Question 1.
Find the sum of 5x + 20 and the opposite of 20 Write an equivalent expression in standard form Justify each step.
Answer:
(5x + 20) + (- 20)
5x + (20 + (- 20)) Associative property of addition
5x + 0 Additive inverse
5x Additive identity property of zero
Question 2.
For 5x + 20 and the multiplicative inverse of 5, write the product and then write the expression in standard form, if possible Justify each step.
Answer:
(5x + 20)(\(\frac{1}{5}\) )
(5x)(\(\frac{1}{5}\) ) + 20(\(\frac{1}{5}\) ) Distributive property
1x + 4 Multiplicative inverses, multiplication
x + 4 Multiplicative identity property of one