Engage NY Eureka Math 7th Grade Module 4 Lesson 2 Answer Key
Eureka Math Grade 7 Module 4 Lesson 2 Example Answer Key
Example 2: A Numeric Approach to Finding a Part, Given a Percent of the Whole
In Ty’s English class, 70% of the students completed an essay by the due date. There are 30 students in Ty’s English class. How many completed the essay by the due date?
Answer:
Whole → 100%
30 → 100%
\(\frac{30}{100}\) → 1%
70 ∙ \(\frac{3}{100}\) → 21
21 → 70%
70% of 30 is 21, so 21 of the students in Ty’s English class completed their essays on time.
Example 3: An Algebraic Approach to Finding a Part, Given a Percent of the Whole
A bag of candy contains 300 pieces of which 28% are red. How many pieces are red?
Which quantity represents the whole?
Answer:
The total number of candies in the bag, 300, is the whole because the number of red candies is being compared to it.
Which of the terms in the percent equation is unknown? Define a letter (variable) to represent the unknown quantity.
Answer:
We do not know the part, which is the number of red candies in the bag. Let r represent the number of red candies in the bag.
Write an expression using the percent and the whole to represent the number of pieces of red candy.
Answer:
\(\frac{28}{100}\) ∙ (300), or 0.28∙(300), is the amount of red candy since the number of red candies is 28% of the 300 pieces of candy in the bag.
Write and solve an equation to find the unknown quantity.
Part = Percent × Whole
r = \(\frac{28}{100}\) ∙ (300)
r 28 ∙ 3
r = 84
There are 84 red pieces of candy in the bag.
Example 4: Comparing Part of a Whole to the Whole with the Percent Formula
Zoey inflated 24 balloons for decorations at the middle school dance. If Zoey inflated 15% of the total number of balloons inflated for the dance, how many balloons are there total? Solve the problem using the percent formula, and verify your answer using a visual model.
Answer:
Part = Percent×Whole
The part is 24 balloons, and the percent is 15%, so let t represent the unknown total number of balloons.
24 = \(\frac{15}{100}\) t If a = b, then ac = bc.
\(\frac{100}{15}\) (24) = \(\frac{100}{15}\) (\(\frac{15}{100}\))t Multiplicative inverse
\(\frac{2400}{15}\) = 1t Multiplicative identity property of 1 and equivalent fractions
160 = t
The total number of balloons to be inflated for the dance was 160 balloons.
15% → 24
1% → \(\frac{24}{15}\) We want the quantity that corresponds with 100%, so first we find 1%.*
100% → \(\frac{24}{15}\) ∙ 100
100% → \(\frac{24}{3}\) ∙ 20
100% → 160
Student may also find 5% as is shown in the tape diagram below.
The total number of balloons to be inflated for the dance was 160 balloons.

Example 5: Finding the Percent Given a Part of the Whole and the Whole
Haley is making admission tickets to the middle school dance. So far she has made 112 tickets, and her plan is to make 320 tickets. What percent of the admission tickets has Haley produced so far? Solve the problem using the percent formula, and verify your answer using a visual model.
Answer:
Part = Percent×Whole
The part is 112 tickets, and the whole is 320 tickets, so let p represent the unknown percent.
112 = p(320) If” a = b”,then” ac = bc.
112 ∙ \(\frac{1}{320}\) = p(320) ∙ \(\frac{1}{320}\) “Multiplicative inverse
\(\frac{112}{320}\) = p(1) Multiplicative identity property of 1
\(\frac{7}{20}\) = p
0.35 = p
0.35 = \(\frac{35}{100}\) = 35%, so Haley has made 35% of the tickets for the dance.

We need to know the percent that corresponds with 112, so first we find the percent that corresponds with 1 ticket.
320 → 100%
1 → (\(\frac{100}{320}\))%
112 → 112 ∙ (\(\frac{100}{320}\))%
112 → 112 ∙ (\(\frac{5}{16}\))%
112 → 7∙(5)%
112 → 35%
Haley has made 35% of the tickets for the dance.
Eureka Math Grade 7 Module 4 Lesson 2 Exercise Answer Key
Opening Exercise
a. What is the whole unit in each scenario?
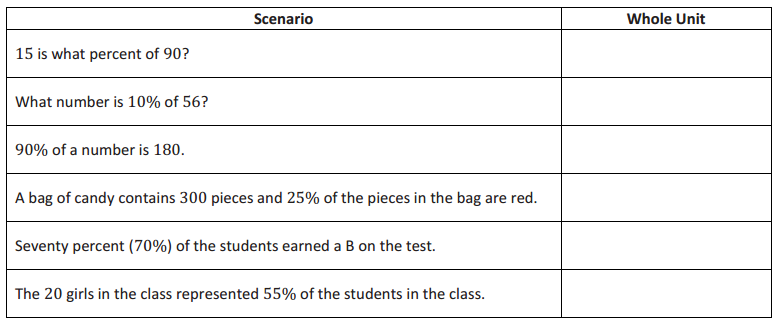
Answer:

b. Read each problem, and complete the table to record what you know.
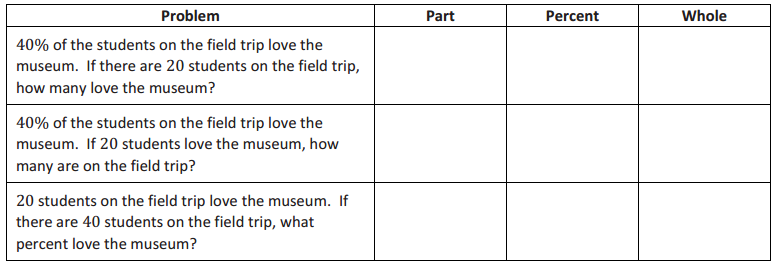
Answer:

Exercise 1.
In Ty’s art class, 12% of the Flag Day art projects received a perfect score. There were 25 art projects turned in by Ty’s class. How many of the art projects earned a perfect score? (Identify the whole.)
Answer:

The whole is the number of art projects turned in by Ty’s class, 25.
\(\frac{25}{100}\) = 0.25; 0.25∙12 = 3; 12% of 25 is 3, so 3 art projects in Ty’s class received a perfect score.
Exercise 2
A bag of candy contains 300 pieces of which 28% are red. How many pieces are not red?
a. Write an equation to represent the number of pieces that are not red, n.
Answer:
Part = Percent×Whole
n = (100% – 28%)(300)
b. Use your equation to find the number of pieces of candy that are not red.
Answer:
If 28% of the candies are red, then the difference of 100% and 28% must be candies that are not red.
n = (100% – 28%)(300)
n = (72%)(300)
n = \(\frac{72}{100}\)(300)
n = 72∙3
n = 216
There are 216 pieces of candy in the bag that are not red.
c. Jah – Lil told his math teacher that he could use the answer from Example 3 and mental math to find the number of pieces of candy that are not red. Explain what Jah – Lil meant by that.
Answer:
He meant that once you know there are 84 red pieces of candy in a bag that contains 300 pieces of candy total, you just subtract 84 from 300 to know that 216 pieces of candy are not red.
Eureka Math Grade 7 Module 4 Lesson 2 Problem Set Answer Key
Question 1.
Represent each situation using an equation. Check your answer with a visual model or numeric method.
a. What number is 40% of 90?
Answer:
n = 0.40(90)
n = 36
b. What number is 45% of 90?
Answer:
n = 0.45(90)
n = 40.5
c. 27 is 30% of what number?
Answer:
27 = 0.3n
\(\frac{27}{0.3}\) = 1n
90 = n
d. 18 is 30% of what number?
Answer:
0.30n = 18
1n = \(\frac{18}{0.3}\)
n = 60
e. 25.5 is what percent of 85?
Answer:
25.5 = p(85)
\(\frac{25.5}{85}\) = 1p
0.3 = p
0.3 = \(\frac{30}{100}\) = 30%
f. 21 is what percent of 60?
21 = p(60)
\(\frac{21}{60}\) = 1p
0.35 = p
0.35 = \(\frac{35}{100}\) = 35%
Question 2.
40% of the students on a field trip love the museum. If there are 20 students on the field trip, how many love the museum?
Answer:
Let s represent the number of students who love the museum.
s = 0.40(20)
s = 8
Therefore, 8 students love the museum.
Question 3.
Maya spent 40% of her savings to pay for a bicycle that cost her $85.
a. How much money was in her savings to begin with?
Answer:
Let s represent the unknown amount of money in Maya’s savings.
85 = 0.4s
212.5 = s
Maya originally had $212.50 in her savings.
b. How much money does she have left in her savings after buying the bicycle?
Answer:
$212.50 – $85.00 = $127.50
She has $127.50 left in her savings after buying the bicycle.
Question 4.
Curtis threw 15 darts at a dartboard. 40% of his darts hit the bull’s – eye. How many darts did not hit the bull’s – eye?
Answer:
Let d represent the number of darts that hit the bull’s – eye.
d = 0.4(15)
d = 6
6 darts hit the bull’s – eye. 15 – 6 = 9
Therefore, 9 darts did not hit the bull’s – eye.
Question 5.
A tool set is on sale for $424.15. The original price of the tool set was $499.00. What percent of the original price is the sale price?
Answer:
Let p represent the unknown percent.
424.15 = p(499)
0.85 = p
The sale price is 85% of the original price.
Question 6.
Matthew scored a total of 168 points in basketball this season. He scored 147 of those points in the regular season and the rest were scored in his only playoff game. What percent of his total points did he score in the playoff game?
Answer:
Matthew scored 21 points during the playoff game because 168 – 147 = 21.
Let p represent the unknown percent.
21 = p(168)
0.125 = p
The points that Matthew scored in the playoff game were 12.5% of his total points scored in basketball this year.
Question 7.
Brad put 10 crickets in his pet lizard’s cage. After one day, Brad’s lizard had eaten 20% of the crickets he had put in the cage. By the end of the next day, the lizard had eaten 25% of the remaining crickets. How many crickets were left in the cage at the end of the second day?
Answer:
Let n represent the number of crickets eaten.
Day 1:
n = 0.2(10)
n = 2
At the end of the first day, Brad’s lizard had eaten 2 of the crickets.
Day 2:
n = 0.25(10 – 2)
n = 0.25(8)
n = 2
At the end of the second day, Brad’s lizard had eaten a total of 4 crickets, leaving 6 crickets in the cage.
Question 8.
A furnace used 40% of the fuel in its tank in the month of March and then used 25% of the remaining fuel in the month of April. At the beginning of March, there were 240 gallons of fuel in the tank. How much fuel (in gallons) was left at the end of April?
Answer:
March:
n = 0.4(240)
n = 96
Therefore, 96 gallons were used during the month of March, which means 144 gallons remain.
April:
n = 0.25(144)
n = 36
Therefore, 36 gallons were used during the month of April, which means 108 gallons remain.
There were 144 gallons of fuel remaining in the tank at the end of March and 108 gallons of fuel remaining at the end of April.
Question 9.
In Lewis County, there were 2,277 student athletes competing in spring sports in 2014. That was 110% of the number from 2013, which was 90% of the number from the year before. How many student athletes signed up for a spring sport in 2012?
Answer:
2013:
2,277 = 1.10a
2,070 = a
Therefore, 2,070 student athletes competed in spring sports in 2013.
2012:
2,070 = 0.9a
2,300 = a
Therefore, 2,300 student athletes competed in spring sports in 2012.
There were 2,070 students competing in spring sports in 2013 and 2,300 students in 2012.
Question 10.
Write a real – world word problem that could be modeled by the equation below. Identify the elements of the percent equation and where they appear in your word problem, and then solve the problem.
57.5 = p(250)
Answer:
Answers will vary. Greig is buying sliced almonds for a baking project. According to the scale, his bag contains 57.5 grams of almonds. Greig needs 250 grams of sliced almonds for his project. What percent of his total weight of almonds does Greig currently have?
The quantity 57.5 represents the part of the almonds that Greig currently has on the scale, the quantity 250 represents the 250 grams of almonds that he plans to purchase, and the variable p represents the unknown percent of the whole quantity that corresponds to the quantity 57.5.
57.5 = p(250)
\(\frac{1}{250}\) (57.5) = p(\(\frac{1}{250}\))(250)
\(\frac{57.5}{250}\) = p(1)
0.23 = p
0.23 = \(\frac{23}{100}\) = 23%
Greig currently has 23% of the total weight of almonds that he plans to buy.
Eureka Math Grade 7 Module 4 Lesson 2 Exit Ticket Answer Key
Question 1.
On a recent survey, 60% of those surveyed indicated that they preferred walking to running.
a. If 540 people preferred walking, how many people were surveyed?
Answer:
Let n represent the number of people surveyed.
0.60n is the number of people who preferred walking.
Since 540 people preferred walking,
0.60n = 540
n = \(\frac{540}{0.6}\) = \(\frac{5,400}{6}\) = 900
Therefore, 900 people were surveyed.
b. How many people preferred running?
Answer:
Subtract 540 from 900.
900 – 540 = 360
Therefore, 360 people preferred running.
Question 2.
Which is greater: 25% of 15 or 15% of 25? Explain your reasoning using algebraic representations or visual models.
Answer:
They are the same.
0.25×15 = \(\frac{25}{100}\) × 15 = 3.75
0.15×25 = \(\frac{15}{100}\) × 25 = 3.75
Also, you can see they are the same without actually computing the product because of any order, any grouping of multiplication.
\(\frac{25}{100}\) × 15 = 25 × \(\frac{1}{100}\) × 15 = 25 × \(\frac{15}{100}\)