Engage NY Eureka Math 7th Grade Module 6 Lesson 11 Answer Key
Eureka Math Grade 7 Module 6 Lesson 11 Exploratory Challenge 1 Answer Key
a. Can any three side lengths form a triangle? Why or why not?
b. Draw a triangle according to these instructions:
✓ Draw segment AB of length 10 cm in your notebook.
✓ Draw segment BC of length 5 cm on one piece of patty paper.
✓ Draw segment AC of length 3 cm on the other piece of patty paper.
✓ Line up the appropriate endpoint on each piece of patty paper with the matching endpoint on segment AB.
✓ Use your pencil point to hold each patty paper in place, and adjust the paper to form △ABC.
c. What do you notice?
d. What must be true about the sum of the lengths of \(\overline{A C}\) and \(\overline{B C}\) if the two segments were to just meet? Use your patty paper to verify your answer.
e. Based on your conclusion for part (d), what if AC = 3 cm as you originally had, but BC = 10 cm. Could you form △ABC?
f. What must be true about the sum of the lengths of \(\overline{A C}\) and \(\overline{B C}\) if the two segments were to meet and form a triangle?
Answer:
a. Possible response: Yes, because a triangle is made up of three side lengths; therefore, any three sides can be put together to form a triangle.
b. 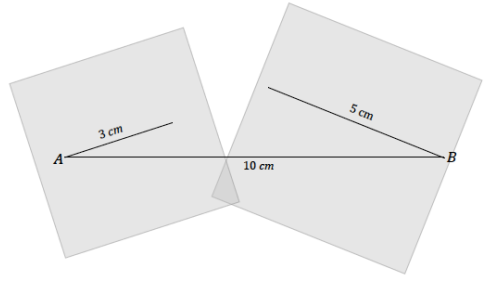
c. △ABC cannot be formed because \(\overline{A C}\) and \(\overline{B C}\) do not meet.
d. For \(\overline{A C}\) and \(\overline{B C}\) to just meet, the sum of their lengths must be equal to 10 cm.
e. △ABC can be formed because \(\overline{A C}\) and \(\overline{B C}\) can meet at an angle and still be anchored at A and B.
f. For \(\overline{A C}\) and \(\overline{B C}\) to just meet and form a triangle, the sum of their lengths must be greater than 10 cm.
Eureka Math Grade 7 Module 6 Lesson 11 Exploratory Challenge 2 Answer Key
a. Which of the following conditions determine a triangle? Follow the instructions to try to draw △ABC. Segment AB has been drawn for you as a starting point in each case.
i) Choose measurements of ∠A and ∠B for △ABC so that the sum of measurements is greater than 180°. Label your diagram.
Your chosen angle measurements: ∠A = ∠B =
Were you able to form a triangle? Why or why not?

ii) Choose measurements of ∠A and ∠B for △ABC so that the measurement of ∠A is supplementary to the measurement of ∠B. Label your diagram.
Your chosen angle measurements: ∠A = ∠B =
Were you able to form a triangle? Why or why not?

iii) Choose measurements of ∠A and ∠B for △ABC so that the sum of measurements is less than 180°. Label your diagram.
Your chosen angle measurements: ∠A = ∠B =
Were you able to form a triangle? Why or why not?

b. Which condition must be true regarding angle measurements in order to determine a triangle?
c. Measure and label the formed triangle in part (a) with all three side lengths and the angle measurement for ∠C. Now, use a protractor, ruler, and compass to draw △A’B’C’ with the same angle measurements but side lengths that are half as long.
d. Do the three angle measurements of a triangle determine a unique triangle? Why or why not?
Answer:
a. i) ∠A = 70° ∠B = 140°
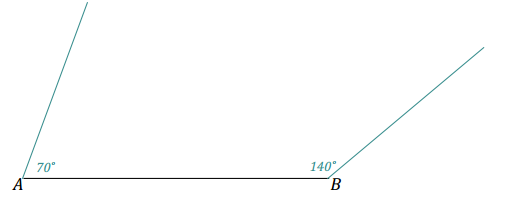
We were not able to form a triangle because the non-horizontal ray of ∠A and the non-horizontal ray of ∠B do not intersect.
ii) ∠A = 40° ∠B = 140°
Selected angle measurements and the corresponding diagram indicate one possible response.
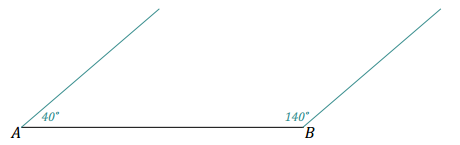
We were not able to form a triangle because the non-horizontal ray of ∠A and the non-horizontal ray of ∠B do not intersect; the non-horizontal rays look parallel.
iii) ∠A = 40° ∠B = 100°
Angle measurements and the corresponding diagram indicate one possible response.
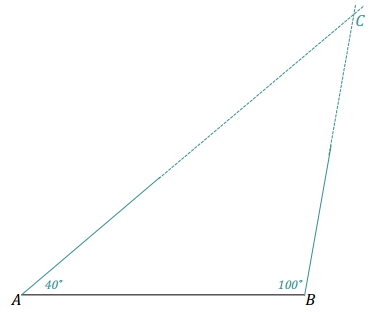
We were able to form a triangle because the non-horizontal ray of ∠A and the non-horizontal ray of ∠B intersect.
b. The sum of two angle measurements of a triangle must be less than 180°.
c. 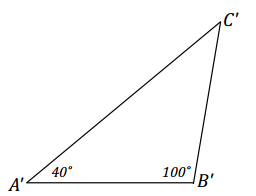
Students should begin by drawing any one side length at a length half as much as the corresponding side in
△ABC and then drawing angles at each end of this line segment. Students should recognize that △A’B’C’ is a scale drawing of △ABC. Ask students to mark all length measurements as a means of verifying that they are indeed half as long as the corresponding sides of the original triangle.
d. Three angles do not determine a unique triangle. For a given triangle with three provided angle measurements, another triangle can be drawn with the same angle measurements but with side lengths proportional to those side lengths of the original triangle.
Eureka Math Grade 7 Module 6 Lesson 11 Exercise Answer Key
Exercise 1.
Two sides of △DEF have lengths of 5 cm and 8 cm. What are all the possible whole number lengths for the remaining side?
Answer:
The possible whole-number side lengths in centimeters are 4, 5, 6, 7, 8, 9, 10, 11, and 12.
Exercise 2.
Which of the following sets of angle measurements determines a triangle?
a. 30°, 120°
b. 125°, 55°
c. 105°, 80°
d. 90°, 89°
e. 91°, 89°
Choose one example from above that does determine a triangle and one that does not. For each, explain why it does or does not determine a triangle using words and a diagram.
Answer:
a. 30°, 120° Determines a triangle
b. 125°, 55° Does not determine a triangle
c. 105°, 80° Does not determine a triangle
d. 90°, 89° Determines a triangle
e. 91°, 89° Does not determine a triangle
Possible response:
The angle measurements in part (a) determine a triangle because the non-horizontal rays of the 30° angle and the 120° angle will intersect to form a triangle
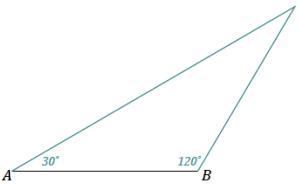
The angle measurements in part (c) do not determine a triangle because the non-horizontal rays of the 105° angle and the 80° angle will not intersect to form a triangle.

Eureka Math Grade 7 Module 6 Lesson 11 Problem Set Answer Key
Question 1.
Decide whether each set of three given lengths determines a triangle. For any set of lengths that does determine a triangle, use a ruler and compass to draw the triangle. Label all side lengths. For sets of lengths that do not determine a triangle, write “Does not determine a triangle,” and justify your response.
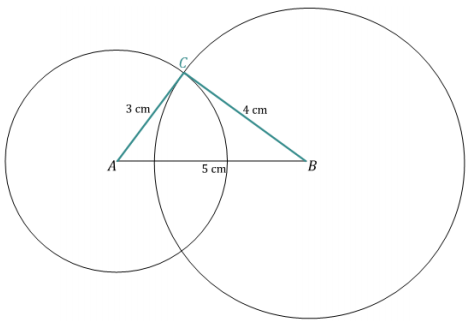
a. 3 cm, 4 cm, 5 cm
b. 1 cm, 4 cm, 5 cm
c. 1 cm, 5 cm, 5 cm
d. 8 cm, 3 cm, 4 cm
e. 8 cm, 8 cm, 4 cm
f. 4 cm, 4 cm, 4 cm
Answer:
a. 3 cm, 4 cm, 5 cm
b. 1 cm, 4 cm, 5 cm
Does not determine a triangle. The shorter lengths are too short to form a triangle. They will only form a segment equal to the length of the longest side.
c. 1 cm, 5 cm, 5 cm
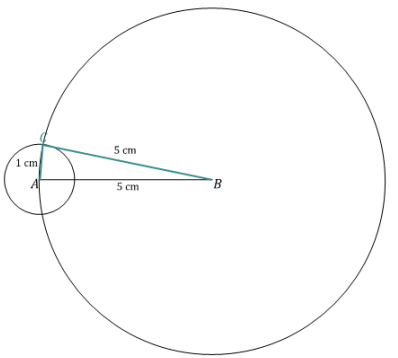
d. 8 cm, 3 cm, 4 cm
Does not determine a triangle. The shorter lengths are too short to form a triangle. They will only form a segment that is shorter than the length of the longest side.
e. 8 cm, 8 cm, 4 cm
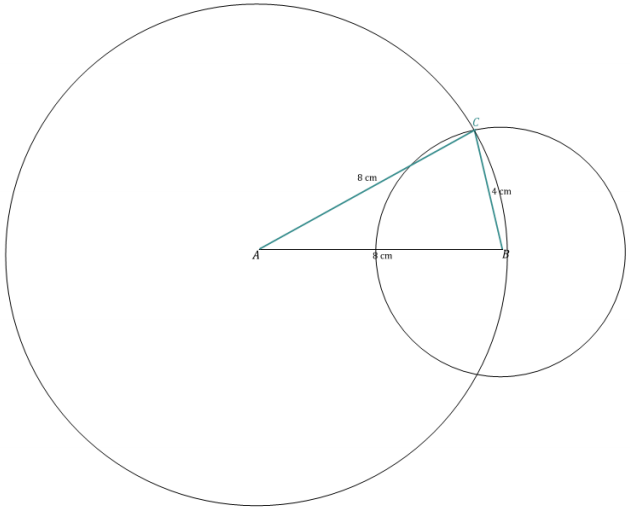
f. 4 cm, 4 cm, 4 cm
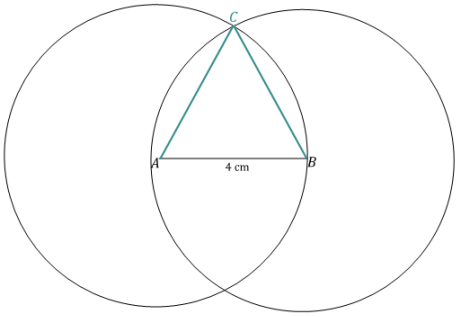
Question 2.
For each angle measurement below, provide one angle measurement that will determine a triangle and one that will not determine a triangle. Provide a brief justification for the angle measurements that will not form a triangle. Assume that the angles are being drawn to a horizontal segment AB; describe the position of the non-horizontal rays of angles ∠A and ∠B.

Answer:
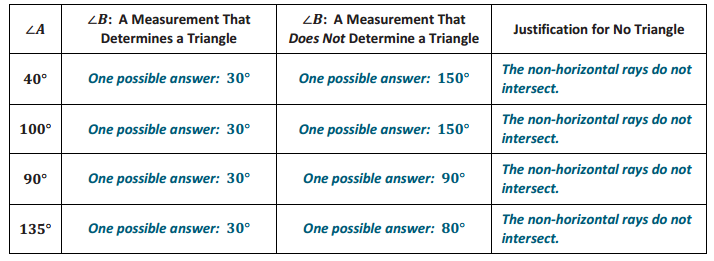
Question 3.
For the given side lengths, provide the minimum and maximum whole number side lengths that determine a triangle.

Answer:
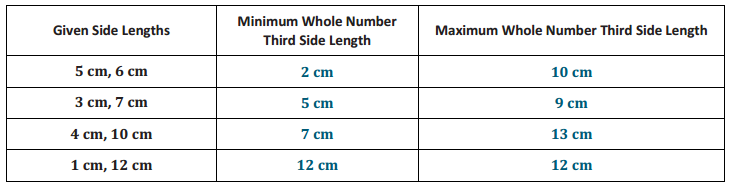
Eureka Math Grade 7 Module 6 Lesson 11 Exit Ticket Answer Key
Question 1.
What is the minimum and maximum whole number side length for △XYZ with given side lengths of 3 cm and 5 cm? Please explain why.
Answer:
Minimum: 3 cm. Maximum: 7 cm. Values above this maximum and below this minimum will not satisfy the condition that the longest side length is less than the sum of the other two side lengths.
Question 2.
Jill has not yet studied the angle measurement requirements to form a triangle. She begins to draw side\(\overline{A B}\) as a horizontal segment of △ABC and considers the following angle measurements for ∠A and ∠B. Describe the
non-horizontal rays in the drawing that results from each set.

a. 45° and 135°
b. 45° and 45°
c. 45° and 145°
Answer:
a. 45° and 135°
The non-horizontal rays of ∠A and ∠B will not intersect to form a triangle; the rays will be parallel to each other.
b. 45° and 45°
The non-horizontal rays of ∠A and ∠B will intersect to form a triangle.
c. 45° and 145°
The non-horizontal rays of ∠A and ∠B will not intersect to form a triangle.