Engage NY Eureka Math 8th Grade Module 7 Lesson 19 Answer Key
Eureka Math Grade 8 Module 7 Lesson 19 Example Answer Key
Example 1.
State as many facts as you can about a cone.
Answer:
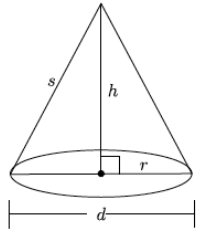
Area of the base:
A = π(r2
Circumference of the base:
C = 2π(r) = π(d)
Volume of the cone:
V = \(\frac{1}{3}\) π(r2)h
Eureka Math Grade 8 Module 7 Lesson 19 Exercise Answer Key
Exercises 1–2
Note: Figures not drawn to scale.
Exercise 1.
Determine the volume for each figure below.
a. Write an expression that shows volume in terms of the area of the base, B, and the height of the figure. Explain the meaning of the expression, and then use it to determine the volume of the figure.
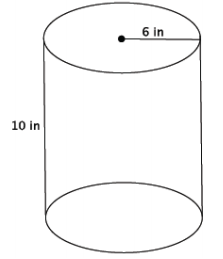
Answer:
The expression V = Bh means that the volume of the cylinder is found by multiplying the area of the base by the height. The base is a circle whose area can be found by squaring the radius, 6 in., and then multiplying by π. The volume is found by multiplying that area by the height of 10.
V = π(6)2 (10)
= 360π
The volume of the cylinder is 360π in3.
b. Write an expression that shows volume in terms of the area of the base, B, and the height of the figure. Explain the meaning of the expression, and then use it to determine the volume of the figure.
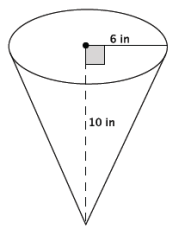
Answer:
V = \(\frac{1}{3}\) Bh
The expression V = \(\frac{1}{3}\) Bh means that the volume of the cone is found by multiplying the area of the base by the height and then taking one-third of that product. The base is a circle whose area can be found by squaring the radius, 6 in., and then multiplying by π. The volume is found by multiplying that area by the height of 10 in. and then taking one-third of that product.
V = \(\frac{1}{3}\) π(6)2 (10)
= \(\frac{360}{3}\) π
= 120 π
The volume of the cone is 120π in3.
Exercise 2.
a. Write an expression that shows volume in terms of the area of the base, B, and the height of the figure. Explain the meaning of the expression, and then use it to determine the volume of the figure.
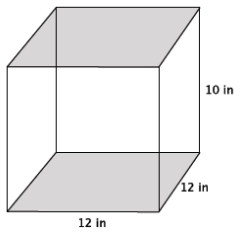
Answer:
V = Bh
The expression V = Bh means that the volume of the prism is found by multiplying the area of the base by the height. The base is a square whose area can be found by multiplying 12×12. The volume is found by multiplying that area, 144, by the height of 10.
V = 12(12)(10)
= 1,440
The volume of the prism is 1,440 in3.
b. The volume of the square pyramid shown below is 480 in3. What might be a reasonable guess for the formula for the volume of a pyramid? What makes you suggest your particular guess?
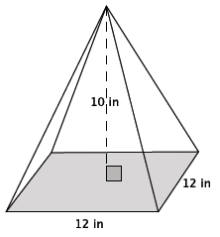
Answer:
Since 480 = \(\frac{1440}{3}\), the formula to find the volume of a pyramid is likely \(\frac{1}{3}\) Bh, where B is the area of the base. This is similar to the volume of a cone compared to the volume of a cylinder with the same base and height. The volume of a square pyramid is \(\frac{1}{3}\) of the volume of the rectangular prism with the same base and height.
Exercises 3–10
Exercise 3.
What is the lateral length (slant height) of the cone shown below?
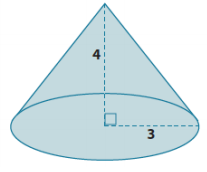
Answer:
Let c be the lateral length.
32 + 42 = c2
9 + 16 = c2
25 = c2
\(\sqrt{25}\) = \(\sqrt{c^{2}}\)
5 = c
The lateral length of the cone is 5 units.
Exercise 4.
Determine the exact volume of the cone shown below.
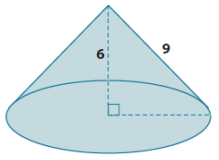
Answer:
Let r be the radius of the base.
62 + r2 = 92
36 + r2 = 81
r2 = 45
The area of the base is 45π units2.
V = \(\frac{1}{3}\) Bh
V = \(\frac{1}{3}\)(45)π(6)
V = 90π
The volume of the cone is 90π units3.
Exercise 5.
What is the lateral length (slant height) of the pyramid shown below? Give an exact square root answer and an approximate answer rounded to the tenths place.
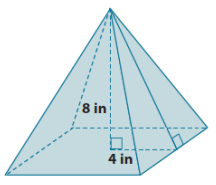
Answer:
Let c in. represent the lateral length of the pyramid.
42 + 82 = c2
16 + 64 = c2
80 = c2
\(\sqrt{80}\) = \(\sqrt{c^{2}}\)
\(\sqrt{80}\) = c
The number \(\sqrt{80}\) is between 8 and 9. In the sequence of tenths, it is between 8.9 and 9.0. Since 80 is closer to 8.92 than 92, the approximate lateral length is 8.9 inches.
Exercise 6.
Determine the volume of the square pyramid shown below. Give an exact answer using a square root.
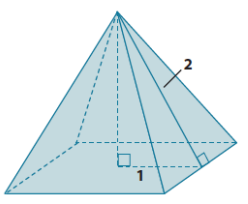
Answer:
Let h be the height of the pyramid.
12 + h2 = 22
1 + h2 = 4
h2 = 3
\(\sqrt{h^{2}}\) = \(\sqrt{3}\)
h = \(\sqrt{3}\)
The area of the base is 4 units2.
V = \(\frac{1}{3}\) (4)(\(\sqrt{3}\))
= \(\frac{4 \sqrt{3}}{3}\)
The volume of the pyramid is \(\frac{4 \sqrt{3}}{3}\) units3.
Exercise 7.
What is the length of the chord of the sphere shown below? Give an exact answer using a square root.
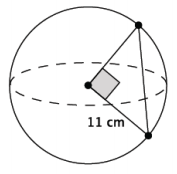
Answer:
Let c cm represent the length of the chord.
112 + 112 = c2
121 + 121 = c2
242 = c2
\(\sqrt{242}\) = \(\sqrt{c^{2}}\)
\(\sqrt{11^{2} \times 2}\) = c
11\(\sqrt{2}\) = c
The length of the chord is \(\sqrt{242}\) cm, or 11\(\sqrt{2}\) cm.
Exercise 8.
What is the length of the chord of the sphere shown below? Give an exact answer using a square root.
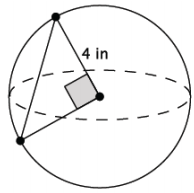
Answer:
Let c in. represent the length of the chord.
42 + 42 = c2
16 + 16 = c2
32 = c2
\(\sqrt{32}\) = \(\sqrt{c^{2}}\)
\(\sqrt{4^{2} \times 2}\) = c
4\(\sqrt{2}\) = c
The length of the chord is \(\sqrt{32}\) in., or 4\(\sqrt{2}\) in.
Exercise 9.
What is the volume of the sphere shown below? Give an exact answer using a square root.
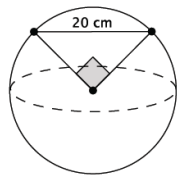
Answer:
Let r cm represent the radius of the sphere.
r2 + r2 = 202
2r2 = 400
r2 = 200
\(\sqrt{r^{2}}\) = \(\sqrt{200}\)
r = \(\sqrt{200}\)
r = \(\sqrt{10^{2} \times 2}\)
r = 10\(\sqrt{2}\)
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(10√2)3
= \(\frac{4}{3}\) π(103 ) (\(\sqrt{2}\))3
= \(\frac{4}{3}\) π(1000)(\(\sqrt{8}\))
= \(\frac{4}{3}\) π(1000)(\(\sqrt{2^{2} \times 2}\))
= \(\frac{4}{3}\) π(1000)(2)(\(\sqrt{2}\))
= \(\frac{8000 \sqrt{2}}{3}\) π
The volume of the sphere is
\(\frac{4000 \sqrt{8}}{3}\) π cm3, or \(\frac{8000 \sqrt{2}}{3}\) π cm3.
Eureka Math Grade 8 Module 7 Lesson 19 Problem Set Answer Key
Question 1.
What is the lateral length (slant height) of the cone shown below? Give an approximate answer rounded to the tenths place.
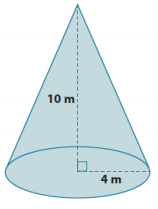
Answer:
Let c m be the lateral length.
102 + 42 = c2
100 + 16 = c2
116 = c2
\(\sqrt{116}\) = \(\sqrt{c^{2}}\)
\(\sqrt{116}\) = c
The number \(\sqrt{116}\) is between 10 and 11. In the sequence of tenths, it is between 10.7 and 10.8. Since 116 is closer to 10.82 than 10.72, the approximate value of the number is 10.8.
The lateral length of the cone is approximately 10.8 m.
Question 2.
What is the volume of the cone shown below? Give an exact answer.
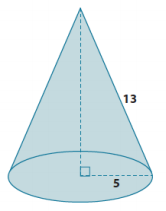
Answer:
Let h represent the height of a cone.
52 + h2 = 132
25 + h2 = 169
h2 = 144
\(\sqrt{h^{2}}\) = \(\sqrt{144}\)
h = 12
The height of the cone is 12 units.
V = \(\frac{1}{3}\) π(25)(12)
= 100π
The volume of the cone is 00π units3.
Question 3.
Determine the volume and surface area of the square pyramid shown below. Give exact answers.
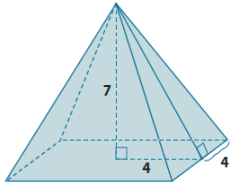
Answer:
V = \(\frac{1}{3}\) (64)(7)
= 448/3
The volume of the pyramid is 448/3 units3.
Let c represent the lateral length.
72 + 42 = c2
49 + 16 = c2
65 = c2
\(\sqrt{65}\) = \(\sqrt{c^{2}}\)
\(\sqrt{65}\) = c
The area of each face of the pyramid is 4\(\sqrt{65}\) units2 (since \(\frac{1}{2}\)×8×\(\sqrt{65}\) = 4\(\sqrt{65}\)), so the area of all four faces is 6\(\sqrt{65}\) units2. Since the base area is 4 units2, the total surface area of the pyramid is (64 + 16\(\sqrt{65}\)) units2.
Question 4.
Alejandra computed the volume of the cone shown below as 64π cm3. Her work is shown below. Is she correct?
If not, explain what she did wrong, and calculate the correct volume of the cone. Give an exact answer.
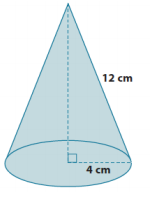
V = \(\frac{1}{3}\) π(42 )(12)
= \(\frac{(16)(12) \pi}{3}\)
= 64π
= 64
Answer:
The volume of the cone is 64π cm3.
Alejandra’s work is incorrect. She used the lateral length instead of the height of the cone to compute volume.
Let h cm represent the height.
42 + h2 = 122
16 + h2 = 144
h2 = 128
\(\sqrt{h^{2}}\) = \(\sqrt{128}\)
h = \(\sqrt{128}\)
h = \(\sqrt{8^{2} \times 2}\)
h = 8\(\sqrt{2}\)
V = \(\frac{1}{3}\) π(4)2 (8\(\sqrt{2}\))
V = \(\frac{1}{3}\) π(128\(\sqrt{65}\))
V = \(\frac{128 \sqrt{2}}{3}\) π
The volume of the cone is \(\frac{128 \sqrt{2}}{3}\) π cm3.
Question 5.
What is the length of the chord of the sphere shown below? Give an exact answer using a square root.
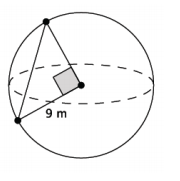
Answer:
Let c m represent the length of the chord.
92 + 92 = c2
81 + 81 = c2
162 = c2
\(\sqrt{162}\) = \(\sqrt{c^{2}}\)
\(\sqrt{162}\) = c
\(\sqrt{9^{2} \times 2}\) = c
9\(\sqrt{2}\) = c
The length of the chord is \(\sqrt{162}\) m, or 9\(\sqrt{2}\) m.
Question 6.
What is the volume of the sphere shown below? Give an exact answer using a square root.
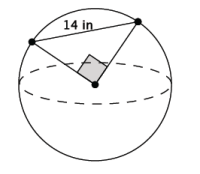
Answer:
Let r in. represent the radius.
r2 + r2 = 142
2r2 = 196
r2 = 98
\(\sqrt{r^{2}}\) = \(\sqrt{98}\)
r = \(\sqrt{7^{2} \times 2}\)
r = 7\(\sqrt{2}\)
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(7\(\sqrt{2}\))3
= \(\frac{4}{3}\) π(343)(\(\sqrt{8}\))
= \(\frac{4}{3}\) π(343)(2\(\sqrt{2}\))
= \(\frac{2744 \sqrt{2}}{3}\) π
The volume of the sphere is \(\frac{4}{3}\) (\(\sqrt{98}\))3 π in3, or \(\frac{2744 \sqrt{2}}{3}\) π in3.
Eureka Math Grade 8 Module 7 Lesson 19 Exit Ticket Answer Key
Question 1.
Which has the larger volume? Give an approximate answer rounded to the tenths place.
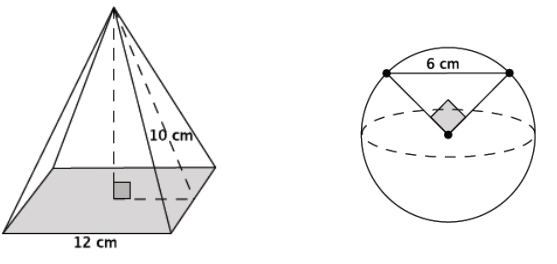
Answer:
Let h cm represent the height of the square pyramid.
h2 + 62 = 102
h2 + 36 = 100
h2 = 64
h = 8
V = \(\frac{1}{3}\) (122)(8)
V = \(\frac{1}{3}\) (144)(8)
V = 384
The volume of the square pyramid is 384 cm3.
Let r represent the radius of the sphere in centimeters.
r2 + r2 = 62
2r2 = 36
r2 = 18
\(\sqrt{r^{2}}\) = \(\sqrt{18}\)
r = \(\sqrt{3^{2} \times 2}\)
r = 3\(\sqrt{2}\)
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(3\(\sqrt{2}\))3
= \(\frac{4}{3}\) π(3)3 (\(\sqrt{2}\))3
= \(\frac{4}{3}\) π(27)(\(\sqrt{8}\))
= \(\frac{4}{3}\) π(27)(\(\sqrt{2^{2} \times 2}\))
= \(\frac{4}{3}\) π(27)(2)(\(\sqrt{2}\))
= 72π\(\sqrt{2}\)
The volume of the sphere is 72π\(\sqrt{2}\) cm3.
The number \(\sqrt{2}\) is between 1 and 2. In the sequence of tenths, it is between 1.4 and 1.5. Since 2 is closer to 1.42 than 1.52, the number is approximately 1.4.
We know from previous lessons we can estimate π = 3.14.
Then, we can calculate the approximate volume of the sphere:
V ≈ (72)(1.4)(3.14)
V ≈ 316.512
The approximate volume of the sphere is 316.512 cm3. Therefore, the volume of the square pyramid is greater.