Engage NY Eureka Math 8th Grade Module 7 Lesson 21 Answer Key
Eureka Math Grade 8 Module 7 Lesson 21 Exercise Answer Key
Exercises 1–4
Exercise 1.
a. Write an expression that can be used to find the volume of the chest shown below. Explain what each part of your expression represents. (Assume the ends of the top portion of the chest are semicircular.)
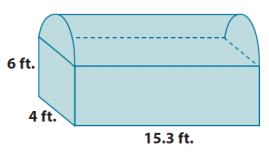
Answer:
(4 × 15.3 × 6) + \(\frac{1}{2}\) (π(2)2 (15.3))
The expression (4 × 15.3 × 6) represents the volume of the prism, and \(\frac{1}{2}\) (π(2)2 (15.3)) is the volume of the half – cylinder on top of the chest. Adding the volumes together will give the total volume of the chest.
b. What is the approximate volume of the chest shown above? Use 3.14 for an approximation of π. Round your final answer to the tenths place.
Answer:
The rectangular prism at the bottom has the following volume:
V = 4 × 15.3 × 6
= 367.2.
The half – cylinder top has the following volume:
V = \(\frac{1}{2}\) (π(2)2 (15.3))
= \(\frac{1}{2}\) (61.2π)
= 30.6π
≈ 96.084.
367.2 + 96.084 = 463.284 ≈ 463.3
The total volume of the chest shown is approximately 463.3 ft3.
Exercise 2.
a. Write an expression for finding the volume of the figure, an ice cream cone and scoop, shown below. Explain what each part of your expression represents. (Assume the sphere just touches the base of the cone.)
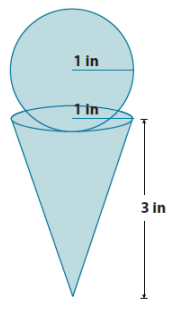
Answer:
\(\frac{4}{3}\) π(1)3 + \(\frac{1}{3}\) π(1)2 (3)
The expression \(\frac{4}{3}\) π(1)3 represents the volume of the sphere, and \(\frac{1}{3}\) π(1)2 (3) represents the volume of the cone. The sum of those two expressions gives the total volume of the figure.
b. Assuming every part of the cone can be filled with ice cream, what is the exact and approximate volume of the cone and scoop? (Recall that exact answers are left in terms of π, and approximate answers use 3.14 for π). Round your approximate answer to the hundredths place.
Answer:
The volume of the scoop is
V = \(\frac{4}{3}\) π(1)3
= \(\frac{4}{3}\) π
≈ 4.19.
The volume of the cone is
V = \(\frac{1}{3}\) π(1)2 (3)
= π
≈ 3.14.
The total volume of the cone and scoop is approximately 4.19 in3 + 3.14 in3, which is 7.33 in3. The exact volume of the cone and scoop is \(\frac{4}{3}\) π in3 + π in3 = \(\frac{7}{3}\) π in3.
Exercise 3.
a. Write an expression for finding the volume of the figure shown below. Explain what each part of your expression represents.
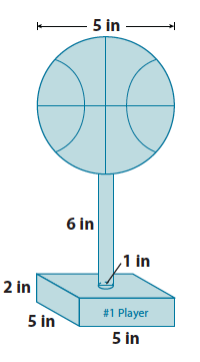
Answer:
(5 × 5 × 2) + π(\(\frac{1}{2}\))2 (6) + \(\frac{4}{3}\) π(2.5)3
The expression (5 × 5 × 2) represents the volume of the rectangular base, π(\(\frac{1}{2}\))2 (6) represents the volume of the cylinder, and \(\frac{4}{3}\) π(2.5)3 is the volume of the sphere on top. The sum of the separate volumes gives the total volume of the figure.
b. Every part of the trophy shown is solid and made out of silver. How much silver is used to produce one trophy? Give an exact and approximate answer rounded to the hundredths place.
Answer:
The volume of the rectangular base is
V = 5 × 5 × 2
= 50.
The volume of the cylinder holding up the basketball is
V = π(\(\frac{1}{2}\))2 (6)
= \(\frac{1}{4}\) π(6)
= \(\frac{3}{2}\) π
≈ 4.71.
The volume of the basketball is
V = \(\frac{4}{3}\) π(2.5)3
= \(\frac{4}{3}\) π(15.625)
= \(\frac{62.5}{3}\) π
≈ 65.42.
The approximate total volume of silver needed is 50 in3 + 4.71 in3 + 65.42 in3, which is 120.13 in3.
The exact volume of the trophy is calculated as follows:
V = 50 in3 + \(\frac{3}{2}\) π in3 + \(\frac{62.5}{2}\) π in3
= 50 in3 + (\(\frac{3}{2}\) + \(\frac{62.5}{2}\))π in3
= 50 in3 + \(\frac{134}{6}\) π in3
= 50 in3 + \(\frac{67}{3}\) π in3.
The exact volume of the trophy is 50 in3 + \(\frac{67}{3}\) π in3.
Exercise 4.
Use the diagram of scoops below to answer parts (a) and (b).
a. Order the scoops from least to greatest in terms of their volumes. Each scoop is measured in inches. (Assume the third scoop is hemi – spherical.).
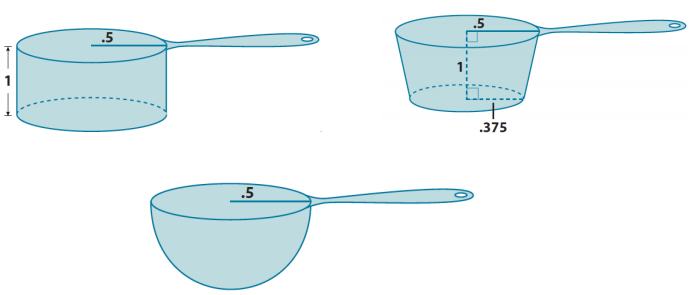
Answer:
The volume of the cylindrical scoop is
V = π(\(\frac{1}{2}\))2 (1)
= \(\frac{1}{4}\) π.
The volume of the spherical scoop is
V = \(\frac{1}{2}\) (\(\frac{4}{3}\) π(\(\frac{1}{2}\))3)
= \(\frac{1}{2}\) (\(\frac{4}{3}\) π(\(\frac{1}{8}\)))
= \(\frac{4}{48}\) π
= \(\frac{1}{12}\) π.
The volume of the truncated cone scoop is as follows.
Let x represent the height of the portion of the cone that was removed.
\(\frac{0.5}{0.375}\) = \(\frac{x + 1}{x}\)
0.5x = 0.375(x + 1)
0.5x = 0.375x + 0.375
0.125x = 0.375
x = 3
The volume of the small cone is
V = \(\frac{1}{3}\) π(0.375)2 (3)
= \(\frac{9}{64}\) π.
The volume of the large cone is
V = \(\frac{1}{3}\) π(0.5)2 (4)
= \(\frac{1}{3}\) π.
The volume of the truncated cone is
\(\frac{1}{3}\) π – \(\frac{9}{64}\) π = (\(\frac{1}{3}\) – \(\frac{9}{64}\))π
= \(\frac{64 – 27}{192}\) π
= \(\frac{37}{192}\)π.
The three scoops have volumes of \(\frac{1}{4}\) π in3, \(\frac{1}{12}\) π in3, and \(\frac{37}{192}\)π in3. In order from least to greatest, they are \(\frac{1}{12}\) π in3, \(\frac{37}{192}\) π in3, and \(\frac{1}{4}\) π in3. Therefore, the spherical scoop is the smallest, followed by the truncated cone scoop, and lastly the cylindrical scoop.
b. How many of each scoop would be needed to add a half – cup of sugar to a cupcake mixture? (One – half cup is approximately 7 in3.) Round your answer to a whole number of scoops.
Answer:
The cylindrical scoop is \(\frac{1}{4}\) π in3, which is approximately 0.785 in3. Let x be the number of scoops needed to fill one – half cup.
0.785x = 7
x = \(\frac{7}{0.785}\)
= 8.9171…
≈ 9
It would take about 9 scoops of the cylindrical cup to fill one – half cup.
The spherical scoop is \(\frac{1}{12}\) π in3, which is approximately 0.262 in3. Let x be the number of scoops needed to fill one – half cup.
0.262x = 7
x = \(\frac{7}{0.262}\)
= 26.71755…
≈ 27
It would take about 27 scoops of the cylindrical cup to fill one – half cup.
The truncated cone scoop is \(\frac{37}{192}\) π in3, which is approximately 0.605 in3. Let x be the number of scoops needed to fill one – half cup.
0.605x = 7
x = \(\frac{7}{0.605}\)
= 11.57024…
≈ 12
It would take about 12 scoops of the cylindrical cup to fill one – half cup.
Eureka Math Grade 8 Module 7 Lesson 21 Problem Set Answer Key
Question 1.
What volume of sand is required to completely fill up the hourglass shown below? Note: 12 m is the height of the truncated cone, not the lateral length of the cone.
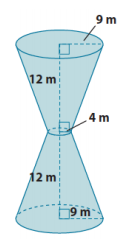
Answer:
Let x m represent the height of the portion of the cone that has been removed.
\(\frac{4}{9}\) = \(\frac{x}{x + 12}\)
4(x + 12) = 9x
4x + 48 = 9x
48 = 5x
\(\frac{48}{5}\) = x
9.6 = x
The volume of the removed cone is
V = \(\frac{1}{3}\) π(4)2 (9.6)
= \(\frac{153.6}{3}\) π.
The volume of the cone is
V = \(\frac{1}{3}\) π(9)2 (21.6)
= \(\frac{1749.6}{2}\) π.
The volume of one truncated cone is
\(\frac{1749.6}{3}\) π – \(\frac{153.6}{3}\) π = (\(\frac{1749.6}{3}\) – \(\frac{153.6}{3}\))π
= \(\frac{1596}{3}\) π
= 532 π.
The volume of sand needed to fill the hourglass is 1064π m3.
Question 2.
a. Write an expression for finding the volume of the prism with the pyramid portion removed. Explain what each part of your expression represents.
(12)3 – 1/3 (12)3
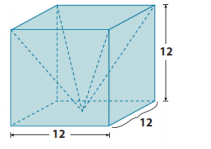
Answer:
The expression (12)3 represents the volume of the cube, and \(\frac{1}{3}\) (12)3 represents the volume of the pyramid. Since the pyramid’s volume is being removed from the cube, we subtract the volume of the pyramid from the volume of the cube.
b. What is the volume of the prism shown above with the pyramid portion removed?
Answer:
The volume of the prism is
V = (12)3
= 1728.
The volume of the pyramid is
V = \(\frac{1}{3}\) (1728)
= 576.
The volume of the prism with the pyramid removed is 1,152 units3.
Question 3.
a. Write an expression for finding the volume of the funnel shown to the right. Explain what each part of your expression represents.
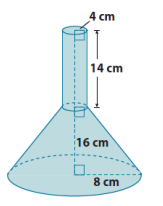
Answer:
π(4)2 (14) + (\(\frac{1}{3}\) π(8)2 (x + 16) – \(\frac{1}{3}\) π(4)2 x)
The expression π(4)2 (14) represents the volume of the cylinder. The expression (\(\frac{1}{3}\) π(8)2 (x + 16) – \(\frac{1}{3}\) π(4)2 x) represents the volume of the truncated cone.
The x represents the unknown height of the smaller cone that has been removed. When the volume of the cylinder is added to the volume of the truncated cone, then we will have the volume of the funnel shown.
b. Determine the exact volume of the funnel.
Answer:
The volume of the cylinder is
V = π(4)2 (14)
= 224π.
Let x cm be the height of the cone that has been removed.
\(\frac{4}{8}\) = \(\frac{x}{x + 16}\)
4(x + 16) = 8x
4x + 64 = 8x
64 = 4x
16 = x
The volume of the small cone is
V = \(\frac{1}{3}\) π(4)2 (16)
= \(\frac{256}{3}\) π.
The volume of the large cone is
V = \(\frac{1}{3}\) π(8)2 (32)
= \(\frac{2048}{2}\) π.
The volume of the truncated cone is
\(\frac{2048}{3}\) π – \(\frac{256}{3}\) π = (\(\frac{2048}{3}\) – \(\frac{256}{3}\))π
= \(\frac{1792}{3}\) π.
The volume of the funnel is 224π cm3 + \(\frac{1792}{3}\) π cm3, which is 821 \(\frac{1}{3}\) π cm3.
Question 4.
What is the approximate volume of the rectangular prism with a cylindrical hole shown below? Use 3.14 for π. Round your answer to the tenths place.
The volume of the prism is
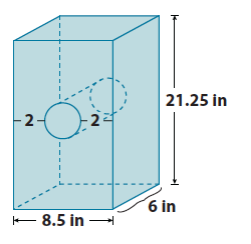
Answer:
V = (8.5)(6)(21.25)
= 1083.75.
The volume of the cylinder is
V = π(2.25)2 (6)
= 30.375π
≈ 95.3775.
The volume of the prism with the cylindrical hole is approximately 988.4 in3, because 1083.75 in3 – 95.3775 in3 = 988.3725 in3.
Question 5.
A layered cake is being made to celebrate the end of the school year. What is the exact total volume of the cake shown below?
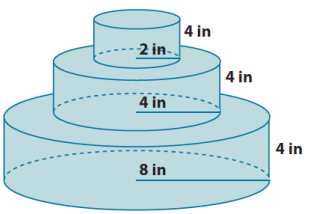
Answer:
The bottom layer’s volume is
V = (8)2 π(4)
= 256π.
The middle layer’s volume is
V = (4)2 π(4)
= 64π.
The top layer’s volume is
V = (2)2 π(4)
= 16π.
The total volume of the cake is
256π in3 + 64π in3 + 16π in3 = (256 + 64 + 16)π in3 = 336π in3.
Eureka Math Grade 8 Module 7 Lesson 21 Exit Ticket Answer Key
Question 1.
Andrew bought a new pencil like the one shown below on the left. He used the pencil every day in his math class for a week, and now his pencil looks like the one shown below on the right. How much of the pencil, in terms of volume, did he use?
Note: Figures are not drawn to scale.

Answer:
V = π(0.375)2 (8)
V = 1.125π
Volume of the pencil at the beginning of the week was 1.125π in3.
V = π(0.375)2 (2.5)
V ≈ 0.3515π
The volume of the cylindrical part of the pencil is approximately 0.3515π in3.
V = \(\frac{1}{3}\) π(0.375)2 (0.75)
V ≈ \(\frac{0.1054}{3}\) π
V ≈ 0.0351π
The volume of the cone part of the pencil is approximately 0.0351π in3.
0.3515π + 0.0351π = (0.3515 + 0.0351)π = 0.3866π
The total volume of the pencil after a week is approximately 0.3866π in3.
1.125π – 0.3866π = (1.125 – 0.3866)π = 0.7384π
In one week, Andrew used approximately 0.7384π in3 of the pencil’s total volume.