Engage NY Eureka Math Precalculus Module 1 Lesson 19 Answer Key
Eureka Math Precalculus Module 1 Lesson 19 Example Answer Key
Example:
Find the Two Square Roots of a Complex Number
Find both of the square roots of -2-2\(\sqrt{3}\)i.
Answer:
The polar form of this number is 4(cos(\(\frac{4π}{3}\))+i sin(\(\frac{4π}{3}\))). The square roots of this number will have modulus \(\sqrt{4}\)=2 and arguments given by α=\(\frac{θ}{n}\)+\(\frac{2πk}{n}\) for k=0,1 where θ=\(\frac{4π}{3}\). Thus,
α=\(\frac{1}{2}\) (\(\frac{4π}{3}\)+2π∙0)=\(\frac{2π}{3}\)
and
α=\(\frac{1}{2}\) (\(\frac{4π}{3}\)+2π∙1)=\(\frac{5π}{3}\)
The square roots are
2(cos(\(\frac{2π}{3}\))+i sin(\(\frac{2π}{3}\)) )=-1+\(\sqrt{3}\)i
and
2(cos(\(\frac{5π}{3}\))+i sin(\(\frac{5π}{3}\)) )=1-\(\sqrt{3}\)i.
Have students go back and add the graph of the second square root to the graph at the beginning of Exercise 1.
Eureka Math Precalculus Module 1 Lesson 19 Exercise Answer Key
Opening Exercise
A polar grid is shown below. The grid is formed by rays from the origin at equal rotation intervals and concentric circles centered at the origin. The complex number z=\(\sqrt{3}\)+i is graphed on this polar grid.
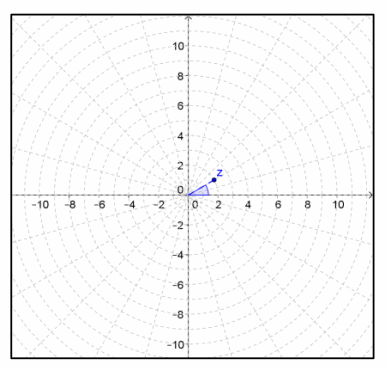
a. Use the polar grid to identify the modulus and argument of z.
Answer:
The argument is \(\frac{\pi}{6}\), and the modulus is 2.
b. Graph the next three powers of z on the polar grid. Explain how you got your answers.
Answer:
Each power of z is another 30° rotation and a dilation by a factor of 2 from the previous number.
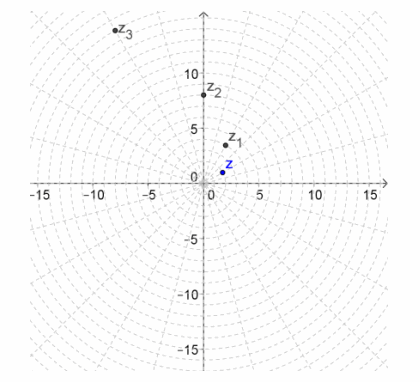
c. Write the polar form of the number in the table below, and then rewrite it in rectangular form.

Answer:

Have early finishers check their work by calculating one or two powers of z by expanding and then multiplying the rectangular form. Examples are shown below.
(\(\sqrt{3}\)+i)2=3+2\(\sqrt{3}\)i+i2=2+2\(\sqrt{3}\)i
(\(\sqrt{3}\)+i)\(\sqrt{3}\)=(\(\sqrt{3}\)+i)(2+2\(\sqrt{3}\)i)=2\(\sqrt{3}\)+6i+2i+2\(\sqrt{3}\)i2=8i
Debrief by having one or two students explain their process to the class. Remind them again of the efficiency of working with complex numbers in polar form and the patterns that emerge when they graph powers of a complex number.
→ Which way of expanding a power of a complex number would be quicker if you were going to expand
(\(\sqrt{3}\)+i)10?
→ Using the polar form would be far easier. It would be 210 (cos(\(\frac{5π}{3}\))+i sin(\(\frac{5π}{3}\)) )ow could you describe the pattern of the numbers if we continued graphing the powers of z?
→ The numbers are spiraling outward as each number is on a ray rotated 30° from the previous one and farther from the origin by a factor of 2.
Next, transition to the main focus of this lesson by giving students time to consider the next question. Have them respond in writing and discuss their answers with a partner.
→ How do you think we could reverse this process, in other words, undo squaring a complex number or undo cubing a complex number?
→ That would be like taking a square root or cube root. We would have to consider how to undo the rotation and dilation effects.
Exercises 1–3
The complex numbers z2=(-1+\(\sqrt{3}\)i)2 and z1 are graphed below.
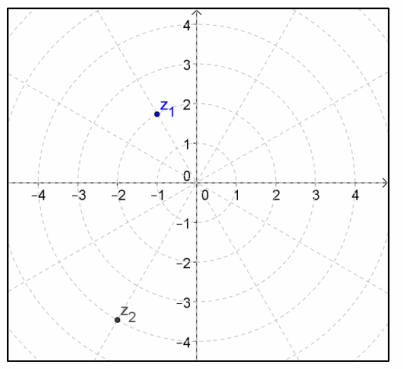
Exercise 1.
Use the graph to help you write the numbers in polar and rectangular form.
Answer:
z1=2(cos(\(\frac{2π}{3}\))+i sin(\(\frac{2π}{3}\)) )=-1+\(\sqrt{3}\)i
z2=4(cos(\(\frac{4π}{3}\))+i sin(\(\frac{4π}{3}\)) )=-2-2\(\sqrt{3}\)i
Exercise 2.
Describe how the modulus and argument of z1=-1+\(\sqrt{3}\)i are related to the modulus and argument of
z2=(-1+\(\sqrt{3}\)i)2.
Answer:
The modulus and argument are both cut in half.
Exercise 3.
Why could we call -1+\(\sqrt{3}\)i a square root of -2-2\(\sqrt{3}\)i?
Answer:
Clearly, (-1+\(\sqrt{3}\)i)2=-2-2\(\sqrt{3}\). We can demonstrate this using the rectangular or polar form and verify it using transformations of the numbers when they are plotted in the complex plane. So, it would make sense then that raising both sides of this equation to the \(\frac{1}{2}\) power should give us the desired result.
Start with the equation, (-1+\(\sqrt{3}\)i)2=-2-2\(\sqrt{3}\)i.
((-1+\(\sqrt{3}\)i)2)\(\frac{1}{2}\)=(-2-2\(\sqrt{3}\)i)\(\frac{1}{2}\)
-1+\(\sqrt{3}\)i=\(\sqrt{-2-2 \sqrt{3} i}\))
Alternately, using the formula from Lesson 17, replace n with \(\frac{1}{2}\).
zn=rn (cos(nθ)+i sin(nθ))
z\(\frac{1}{2}\)=r\(\frac{1}{2}\) (cos(\(\frac{1}{2}\) θ)+i sin(\(\frac{1}{2}\)θ))
So, a square root of -2-2\(\sqrt{3}\)i would be
4\(\frac{1}{2}\) (cos(\(\frac{1}{2}\)∙\(\frac{4π}{3}\))+i sin(\(\frac{1}{2}\)∙\(\frac{4π}{3}\)) )=2(cos(\(\frac{2π}{3}\))+i sin(\(\frac{2π}{3}\)) )=-1+\(\sqrt{3}\)i.
After giving students a few minutes to work these exercises with a partner, make sure they understand that the modulus is cut in half because 2∙2=4 shows a repeated multiplication by 2.
→ How would this problem change if the modulus was 9 instead of 4? How would this problem change if the modulus was 3 instead of 4?
→ The new modulus would have to be a number that when squared equals 9, so we would need the new modulus to be the square root of the original modulus.
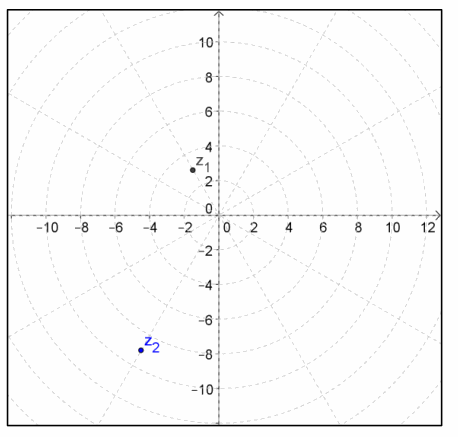
If students seem to think that the modulus would always be divided by 2 instead of it being the square root of the original modulus, model this using Geogebra. A sample screenshot is provided below showing a complex number with the same argument and a modulus of 9. Notice that the modulus of z1 is 3 while the argument is still cut in half.
Exercises 4–6
Exercise 4.
Find the cube roots of -2=2\(\sqrt{3}\)i.
Answer:
-2-2\(\sqrt{3}\)i=4(cos(\(\frac{4π}{3}\))+i sin(\(\frac{4π}{3}\)))
The modulus of the cube roots will be \(\sqrt[3]{4}\). The arguments for k=0, 1, and 2 are given by α=\(\frac{θ}{n}\)+\(\frac{2πk}{n}\)where
θ=\(\frac{4π}{3}\) and n=3. Using this formula, the arguments are \(\frac{4π}{9}\), \(\frac{10π}{9}\), and \(\frac{16π}{9}\). The three cube roots of -2-2\(\sqrt{3}\)i are
\(\sqrt[3]{4}\)(cos(\(\frac{4π}{9}\))+i sin(\(\frac{4π}{9}\)))
\(\sqrt[3]{4}\)(cos(\(\frac{10π}{9}\))+i sin(\(\frac{10π}{9}\)))
\(\sqrt[3]{4}\)(cos(\(\frac{16π}{9}\))+i sin(\(\frac{16π}{9}\)))
Exercise 5.
Find the square roots of 4i.
Answer:
4i=4(cos(\(\frac{π}{2}\))+i sin(\(\frac{π}{2}\)) )
The modulus of the square roots is \(\sqrt{4}\)=2. The arguments for k=0 and 1 are given by α=\(\frac{θ}{n}\)+\(\frac{2πk}{n}\) where θ=\(\frac{π}{2}\)
and n=2. Using this formula, the arguments are \(\frac{π}{4}\) and \(\frac{3π}{4}\). The two square roots of 4i are
2(cos(\(\frac{π}{4}\))+i sin(\(\frac{π}{4}\)) )=\(\sqrt{2}\)+\(\sqrt{2}\) i
and
2(cos(\(\frac{3π}{4}\))+i sin(\(\frac{3π}{4}\)) )=-\(\sqrt{2}\)+\(\sqrt{2}\)i.
Exercise 6.
Find the cube roots of 8.
Answer:
In polar form,
8=8(cos(0)+i sin(0) ).
The modulus of the cube roots is √(3&8)=2. The arguments for k=0, 1, and 2 are given by α=\(\frac{θ}{n}\)+\(\frac{2πk}{n}\) where
θ=0 and n=3. Using this formula, the arguments are 0, \(\frac{2π}{3}\), and \(\frac{4π}{3}\). The three cube roots of 8 are
2(cos(0)+i sin(0) )=2
2(cos(\(\frac{2π}{3}\))+i sin(\(\frac{2π}{3}\)) )=-1+\(\sqrt{3}\)i
2(cos(\(\frac{4π}{3}\))+i sin(\(\frac{4π}{3}\)) )=-1-\(\sqrt{3}\)i
Consider pointing out to students that the answers to Exercise 9 are the solutions to the equation x\(\sqrt{3}\)-8=0.
x\(\sqrt{3}\)-8=0
(x-2)(x2+2x+4)=0
One solution is -2, and the other two are solutions to x2+2x+4=0. Using the quadratic formula, the other two solutions are given by
x=\(\frac{-2 \pm \sqrt{2^{2}-4(1)(4)}}{2}\).
This expression gives the solutions -1+\(\sqrt{3}\)i and -1-\(\sqrt{3}\)i. This connection with the work in Algebra II, Module 2 is revisited in the last few exercises in the Problem Set.
Eureka Math Precalculus Module 1 Lesson 19 Problem Set Answer Key
Question 1.
For each complex number, what is z2?
a. 1+\(\sqrt{3}\)i
Answer:
-2+2\(\sqrt{3}\)i
b. 3-3i
Answer:
-18i
c. 4i
Answer:
-16
d. –\(\frac{\sqrt{3}}{2}\)+\(\frac{1}{2}\)i
Answer:
\(\frac{1}{2}\)–\(\frac{\sqrt{3}}{2}\)i
e. \(\frac{1}{9}\)+\(\frac{1}{9}\) i
Answer:
\(\frac{2}{81}\)i
f. -1
Answer:
1
Question 2.
For each complex number, what are the square roots of z?
a. 1+\(\sqrt{3}\)i
Answer:
z=1+\(\sqrt{3}\)i,r=2,arg(z)=\(\frac{π}{3}\),
α=\(\frac{1}{2}\) (\(\frac{π}{3}\)+2πk),k=0 or 1 α=\(\frac{π}{6}\) or \(\frac{7π}{6}\) Let the square roots of z be w1 and w2.
w1=\(\sqrt{2}\) (cos \(\frac{π}{6}\)+i∙sin \(\frac{π}{6}\))=\(\sqrt{2}\) (\(\frac{\sqrt{3}}{2}\)+\(\frac{1}{2}\)i)
w2=\(\sqrt{2}\) (cos \(\frac{7π}{6}\)+i∙sin \(\frac{7π}{6}\))=\(\sqrt{2}\) (-\(\frac{\sqrt{3}}{2}\)–\(\frac{1}{2}\)i)
b. 3-3i
Answer:
z=3-3i,r=\(\sqrt{18}\),arg(z)=\(\frac{7π}{4}\),
α=\(\frac{1}{2}\) (\(\frac{7π}{4}\)+2πk),k=0 or 1 α=\(\frac{7π}{8}\) or \(\frac{15π}{8}\) Let the square roots of z be w1 and w2.
w1=\(\sqrt[4]{18}\)(cos \(\frac{7π}{8}\)+i∙sin \(\frac{7π}{8}\))
w2=\(\sqrt[4]{18}\)(cos \(\frac{15π}{8}\)+i∙sin \(\frac{15π}{8}\))
c. 4i
Answer:
z=0+4i,r=4,arg(z)=\(\frac{π}{2}\),
α=\(\frac{1}{2}\) (\(\frac{π}{2}\)+2πk),k=0 or 1 α=\(\frac{π}{4}\) or 5\(\frac{π}{4}\) Let the square roots of z be w1 and w2.
w1=\(\sqrt{4}\) (cos \(\frac{π}{4}\)+i∙sin \(\frac{π}{4}\))=2(\(\frac{\sqrt{2}}{2}\)+\(\frac{\sqrt{2}}{2}\) i)=\(\sqrt{2}\)+\(\sqrt{2}\) i
w2=\(\sqrt{4}\) (cos \(\frac{5π}{4}\)+i∙sin \(\frac{5π}{4}\))=2(-\(\frac{\sqrt{2}}{2}\)+(-\(\frac{\sqrt{2}}{2}\) i)=-\(\sqrt{2}\)–\(\sqrt{2}\) i
d. –\(\frac{\sqrt{3}}{2}\)+\(\frac{1}{2}\)i
Answer:
z=(-\(\frac{\sqrt{3}}{2}\)+\(\frac{1}{2}\)i,r=1,arg(z)=\(\frac{5π}{6}\),
α=\(\frac{1}{2}\) (\(\frac{5π}{6}\)+2πk),k=0 or 1 α=\(\frac{5π}{12}\) or \(\frac{17π}{12}\) Let the square roots of z be w1 and w2.
w1=\(\sqrt{1}\)(cos \(\frac{5π}{12}\)+i∙sin \(\frac{5π}{12}\))=cos \(\frac{5π}{12}\)+i∙sin \(\frac{5π}{12}\)
w2=\(\sqrt{1}\)(cos \(\frac{5π}{12}\)+i∙sin \(\frac{5π}{12}\))=cos \(\frac{17π}{12}\)+i∙sin \(\frac{17π}{12}\)
e. \(\frac{1}{9}\)+\(\frac{1}{9}\) i
Answer:
z=\(\frac{1}{9}\)+\(\frac{1}{9}\) i,r=\(\frac{\sqrt{2}}{9}\),arg(z)=\(\frac{π}{4}\),
α=\(\frac{1}{2}\)(\(\frac{π}{4}\)+2πk),k=0 or 1 α=\(\frac{π}{8}\) or 9\(\frac{π}{8}\) Let the square roots of z be w1 and w2.
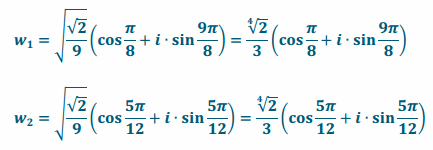
f. -1
Answer:
z=-1+0i, r=1, arg(z)=π
α=\(\frac{1}{2}\) (π+2πk), k=0 or 1 α=\(\frac{π}{2}\) or \(\frac{3π}{2}\) Let the square roots of z be w1 and w2.
w1=1(cos \(\frac{π}{2}\)+i∙sin \(\frac{π}{2}\))=i
w2=1(cos 3\(\frac{π}{2}\)+i∙sin 3\(\frac{π}{2}\))=-i
Question 3.
Graph each complex number on a polar grid.
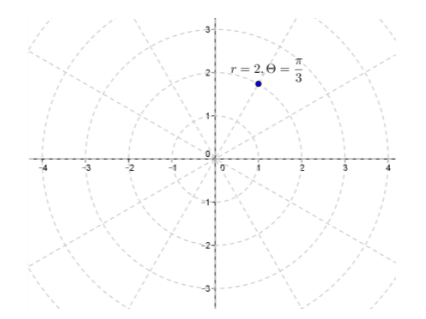
a. 2(cos(\(\frac{π}{3}\))+i sin(\(\frac{π}{3}\)) )
Answer:
r=2,θ=\(\frac{π}{3}\)
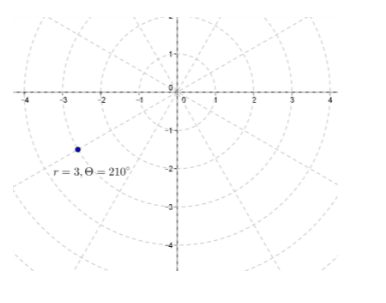
b. 3(cos(210°)+i sin(210°) )
Answer:
r=3,θ=210°
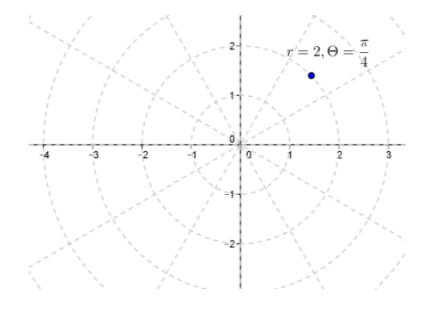
c. 2(cos(\(\frac{π}{4}\))+i sin(\(\frac{π}{4}\)) )
Answer:
r=2,θ=\(\frac{π}{4}\)
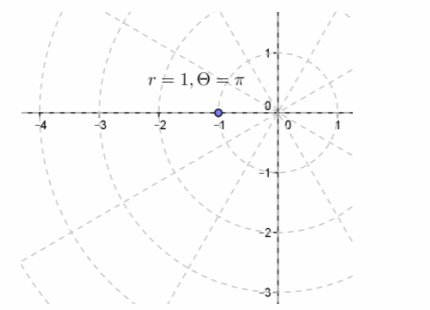
d. cos(π)+i sin(π)
Answer:
r=1,θ=π
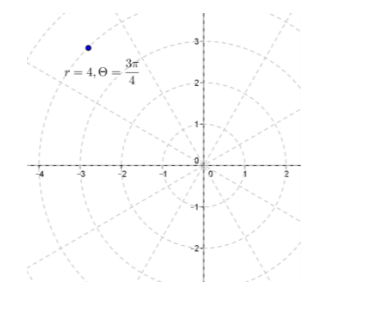
e. 4(cos(\(\frac{3π}{4}\))+i sin(\(\frac{3π}{4}\)) )
Answer:
r=4,θ=\(\frac{3π}{4}\)
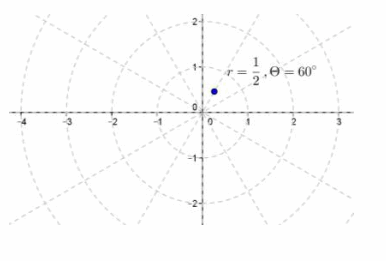
f. \(\frac{1}{2}\) (cos(60°)+i sin(60°) )
Answer:
r=\(\frac{1}{2}\),θ=60°
Question 4.
What are the cube roots of –3i?
Answer:
z=0-3i,r=3,arg(z)=\(\frac{3π}{2}\),
α=\(\frac{1}{3}\)(\(\frac{3π}{2}\)+2πk),k=0,1, or 2 α=\(\frac{π}{2}\),\(\frac{7π}{6}\) or \(\frac{11π}{6}\) Let the cube roots of z be w1, w2, and w3.
w1=\(\sqrt[3]{3}\)(cos \(\frac{π}{2}\)+i∙sin \(\frac{π}{2}\))=\(\sqrt[3]{3}\)(0+i)=\(\sqrt[3]{3}\)∙i
w2=\(\sqrt[3]{3}\)(cos \(\frac{7π}{6}\)+i∙sin \(\frac{7π}{6}\))=\(\sqrt[3]{3}\)((-\(\frac{\sqrt{3}}{2}\)–\(\frac{1}{2}\)i)
w3=\(\sqrt[3]{3}\)(cos \(\frac{11π}{6}\)+i∙sin \(\frac{11π}{6}\))=\(\sqrt[3]{3}\)(\(\frac{\sqrt{3}}{2}\)–\(\frac{1}{2}\)i)
Question 5.
What are the fourth roots of 64?
Answer:
z=64+0i,r=64,arg(z)=0,
α=\(\frac{1}{4}\)(0+2πk),k=0,1,2, or 3 α=0,\(\frac{π}{2}\),π, or 3\(\frac{π}{2}\) Let the fourth roots of z be w1, w2, w3, and w4.
w1=\(\sqrt[4]{64}\)(cos0+i∙sin0)=2\(\sqrt{2}\) (1+0)=2\(\sqrt{2}\)
w2=\(\sqrt[4]{64}\)(cos \(\frac{π}{2}\),+i∙sin \(\frac{π}{2}\))=2\(\sqrt{2}\) (0+i)=2\(\sqrt{2}\)∙i
w3=\(\sqrt[4]{64}\)(cosπ+i∙sinπ)=2\(\sqrt{2}\) (-1+0)=-2\(\sqrt{2}\)
w4=\(\sqrt[4]{64}\)(cos \(\frac{3π}{2}\)+i∙sin \(\frac{3π}{2}\))=2\(\sqrt{2}\) (0-i)=-2\(\sqrt{2}\)∙i
Question 6.
What are the square roots of -4-4i?
Answer:
z=-4-4i,r=4\(\sqrt{2}\),arg(z)=5\(\frac{π}{4}\),
α=\(\frac{1}{2}\) (\(\frac{5π}{4}\)+2πk),k=0 or 1 α=\(\frac{5π}{8}\),π, or \(\frac{13π}{8}\) Let the square roots of z be w1 and w2.
w1=\(2 \sqrt[4]{2}\)(cos \(\frac{5π}{8}\)+i∙sin \(\frac{5π}{8}\))
w2=\(2 \sqrt[4]{2}\)(cos \(\frac{13π}{8}\)+i∙sin \(\frac{13π}{8}\))
Question 7.
Find the square roots of -5. Show that the square roots satisfy the equation x2+5=0.
Answer:
z=-5+0i,r=5,arg(z)=π,
α=\(\frac{1}{2}\) (π+2πk),k=0 or 1 α=\(\frac{π}{2}\) or \(\frac{3π}{2}\) Let the square roots of z be w1 and w2.
w1=\(\sqrt{5}\)(cos \(\frac{π}{2}\)+i∙sin\(\frac{π}{2}\))=\(\sqrt{5}\)(0+i)=\(\sqrt{5}\)∙i
w2=\(\sqrt{5}\)(cos \(\frac{3π}{2}\)+i∙sin \(\frac{3π}{2}\))=\(\sqrt{5}\)(0-i)=-\(\sqrt{5}\)∙i
(\(\sqrt{5}\)∙i)2+5=-5+5=0
(-\(\sqrt{5}\)∙i)2+5=-5+5=0
Question 8.
Find the cube roots of 27. Show that the cube roots satisfy the equation x\(\sqrt{3}\)-27=0.
Answer:
z=27+0i,r=27,arg(z)=0,
α=\(\frac{1}{3}\)(0+2πk),k=0,1, or 2 α=0,\(\frac{2π}{3}\) or \(\frac{4π}{3}\) Let the cube roots of z be w1, w2, and w3.
w1=\(\sqrt[3]{27}\)(cos0+i∙sin)=3(1+0)=3
w2=\(\sqrt[3]{27}\)(cos \(\frac{2π}{3}\)+i∙sin\(\frac{2π}{3}\))=3(-\(\frac{1}{2}\)+\(\frac{\sqrt{3}}{2}\)i)=-\(\sqrt[3]{2}\)+\(\frac{3 \sqrt{3}}{2}\) i
w3=\(\sqrt[3]{27}\)(cos \(\frac{4π}{3}\)+i∙sin \(\frac{4π}{3}\))=3(-\(\frac{1}{2}\)–\(\frac{\sqrt{3}}{2}\)i)=-\(\sqrt[3]{2}\)-(\(\frac{3 \sqrt{3}}{2}\)i
(3)3-27=0
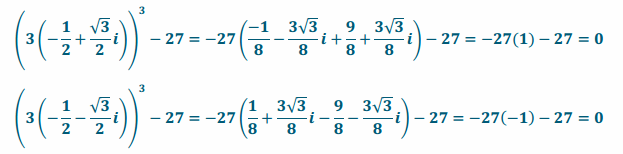
Eureka Math Precalculus Module 1 Lesson 19 Exit Ticket Answer Key
Find the fourth roots of -2-2\(\sqrt{3}\)i.
Answer:
The modulus is 4, and the argument is \(\frac{4π}{3}\). Using the formula, the modulus of the fourth roots will be \(\sqrt[4]{4}\), and the arguments will be \(\frac{1}{4}\)(\(\frac{4π}{3}\))+\(\frac{1}{4}\)(2πk) for k=0,1,2,3. This gives the following complex numbers as the fourth roots of -2-2\(\sqrt{3}\)i.
\(\sqrt[4]{4}\)(cos(\(\frac{π}{3}\))+isin(\(\frac{π}{3}\)) )=\(\sqrt[4]{4}\)(\(\frac{1}{2}\)+\(\frac{\sqrt{3}}{2}\)i)
\(\sqrt[4]{4}\)(cos(\(\frac{5π}{6}\))+i sin(\(\frac{5π}{6}\)) )=\(\sqrt[4]{4}\)(-\(\frac{\sqrt{3}}{2}\)+\(\frac{1}{2}\)i)
\(\sqrt[4]{4}\)(cos(\(\frac{4π}{3}\))+isin(\(\frac{4π}{3}\)) )=\(\sqrt[4]{4}\)(-\(\frac{1}{2}\)–\(\frac{\sqrt{3}}{2}\)i)
\(\sqrt[4]{4}\)(cos(\(\frac{11π}{6}\))+isin(\(\frac{11π}{6}\)) )=\(\sqrt[4]{4}\)(\(\frac{\sqrt{3}}{2}\)–\(\frac{1}{2}\)i)