Engage NY Eureka Math Precalculus Module 1 Lesson 26 Answer Key
Eureka Math Precalculus Module 1 Lesson 26 Exercise Answer Key
Opening Exercise
Perform the following matrix operations:
a. \(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\left[\begin{array}{c}
-1 \\
3
\end{array}\right]\)
Answer:
\(\left[\begin{array}{l}
-9 \\
14
\end{array}\right]\)
b. \(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
\(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\)
c. \(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\left[\begin{array}{cc}
1 & -3 \\
2 & 4
\end{array}\right]\)
Answer:
\(\left[\begin{array}{cc}
-1 & -17 \\
11 & 17
\end{array}\right]\)
d. \(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\)
Answer:
\(\left[\begin{array}{ll}
3 a-2 c & 3 b-2 d \\
1 a+5 c & 1 b+5 d
\end{array}\right]\)
e. \(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\) + \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
\(\left[\begin{array}{cc}
4 & -2 \\
1 & 6
\end{array}\right]\)
f. \(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\) + \(\left[\begin{array}{cc}
1 & -3 \\
2 & 4
\end{array}\right]\)
Answer:
\(\left[\begin{array}{cc}
4 & -5 \\
3 & 9
\end{array}\right]\)
g. \(\left[\begin{array}{cc}
3 & -2 \\
1 & 5
\end{array}\right]\) + \(\left[\begin{array}{ll}
\boldsymbol{a} & \boldsymbol{b} \\
\boldsymbol{c} & \boldsymbol{d}
\end{array}\right]\)
Answer:
\(\left[\begin{array}{cc}
3+a & -2+b \\
1+c & 5+d
\end{array}\right]\)
h. Can you add the two matrices in part (a)? Why or why not?
Answer:
No, the matrices do not have the same dimensions, so they cannot be added.
Exercises
Exercise 1.
Perform the transformation \(\) on the unit square.
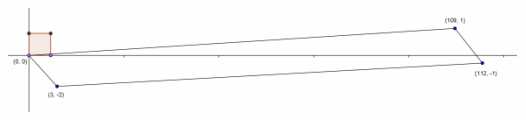
a. Sketch the image. What is the shape of the image?
Answer:
The image is a parallelogram.
b. What are the coordinates of the vertices of the image?
Answer:
(0,0),(3,-2),(109,1), and (112,-1)
c. What is the area of the image? Show your work.
Answer:
Area=|(109)(-2)-(3)(1)|=|-221|=221
Exercise 2.
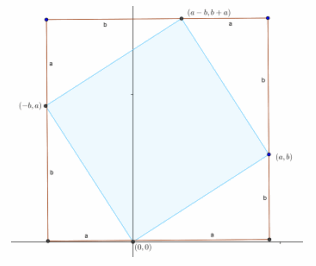
In the Exploratory Challenge, we drew the image of a general rotation/dilation of the unit square \(\).
a. Calculate the area of the image by enclosing the image in a rectangle and subtracting the area of the surrounding right triangles. Show your work.
Answer:
Area=(a+b)2-4(\(\frac{1}{2}\) ab)
Area=a2+2ab+b2-2ab
Area=a2+b2
b. Confirm the area using the determinant of the resulting matrix.
Answer:
\(\left[\begin{array}{cc}
\boldsymbol{a} & -\boldsymbol{b} \\
\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]\)
Area=|(a)(a)-(b)(-b)|=a2+b2
Exercise 3.
We have looked at several general matrix transformations in Module 1. Answer the questions below about these familiar matrices, and explain your answers.
a. What effect does the identity transformation have on the unit square? What is the area of the image? Confirm your answer using the determinant.
Answer:
The identity transformation does nothing to the unit square. The area is 1, as is the determinant of the unit matrix.
b. How does a dilation with a scale factor of k change the area of the unit square? Calculate the determinant of a matrix representing a pure dilation of k.
Answer:
The dilation changes all areas by k2. The pure dilation matrix is \(\), which has a determinant of k2.
c. Does a rotation with no dilation change the area of the unit square? Confirm your answer by calculating the determinant of a pure rotation matrix, and explain it.
Answer:
A pure rotation does not change the area. The pure rotation matrix is \(\). Its determinant is (cos(θ))2-(-sin(θ))2=cos2 (θ)+sin2 (θ)=1, which confirms that the area does not change.
Eureka Math Precalculus Module 1 Lesson 26 Problem Set Answer Key
Question 1.
Perform the following transformation on the unit square: Sketch and state the area of the image.
a. \(\left[\begin{array}{cc}
3 & -1 \\
1 & 3
\end{array}\right]\)
Answer:
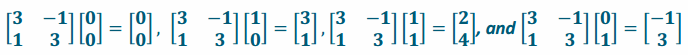
Area=a2+b2=32+12=10
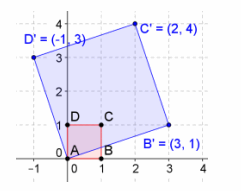
The area is 10 units2.
b. \(\left[\begin{array}{cc}
1 & -3 \\
3 & 1
\end{array}\right]\)
Answer:
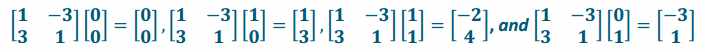
Area=a2+b2=12+32=10
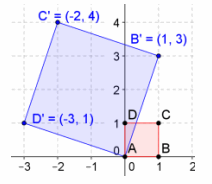
The area is 10 units2.
c. \(\left[\begin{array}{cc}
4 & -2 \\
2 & 4
\end{array}\right]\)
Answer:
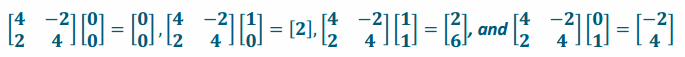
Area=a2+b2=42+22=20
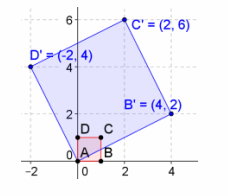
The area is 20 units2.
d. \(\left[\begin{array}{cc}
2 & -4 \\
4 & 2
\end{array}\right]\)
Answer:
![]()
Area=a2+b2=22+42=20
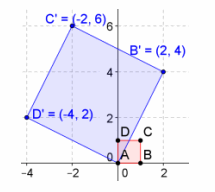
The area is 20 units2.
Question 2.
Perform the following transformation on the unit square: Sketch the image, find the determinant of the given matrix, and find the area of the image.
a. \(\left[\begin{array}{ll}
1 & 3 \\
2 & 4
\end{array}\right]\)
Answer:
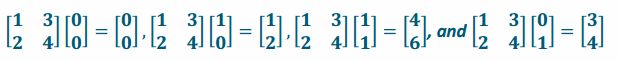
Determinant: ad-bc=4-6=-2 Area=|ad-bc|=|4-6|=2
The area is 2 units2.
b. \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
Answer:
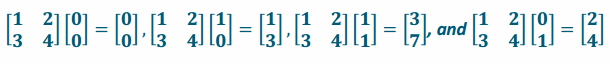
Determinant: ad-bc=4-6=-2 Area=|ad-bc|=|4-6|=2
The area is 2 units2.
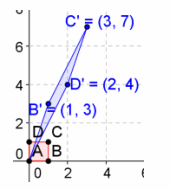
c. \(\left[\begin{array}{ll}
3 & 1 \\
2 & 4
\end{array}\right]\)
Answer:
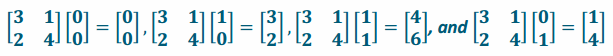
Determinant: ad-bc=12-2=10 Area=|ad-bc|=|12-2|=10
The area is 10 units2.
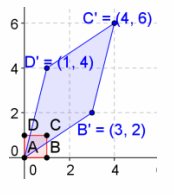
d. \(\left[\begin{array}{ll}
4 & 2 \\
3 & 1
\end{array}\right]\)
Answer:
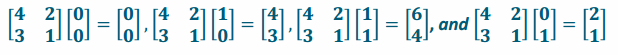
Determinant: ad-bc=4-6=-2 Area=|ad-bc|=|4-6|=2
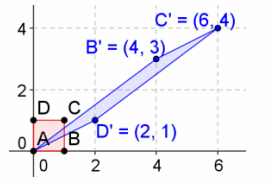
The area is 2 units2.
e. The determinants in parts (a), (b), (c), and (d) have positive or negative values. What is the value of the determinants if the vertices (b, c) and (c, d) are switched?
Answer:
The value is negative.
Question 3.
Perform the following transformation on the unit square: Sketch the image, find the determinant of the given matrix, and find the area of the image.
a. \(\left[\begin{array}{ll}
-1 & -3 \\
-2 & -4
\end{array}\right]\)
Answer:

The area is 2 units2.
b. \(\left[\begin{array}{cc}
-1 & -3 \\
2 & 4
\end{array}\right]\)
Answer:

The area is 2 units2.
c. \(\left[\begin{array}{cc}
1 & 3 \\
-2 & -4
\end{array}\right]\)
Answer:

The area is 2 units2.
d. \(\left[\begin{array}{ll}
-1 & 3 \\
-2 & 4
\end{array}\right]\)
Answer:

The area is 2 units2.
e. \(\left[\begin{array}{ll}
1 & -3 \\
2 & -4
\end{array}\right]\)
Answer:

The area is 2 units2.
f. \(\left[\begin{array}{cc}
-1 & 3 \\
2 & -4
\end{array}\right]\)
Answer:

The area is 2 units2.
g. \(\left[\begin{array}{cc}
1 & -3 \\
-2 & 4
\end{array}\right]\)
Answer:

The area is 2 units2.
Eureka Math Precalculus Module 1 Lesson 26 Exit Ticket Answer Key
Perform the transformation \(\left[\begin{array}{cc}
-2 & 5 \\
4 & -1
\end{array}\right]\) on the unit square.
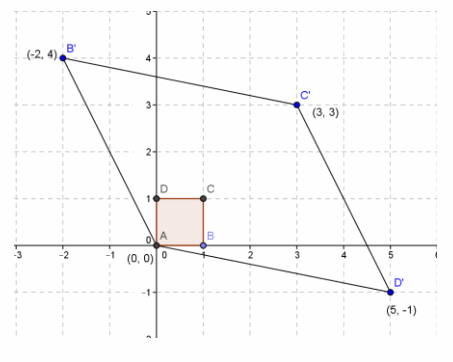
a. Draw the unit square and the image after this transformation.
b. Label the vertices. Explain the effect of this transformation on the unit square.
Answer:
B(1,0)→B'(-2,4)
D(0,1)→D'(5,-1)
C(1,1)→C'(3,3)
A(0,0)→A(0,0)
c. Calculate the area of the image. Show your work.
Answer:
|(-2)(-1)-(5)(4)|=|2-20|=|-18|=18