Download Go Math Grade 4 Answer Key Chapter 8 Multiply Fractions by Whole Numbers pdf for free of cost. Check out the 4th Grade HMH Go Math chapter 8 questions during your preparation and know the topics clearly. Solving the Chapter Test, Practice Test covered questions will help students to score more marks in the exams. Also, they can match the answers with the help of the Go Math Grade 4 Answer Key Chapter 8. Grade 4 Go Math Answer Key Chapter 8 Multiply Fractions by Whole Numbers provided Step by Step Solutions helps you to master the concepts and become a pro in the subject.
Go Math Grade 4 Chapter 8 Multiply Fractions by Whole Numbers Answer Key
The topics of Chapter 8 Multiply Fractions by Whole Numbers having different kinds of methods to solve the questions in no time. Concepts and their step-wise answers are provided in our HMH Go Math Grade 4 Ch 8 Answer Key. So, 4th Grade ch 8 will be easy to solve for those students who practice the sums from Go Math Grade 4 Solutions Key Ch 8 Multiply Fractions by Whole Number.
Lesson 1: Multiples of Unit Fractions
Lesson 2: Multiples of Fractions
- Multiples of Fractions – Page No. 463
- Multiples of Fractions Lesson Check – Page No. 464
- Multiples of Fractions Lesson Check 1 – Page No. 465
- Multiples of Fractions Lesson Check 2 – Page No. 466
Mid-Chapter Checkpoint
Lesson 3: Multiply a Fraction by a Whole Number Using Models
- Multiply a Fraction by a Whole Number Using Models – Page No. 471
- Multiply a Fraction by a Whole Number Using Models Lesson Check – Page No. 472
- Multiply a Fraction by a Whole Number Using Models Lesson Check 1 – Page No. 473
- Multiply a Fraction by a Whole Number Using Models Lesson Check 2 – Page No. 474
Lesson 4: Multiply a Fraction or Mixed Number by a Whole Number
- Multiply a Fraction or Mixed Number by a Whole Number – Page No. 477
- Multiply a Fraction or Mixed Number by a Whole Number Lesson Check – Page No. 478
- Multiply a Fraction or Mixed Number by a Whole Number Lesson Check 1 – Page No. 479
- Multiply a Fraction or Mixed Number by a Whole Number Lesson Check 2- Page No. 480
Lesson 5: Problem Solving • Comparison Problems with Fractions
- Comparison Problems with Fractions – Page No. 483
- Comparison Problems with Fractions Lesson Check – Page No. 484
- Comparison Problems with Fractions Lesson Check 1 – Page No. 485
- Comparison Problems with Fractions Lesson Check 2 – Page No. 486
Review/Test
Common Core – New – Page No. 459
Multiples of Unit Fractions
Write the fraction as a product of a whole number and a unit fraction.
Question 1.

Answer:
5 x 1/6
Explanation:
Given that 5/6 or 5 sixth-size parts.
Each sixth-size part of the given fraction can be shown by the unit fraction 1/6.
You can use unit fractions to show 5/6
5/6 = 5 x 1/6.
Question 2.
\(\frac{7}{8}\) =
Type below:
__________
Answer:
7 x 1/8
Explanation:
Given that 7/8 or 7 eighth-size parts.
Each eighth-size part of the given fraction can be shown by the unit fraction 1/8.
You can use unit fractions to show 7/8
7/8 = 7 x 1/8.
Question 3.
\(\frac{5}{3}\) =
Type below:
__________
Answer:
5 x 1/3
Explanation:
Given that 5/3 or 5 third-size parts.
Each third-size part of the given fraction can be shown by the unit fraction 1/3.
You can use unit fractions to show 5/6
5/3 = 5 x 1/3.
Question 4.
\(\frac{9}{10}\) =
Type below:
__________
Answer:
9 x 1/10
Explanation:
Given that 9/10 or 9 tenth-size parts.
Each tenth-size part of the given fraction can be shown by the unit fraction 1/10.
You can use unit fractions to show 9/10
9/10 = 9 x 1/10.



Question 8.
\(\frac{8}{20}\) =
Type below:
__________
Answer:
8 x 1/20
Explanation:
Given that 8/20 or 8 twenty-size parts.
Each twenty-size part of the given fraction can be shown by the unit fraction 1/20.
You can use unit fractions to show 8/20
8/20 = 8 x 1/20.
Question 9.
\(\frac{13}{100}\) =
Type below:
__________
Answer:
13 x 1/100
Explanation:
Given that 13/100 or 13 hundred-size parts.
Each hundred-size part of the given fraction can be shown by the unit fraction 1/100.
You can use unit fractions to show 13/100
13/100 = 13 x 1/100.
List the next four multiples of the unit fraction.
Question 10.
\(\frac{1}{5}\) ,
Type below:
__________
Answer:
2/5, 3/5, 4/5, 5/5
Explanation:
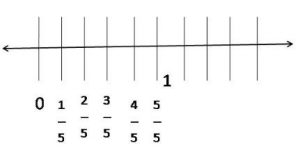
2/5, 3/5, 4/5, 5/5
Question 11.
\(\frac{1}{8}\) ,
Type below:
__________
Answer:
2/8, 3/8, 4/8, 5/8
Explanation:
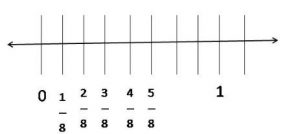
2/8, 3/8, 4/8, 5/8
Problem Solving
Question 12.
So far, Monica has read \(\frac{5}{6}\) of a book. She has read the same number of pages each day for 5 days. What fraction of the book does Monica read each day?
\(\frac{□}{□}\) of the book
Answer:
1/6 of the book
Explanation:
Monica has read 5/6 of a book. She has read the same number of pages each day for 5 days.
For 1 day, she read one page. In total, she read 5 pages in 5 days. So, Monica read 1/6 of a book each day.
Question 13.
Nicholas buys \(\frac{3}{8}\) pound of cheese. He puts the same amount of cheese on 3 sandwiches. How much cheese does Nicholas put on each sandwich?
\(\frac{□}{□}\) pound of cheese
Answer:
1/8 pound of cheese
Explanation:
Nicholas buys 3/8 pound of cheese. He bought 3 sandwiches. Then, he applied 3/8 pound of cheese on 3 sandwiches. So, 3 x 1/8 cheese he put on 3 sandwiches. So, for one sandwich he put 1/8 pound of cheese.
Common Core – New – Page No. 460
Lesson Check
Question 1.
Selena walks from home to school each morning and back home each afternoon. Altogether, she walks \(\frac{2}{3}\) mile each day. How far does Selena live from school?
Options:
a. \(\frac{1}{3}\) mile
b. \(\frac{2}{3}\) mile
c. 1 \(\frac{1}{3}\) mile
d. 2 miles
Answer:
a. \(\frac{1}{3}\) mile
Explanation:
Selena walks from home to school each morning and back home each afternoon. Altogether, she walks 2/3 miles each day. The distance between home and school will remain the same. So, 2/3 x 1/2 = 1/3 mile far Selena live from the school.
Question 2.
Will uses \(\frac{3}{4}\) cup of olive oil to make 3 batches of salad dressing. How much oil does Will use for one batch of salad dressing?
Options:
a. \(\frac{1}{4}\) cup
b. \(\frac{1}{3}\) cup
c. 2 \(\frac{1}{3}\) cups
d. 3 cups
Answer:
1/8 pound of cheesa. \(\frac{1}{4}\) cup
Explanation:
Will uses 34 cups of olive oil to make 3 batches of salad dressing. To know the one batch of salad dressing, we need to take one part of salad dressing = 1/3. So, 3/4 x 1/3 = 1/4 cup of olive oil will use for one batch of salad dressing.
Spiral Review
Question 3.
Liza bought \(\frac{5}{8}\) pound of trail mix. She gives \(\frac{2}{8}\) pound of trail mix to Michael. How much trail mix does Liza have left?
Options:
a. \(\frac{1}{8}\) pound
b. \(\frac{2}{8}\) pound
c. \(\frac{3}{8}\) pound
d. \(\frac{4}{8}\) pound
Answer:
c. \(\frac{3}{8}\) pound
Explanation:
Liza bought 58 pound of trail mix. She gives 28 pound of trail mix to Michael.
So, Liza have left 5/8 – 2/8 = 3/8 trail mix.
Question 4.
Leigh has a piece of rope that is 6 \(\frac{2}{3}\) feet long. How do you write 6 \(\frac{2}{3}\) as a fraction greater than 1?
Options:
a. \(\frac{11}{3}\)
b. \(\frac{15}{3}\)
c. \(\frac{20}{3}\)
d. \(\frac{62}{3}\)
Answer:
c. \(\frac{20}{3}\)
Explanation:
Multiply the denominator with the whole number. i.e Multiply 3 with 6 in the given example, 6 (2/3).
3 x 6 =18.
Add 18 + 2 =20.
Keep the Denominator the same i.e. 3.
The obtained fraction is 20/3.
Question 5.
Randy’s house number is a composite number. Which of the following could be Randy’s house number?
Options:
a. 29
b. 39
c. 59
d. 79
Answer:
b. 39
Explanation:
The composite numbers can be defined as the whole numbers that have more than two factors. Whole numbers that are not prime are composite numbers because they are divisible by more than two numbers. 39 is the composite number. 39 is divide by 13 and 3.
Question 6.
Mindy buys 12 cupcakes. Nine of the cupcakes have chocolate frosting and the rest have vanilla frosting. What fraction of the cupcakes have vanilla frosting?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{1}{3}\)
c. \(\frac{2}{3}\)
d. \(\frac{3}{4}\)
Answer:
a. \(\frac{1}{4}\)
Explanation:
Mindy buys 12 cupcakes.
Nine of the cupcakes have chocolate frosting = 9/12.
The rest have vanilla frosting. So, there are 3 cups remained = 3/12 = 1/4.
1/4 cupcakes have vanilla frosting.
Page No. 463
Question 1.
Write three multiples of \(\frac{3}{8}\).
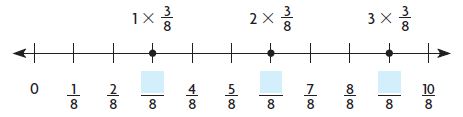
1 × \(\frac{3}{8}\) = \(\frac{■}{8}\)
2 × \(\frac{3}{8}\) = \(\frac{■}{8}\)
3 × \(\frac{3}{8}\) = \(\frac{■}{8}\)
Multiples of \(\frac{3}{8}\) are ____ , ____ , and ____ .
Type below:
__________
Answer:
3/8, 6/8, 9/8, 12/8.
Explanation:
1 x 3/8 = 3/8.
2 x 3/8 = 6/8.
3 x 3/8 = 9/8.
4 x 3/8 = 12/8.
Multiples of 3/8 are 3/8, 6/8, 9/8, 12/8.
List the next four multiples of the fraction.

Write the product as the product of a whole number and a unit fraction.
Question 4.
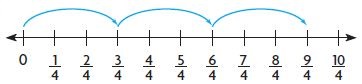
3 × \(\frac{3}{4}\) =
Type below:
__________
Answer:
9/4 = 9 x 1/4
Explanation:
1 group of 3/4 = 3/4
2 groups of 3/4 = 6/4
3 groups of 3/4 = 9/4
3 x 3/4 = 9/4.
Question 5.
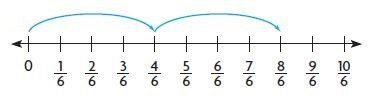
2 × \(\frac{4}{6}\) =
Type below:
__________
Answer:
8/6 = 8 x 1/6
Explanation:
1 group of 4/6 = 4/6
2 groups of 4/6 = 8/6
2 x 4/6 = 8/6 = 8 x 1/6.
List the next four multiples of the fraction.
Question 6.
\(\frac{4}{5}\) ,
Type below:
__________
Answer:
8/5, 12/5, 16/5, 20/5
Explanation:
1 x 4/5 = 4/5.
2 x 4/5 = 8/5.
3 x 4/5 = 12/5.
4 x 4/5 = 16/5.
5 x 4/5 = 20/5.
The next four multiples of 4/5 are 8/5, 12/5, 16/5, 20/5.
Question 7.
\(\frac{2}{4}\) ,
Type below:
__________
Answer:
4/4, 6/4, 8/4, 10/4
Explanation:
1 x 2/4 = 2/4.
2 x 2/4 = 4/4.
3 x 2/4 = 6/4.
4 x 2/4 = 8/4.
5 x 2/4 = 10/4.
The next four multiples of 2/4 are 4/4, 6/4, 8/4, 10/4.
Write the product as the product of a whole number and a unit fraction.
Question 8.
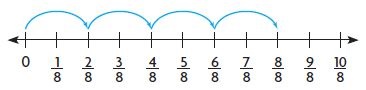
4 × \(\frac{2}{8}\) =
Type below:
__________
Answer:
8/8 = 8 x 1/8
Explanation:
1 group of 2/8 = 2/8
2 groups of 2/8 = 4/8
3 groups of 2/8 = 6/8
4 groups of 2/8 = 8/8
4 x 2/8 = 8/8 = 8 x 1/8.
Question 9.
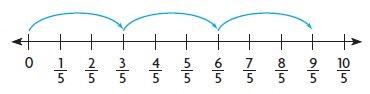
3 × \(\frac{3}{5}\) =
Type below:
__________
Answer:
9/5 = 9 x 1/5
Explanation:
1 group of 3/5 = 3/5
2 groups of 3/5 = 6/5
3 groups of 3/5 = 9/5
3 x 3/5 = 9/5 = 9 x 1/5.


Page No. 464
Question 12.
Josh is watering his plants. He gives each of 2 plants \(\frac{3}{5}\) pint of water. His watering can holds \(\frac{1}{5}\) pint. How many times will he fill his watering can to water both plants?

a. What do you need to find?
Type below:
__________
Answer:
We need to find how many times Josh needs to fill his watering can to water both plants.
Question 12.
b. What information do you need to use?
Type below:
__________
Answer:
Use the Number of plants = 2.
He gives each plant a 3/5 pint of water.
His watering can hold 1/5 pint.
Question 12.
c. How can drawing a model help you solve the problem?
Type below:
__________
Answer:

Question 12.
d. Show the steps you use to solve the problem.
Type below:
__________
Answer:
If Josh gives each plant 3/5 pint, then that’s a total of 6/5 pint.
6/5 = 6 x 1/5.
Question 12.
e. Complete the sentence. Josh will fill his watering can ____ times.
____ times
Answer:
Josh will fill his watering can 6 times.
Question 13.
Alma is making 3 batches of tortillas. She adds \(\frac{3}{4}\) cup of water to each batch. The measuring cup holds \(\frac{1}{4}\) cup. How many times must Alma measure \(\frac{1}{4}\) cup of water to have enough for the tortillas? Shade the model to show your answer.
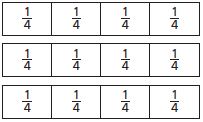
Alma must measure \(\frac{1}{4}\) cup ______ times.
____ times
Answer:
12 times
Explanation:
Alma is making 3 batches of tortillas. She adds a 3/4 cup of water to each batch. The measuring cup holds 1/4 cup.
Alma must measure 1/4 cup 12 times.
Common Core – New – Page No. 465
Multiples of Fractions
List the next four multiples of the fraction.
Question 1.
\(\frac{3}{5}\) ,
Type below:
__________
Answer:
6/5, 9/5, 12/5, 20/5
Explanation:
1 x 3/5 = 3/5.
2 x 3/5 = 6/5.
3 x 3/5 = 9/5.
4 x 3/5 = 12/5.
5 x 4/5 = 20/5.
The next four multiples of 3/5 are 6/5, 9/5, 12/5, 20/5.
Question 2.
\(\frac{2}{6}\) ,
Type below:
__________
Answer:
4/6, 6/6, 8/6, 10/6
Explanation:
1 x 2/6 = 2/6.
2 x 2/6 = 4/6.
3 x 2/6 = 6/6.
4 x 2/6 = 8/6.
5 x 2/6 = 10/6.
The next four multiples of 2/6 are 4/6, 6/6, 8/6, 10/6.
Question 3.
\(\frac{4}{8}\) ,
Type below:
__________
Answer:
8/8, 12/8, 16/8, 20/8
Explanation:
1 x 4/8 = 4/8.
2 x 4/8 = 8/8.
3 x 4/8 = 12/8.
4 x 4/8 = 16/8.
5 x 4/8 = 20/8.
The next four multiples of 4/8 are 8/8, 12/8, 16/8, 20/8.
Question 4.
\(\frac{5}{10}\) ,
Type below:
__________
Answer:
10/10, 15/10, 20/10, 25/10
Explanation:
1 x 5/10 = 5/10.
2 x 5/10 = 10/10.
3 x 5/10 = 15/10.
4 x 5/10 = 20/10.
5 x 5/10 = 25/10.
The next four multiples of 5/10 are 10/10, 15/10, 20/10, 25/10.
Write the product as the product of a whole number and a unit fraction.
Question 5.
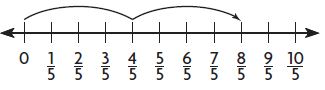
2 × \(\frac{4}{5}\) =
Type below:
__________
Answer:
8/5 = 8 x 1/5
Explanation:
1 group of 4/5 = 4/5
2 groups of 4/5 = 8/5
2 x 4/5 = 8/5 = 8 x 1/5.
Question 6.
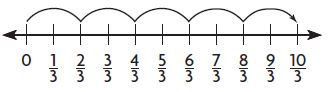
5 × \(\frac{2}{3}\) =
Type below:
__________
Answer:
10/3 = 10 x 1/3
Explanation:
1 group of 2/3 = 2/3
2 group of 2/3 = 4/3
3 group of 2/3 = 6/3
4 group of 2/3 = 8/3
5 group of 2/3 = 10/3
5 x 2/3 = 10/3 = 10 x 1/3.
Problem Solving
Question 7.
Jessica is making 2 loaves of banana bread. She needs \(\frac{3}{4}\) cup of sugar for each loaf. Her measuring cup can only hold \(\frac{1}{4}\) cup of sugar. How many times will Jessica need to fill the measuring cup in order to get enough sugar for both loaves of bread?
_____ times
Answer:
6 times
Explanation:
Jessica is making 2 loaves of banana bread. She needs a 3/4 cup of sugar for each loaf.
For 2 loaves, she needs 2 x 3/4 = 6/4 cups of sugar.
Her measuring cup can only hold 1/4 cup of sugar. So, to get the 3/4 cup of sugar, she needs to fill the cup 3 times. 1/4 + 1/4 + 1/4 = 3/4.
So, to fill 2 loaves, she needs to fill cup 3 x 2 = 6 times.
Question 8.
A group of four students is performing an experiment with salt. Each student must add \(\frac{3}{8}\) teaspoon of salt to a solution. The group only has a \(\frac{1}{8}\) teaspoon measuring spoon. How many times will the group need to fill the measuring spoon in order to perform the experiment?
_____ times
Answer:
12 times
Explanation:
A group of four students is performing an experiment with salt. Each student must add a 3/8 teaspoon of salt to a solution. 4 x 3/8 = 12/8 teaspoon of salt required to finish the experiment.
If they have 1/8 teaspoon measuring spoon, 12 x 1/8.
So, the group needs to fill the measuring spoon 12 times in order to perform the experiment.
Common Core – New – Page No. 466
Lesson Check
Question 1.
Eloise made a list of some multiples of \(\frac{5}{8}\). Which of the following lists could be Eloise’s list?
Options:
a. \(\frac{5}{8}, \frac{10}{16}, \frac{15}{24}, \frac{20}{32}, \frac{25}{40}\)
b. \(\frac{5}{8}, \frac{10}{8}, \frac{15}{8}, \frac{20}{8}, \frac{25}{8}\)
c. \(\frac{5}{8}, \frac{6}{8}, \frac{7}{8}, \frac{8}{8}, \frac{9}{8}\)
d. \(\frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8}, \frac{5}{8}\)
Answer:
b. \(\frac{5}{8}, \frac{10}{8}, \frac{15}{8}, \frac{20}{8}, \frac{25}{8}\)
Explanation:
1 x 5/8 = 5/8.
2 x 5/8 = 10/8.
3 x 5/8 = 15/8.
4 x 5/8 = 20/8.
5 x 5/8 = 25/8.
The next four multiples of 5/8 are 10/8, 15/8, 20/8, 25/8.
Question 2.
David is filling five \(\frac{3}{4}\) quart bottles with a sports drink. His measuring cup only holds \(\frac{1}{4}\) quart. How many times will David need to fill the measuring cup in order to fill the 5 bottles?
Options:
a. 5
b. 10
c. 15
d. 20
Answer:
c. 15
Explanation:
David is filling five 3/4 quart bottles with a sports drink = 5 x 3/4 = 15/4.
His measuring cup only holds 1/4 quart.
So, 15 x 1/4. David needs to fill the measuring cup 15 times in order to fill the 5 bottles.
Spiral Review
Question 3.
Ira has 128 stamps in his stamp album. He has the same number of stamps on each of the 8 pages. How many stamps are on each page?
Options:
a. 12
b. 14
c. 16
d. 18
Answer:
c. 16
Explanation:
Ira has 128 stamps in his stamp album. He has the same number of stamps on each of the 8 pages.
128/8 = 16 stamps on each page.
Question 4.
Ryan is saving up for a bike that costs $198. So far, he has saved $15 per week for the last 12 weeks. How much more money does Ryan need in order to be able to buy the bike?
Options:
a. $ 8
b. $ 18
c. $ 48
d. $ 180
Answer:
b. $ 18
Explanation:
Ryan is saving up for a bike that costs $198.
So far, he has saved $15 per week for the last 12 weeks = $15 x 12 = $180.
$198 – $180 = $18 need in order to buy the bike.
Question 5.
Tina buys 3 \(\frac{7}{8}\) yards of material at the fabric store. She uses it to make a skirt. Afterward, she has 1 \(\frac{3}{8}\) yards of the fabric leftover. How many yards of material did Tina use?
Options:
a. 1 \(\frac{4}{8}\)
b. 2 \(\frac{1}{8}\)
c. 2 \(\frac{4}{8}\)
d. 5 \(\frac{2}{8}\)
Answer:
c. 2 \(\frac{4}{8}\)
Explanation:
Tina buys 3 7/8 yards of material at the fabric store. She uses it to make a skirt. Afterward, she has 1 3/8 yards of the fabric leftover.
3 -1 = 2; 7/8 – 3/8 = 4/8. So, answer is 2 4/8.
Question 6.
Which list shows the fractions in order from least to greatest?
Options:
a. \(\frac{2}{3}, \frac{3}{4}, \frac{7}{12}\)
b. \(\frac{7}{12}, \frac{3}{4}, \frac{2}{3}\)
c. \(\frac{3}{4}, \frac{2}{3}, \frac{7}{12}\)
d. \(\frac{7}{12}, \frac{2}{3}, \frac{3}{4}\)
Answer:
d. \(\frac{7}{12}, \frac{2}{3}, \frac{3}{4}\)
Explanation:
2/3 = 0.666
3/4 = 0.75
7/12 = 0.5833
7/12, 2/3, 3/4
Page No. 467
Choose the best term from the box.
Question 1.
A __________ of a number is the product of the number and a counting number.
__________
Answer:
Multiple
Question 2.
A _________ always has a numerator of 1.
_________
Answer:
Unit Fraction
List the next four multiples of the unit fraction.


Write the fraction as a product of a whole number and a unit fraction.
Question 5.
\(\frac{4}{10}\) = _____ × \(\frac{1}{10}\)
Answer:
4
Explanation:
4/10 = 4 x 1/10
Question 6.
\(\frac{8}{12}\) = _____ × \(\frac{1}{12}\)
Answer:
8
Explanation:
8/12 = 8 x 1/12
Question 7.
\(\frac{3}{4}\) = _____ × \(\frac{1}{4}\)
Answer:
3
Explanation:
3/4 = 3 x 1/4
List the next four multiples of the fraction.
Question 8.
\(\frac{2}{5}\) ,
Type below:
_________
Answer:
4/5, 6/5, 8/5, 10/5
Explanation:
1 x 2/5 = 1/5.
2 x 2/5 = 4/5.
3 x 2/5 = 6/5.
4 x 2/5 = 8/5.
5 x 2/5 = 10/5.
The next four multiples of 1/5 are 4/5, 6/5, 8/5, 10/5.
Question 9.
\(\frac{5}{6}\) ,
Type below:
_________
Answer:
10/6, 15/6, 20/6, 25/6
Explanation:
1 x 5/6 = 5/6.
2 x 5/6 = 10/6.
3 x 5/6 = 15/6.
4 x 5/6 = 20/6.
5 x 5/6 = 25/6.
The next four multiples of 5/6 are 10/6, 15/6, 20/6, 25/6.
Write the product as the product of a whole number and a unit fraction.
Question 10.
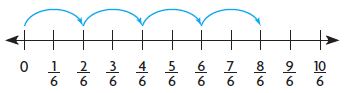
4 × \(\frac{2}{6}\) =
Type below:
_________
Answer:
8/6 = 8 x 1/6
Explanation:
1 group of 2/6 = 2/6
2 groups of 2/6 = 4/6
3 groups of 2/6 = 6/6
4 groups of 2/6 = 8/6
4 x 2/6 = 8/6 = 8 x 1/6.
Question 11.
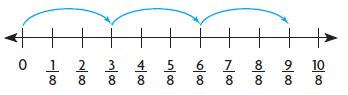
3 × \(\frac{3}{8}\) =
Type below:
_________
Answer:
9/8 = 9 x 1/8
Explanation:
1 group of 3/8 = 3/8
2 groups of 3/8 = 6/8
3 groups of 3/8 = 9/8
3 x 3/8 = 9/8 = 9 x 1/8.
Page No. 468
Question 12.
Pedro cut a sheet of poster board into 10 equal parts. His brother used some of the poster board and now \(\frac{8}{10}\) is left. Pedro wants to make a sign from each remaining part of the poster board. How many signs can he make?
______ signs
Answer:
8 signs
Explanation:
Pedro cut a sheet of poster board into 10 equal parts.
His brother uses some of the poster board and now an 8/10 is left.
So, the remaining part of the b\poster board is 8/10 parts.
Pedro can use 8/ 10 parts of the board to make signs.
So, he can make 8 signs.
Question 13.
Ella is making 3 batches of banana milkshakes. She needs \(\frac{3}{4}\) gallon of milk for each batch. Her measuring cup holds \(\frac{1}{4}\) gallon. How many times will she need to fill the measuring cup to make all 3 batches of milkshakes?
______ times
Answer:
9 times
Explanation:
Ella is making 3 batches of banana milkshakes. She needs 3/4 gallon of milk for each batch. So, she needs 3 x 3/4 = 9/4 cups for 3 batches of banana milkshakes. Her measuring cup holds 1/4 gallon.
9/4 = 9 x 1/4.
So, Ella needs to fill the measuring cup 9 times to make all 3 batches of milkshakes.
Question 14.
Darren cut a lemon pie into 8 equal slices. His friends ate some of the pie and now \(\frac{5}{8}\) is left. Darren wants to put each slice of the leftover pie on its own plate. What part of the pie will he put on each plate?
\(\frac{□}{□}\) of the pie on each plate.
Answer:
5/8 of the pie on each plate
Explanation:
Darren cut a lemon pie into 8 equal slices. His friends ate some of the pie and now 5/8 is left. So, 5 pie slices leftover.
Darren can put 5/8 parts of the pie on each plate.
Question 15.
Beth is putting liquid fertilizer on the plants in 4 flowerpots. Her measuring spoon holds \(\frac{1}{8}\) teaspoon. The directions say to put \(\frac{5}{8}\) teaspoon of fertilizer in each pot. How many times will Beth need to fill the measuring spoon to fertilize the plants in the 4 pots?
______ times
Answer:
20 times
Explanation:
Beth is putting liquid fertilizer on the plants in 4 flowerpots. Her measuring spoon holds 1/8 teaspoon.
The directions say to put 5/8 teaspoons of fertilizer in each pot. So, 4 x 5/8 = 20/8.
20/8 = 20 x 1/8. Beth needs to fill the measuring spoon 20 times to fertilize the plants in the 4 pots.
Page No. 471
Question 1.
Find the product of 3 × \(\frac{5}{8}\).
1 group of \(\frac{5}{8}\) = \(\frac{□}{8}\)
2 groups of \(\frac{5}{8}\) = \(\frac{□}{8}\)
3 groups of \(\frac{5}{8}\) = \(\frac{□}{8}\)
3 × \(\frac{5}{8}\) = \(\frac{□}{□}\)
Answer:
15/8
Explanation:
1 group of 5/8 = 2/8
2 groups of 5/8 = 4/8
3 groups of 5/8 = 6/8
3 x 5/8 = 15/8.
Multiply.
Question 2.
2 × \(\frac{4}{5}\) = \(\frac{□}{□}\)
Answer:
8/5
Explanation:
1 group of 4/5 = 4/5
2 groups of 4/5 = 8/5
2 x 4/5 = 8/5.
Question 3.
4 × \(\frac{2}{3}\) = \(\frac{□}{□}\)
Answer:
8/3
Explanation:
1 group of 2/3 = 2/3
2 groups of 2/3 = 4/3
3 groups of 2/3 = 6/3
4 groups of 2/3 = 8/3
4 x 2/3 = 8/3
Question 4.
5 × \(\frac{3}{10}\) = \(\frac{□}{□}\)
Answer:
15/10
Explanation:
1 group of 3/10 = 3/10
2 groups of 3/10 = 6/10
3 groups of 3/10 = 9/10
4 groups of 3/10 = 12/10
5 groups of 3/10 = 15/10
5 x 3/10 = 15/10
Question 5.
4 × \(\frac{5}{6}\) = \(\frac{□}{□}\)
Answer:
20/6
Explanation:
1 group of 5/6 = 5/6
2 groups of 5/6 = 10/6
3 groups of 5/6 = 15/6
4 groups of 5/6 = 20/6
4 x 5/6 = 20/6
Multiply.


Question 8.
5 × \(\frac{2}{4}\) = \(\frac{□}{□}\)
Answer:
5/2
Explanation:
1 group of 2/4 = 2/4
2 groups of 2/4 = 4/4
3 groups of 2/4 = 6/4
4 groups of 2/4 = 8/4
5 groups of 2/4 = 10/4
5 x 2/4 = 10/4 = 5/2
Question 9.
3 × \(\frac{4}{6}\) = \(\frac{□}{□}\)
Answer:
2
Explanation:
1 group of 4/6 = 4/6
2 groups of 4/6 = 8/6
3 groups of 4/6 = 12/6
3 x 4/6 = 12/6 = 2
Question 10.
2 × \(\frac{5}{10}\) = \(\frac{□}{□}\)
Answer:
2
Explanation:
1 group of 5/10 = 5/10
2 groups of 5/10 = 10/10
2 x 10/10 = 2 x 1 = 2
Question 11.
4 × \(\frac{2}{8}\) = \(\frac{□}{□}\)
Answer:
1
Explanation:
1 group of 2/8 = 2/8
2 groups of 2/8 = 4/8
3 groups of 2/8 = 6/8
4 groups of 2/8 = 8/8
4 x 2/8 = 8/8 = 1
Look for a Pattern Algebra Write the unknown number.

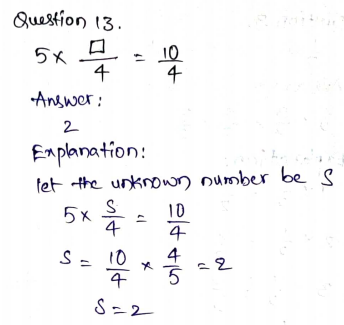
Question 14.
2 × \(\frac{7}{□}\) = \(\frac{14}{8}\)
□ = ____
Answer:
8
Explanation:
Let the unknown number is s.
2 x 7/s = 14/8
14/s = 14/8
s x 14/8 = 14
s = 14 x 8/14
s = 8.
Page No. 472
Question 15.
Lisa makes clothes for pets. She needs \(\frac{5}{6}\) yard of fabric to make 1 dog coat. How much fabric does she need to make 3 dog coats?
a. What do you need to find?
Type below:
_________
Answer:
The number of fabric yards required for 3 dog coats
Question 15.
b. What information do you need?
Type below:
_________
Answer:
How much she needs of fabric for 1 dog coat can helps to find for 3 dog coats.
Question 15.
c. Show the steps you use to solve the problem.
Type below:
_________
Answer:
Lisa makes clothes for pets. She needs a 5/6 yard of fabric to make 1 dog coat.
For 3 dogs = 5/6 x 3 =5/2
Question 15.
d. Complete the sentence.
Lisa needs _____ yards of fabric to make 3 dog coats.
\(\frac{□}{□}\)
Answer:
Lisa needs a 5/2 yard of fabric to make 3 dog coats.

Question 17.
Select the correct product for the equation.
9 × \(\frac{2}{12}\) = □
3 × \(\frac{6}{7}\) = □
6 × \(\frac{4}{7}\) = □
8 × \(\frac{3}{12}\) = □
Type below:
_________
Answer:
8 × \(\frac{3}{12}\) = 2
Explanation:
9 × \(\frac{2}{12}\) = 3/2
3 × \(\frac{6}{7}\) = 18/7
6 × \(\frac{4}{7}\) = 24/7
8 × \(\frac{3}{12}\) = 2
Common Core – New – Page No. 473
Multiply a Fraction by a Whole Number Using Models
Multiply.
Question 1.
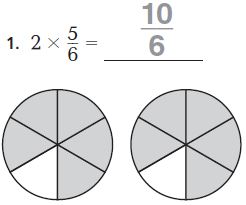
Answer:

Question 2.
3 × \(\frac{2}{5}\) = \(\frac{□}{□}\)
Answer:
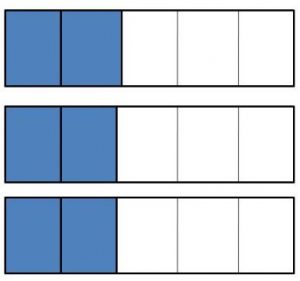
3 x 2/5 = 6/5
Question 3.
7 × \(\frac{3}{10}\) = \(\frac{□}{□}\)
Answer:
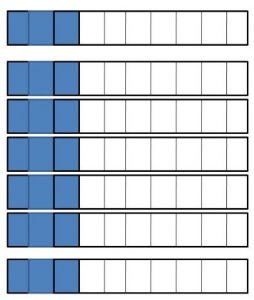
7 x 3/10 = 21/10
Question 4.
3 × \(\frac{5}{12}\) = \(\frac{□}{□}\)
Answer:
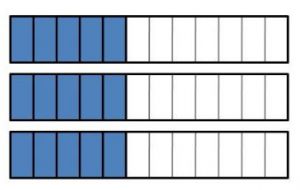
3 x 5/12 = 15/12
Question 5.
6 × \(\frac{3}{4}\) = \(\frac{□}{□}\)
Answer:
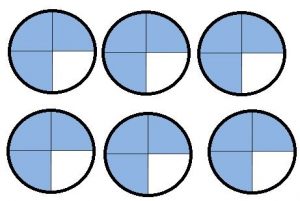
6 x 3/4 = 18/4
Question 6.
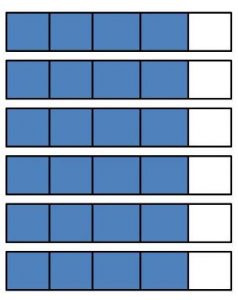
4 × \(\frac{2}{8}\) = \(\frac{□}{□}\)
Answer:
4 x 2/8 = 8/8
Question 7.
5 × \(\frac{2}{3}\) = \(\frac{□}{□}\)
Answer:
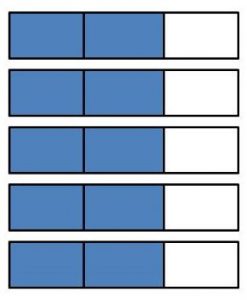
5 x 2/3 = 10/3
Question 8.
2 × \(\frac{7}{8}\) = \(\frac{□}{□}\)
Answer:
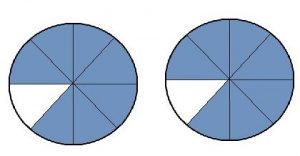
2 x 7/8 = 14/8
Question 9.
6 × \(\frac{4}{5}\) = \(\frac{□}{□}\)
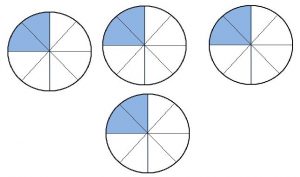
Answer:
6 x 4/5 = 28/5
Problem Solving

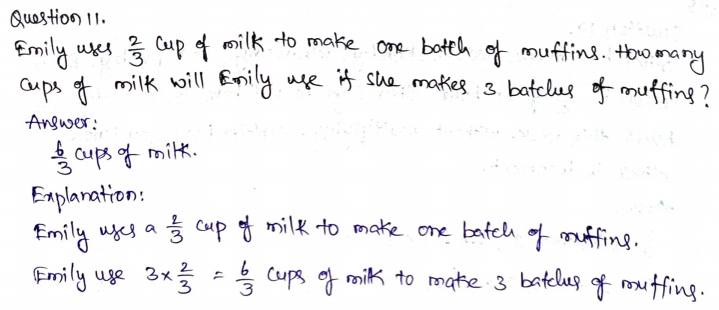
Common Core – New – Page No. 474
Lesson Check
Question 1.
Aleta’s puppy gained \(\frac{3}{8}\) pound each week for 4 weeks. Altogether, how much weight did the puppy gain during the 4 weeks?
Options:
a. \(\frac{8}{12}\) pound
b. 1 \(\frac{2}{8}\) pounds
c. \(\frac{12}{8}\) pounds
d. 4 \(\frac{3}{8}\) pounds
Answer:
6/3 cups of milk
Explanation:
Aleta’s puppy gained 3/8 pound each week.
It gained 4 x 3/8 = 12/8 pounds in 4 weeks.
Question 2.
Pedro mixes \(\frac{3}{4}\) teaspoon of plant food into each gallon of water. How many teaspoons of plant food should Pedro mix into 5 gallons of water?
Options:
a. \(\frac{3}{20}\) teaspoon
b. \(\frac{4}{15}\) teaspoon
c. \(\frac{8}{4}\) teaspoons
d. \(\frac{15}{4}\) teaspoons
Answer:
d. \(\frac{15}{4}\) teaspoons
Explanation:
If Pedro mixes 3/4 teaspoon of plant food into each gallon of water, then 5 x 3/4 = 15/4 teaspoon of plant food mix into 5 gallons of water.
Spiral Review
Question 3.
Ivana has \(\frac{3}{4}\) pound of hamburger meat. She makes 3 hamburger patties. Each patty weighs the same amount. How much does each hamburger patty weigh?
Options:
a. \(\frac{1}{4}\) pound
b. \(\frac{1}{3}\) pound
c. 2 \(\frac{1}{4}\) pounds
d. 3 pounds
Answer:
a. \(\frac{1}{4}\) pound
Explanation:
Ivana has 3/4 pound of hamburger meat. She makes 3 hamburger patties.
Each patty weighs the same amount. So, each hamburger patty weight 1/4 pound.
Question 4.
Which of the following expressions is NOT equal to \(\frac{7}{10}\)?
Options:
a. \(\frac{5}{10}+\frac{1}{10}+\frac{1}{10}\)
b. \(\frac{2}{10}+\frac{2}{10}+\frac{3}{10}\)
c. \(\frac{3}{10}+\frac{3}{10}+\frac{2}{10}\)
d. \(\frac{4}{10}+\frac{2}{10}+\frac{1}{10}\)
Answer:
c. \(\frac{3}{10}+\frac{3}{10}+\frac{2}{10}\)
Explanation:
a. \(\frac{5}{10}+\frac{1}{10}+\frac{1}{10}\) = 7/10
b. \(\frac{2}{10}+\frac{2}{10}+\frac{3}{10}\) = 7/10
c. \(\frac{3}{10}+\frac{3}{10}+\frac{2}{10}\) = 8/10
d. \(\frac{4}{10}+\frac{2}{10}+\frac{1}{10}\) = 7/10
Question 5.
Lance wants to find the total length of 3 boards. He uses the expression 3 \(\frac{1}{2}\) + (2 + 4 \(\frac{1}{2}\)). How can Lance rewrite the expression using both the Associative and Commutative Properties of Addition?
Options:
a. 5 + 4 \(\frac{1}{2}\)
b. (3 \(\frac{1}{2}\) + 2) + 4 \(\frac{1}{2}\)
c. 2 + (3 \(\frac{1}{2}\) + 4 \(\frac{1}{2}\))
d. 3 \(\frac{1}{2}\) + (4 \(\frac{1}{2}\) + 2)
Answer:
She can write as (3 \(\frac{1}{2}\) + 2) + 4 \(\frac{1}{2}\)
Question 6.
Which of the following statements is true?
Options:
a. \(\frac{5}{8}>\frac{9}{10}\)
b. \(\frac{5}{12}>\frac{1}{3}\)
c. \(\frac{3}{6}>\frac{4}{5}\)
d. \(\frac{1}{2}>\frac{3}{4}\)
Answer:
6/3 cups of milk
Explanation:
0.625 > 0.9
0.416 > 0.333
0.5 > 0.8
0.5 > 0.75
Page No. 477
Question 1.
2 × 3 \(\frac{2}{3}\) = □
_____ \(\frac{□}{□}\)
Answer:
7\(\frac{1}{3}\)
Explanation:
3 \(\frac{2}{3}\) = 11/3
2 x 11/3 = 22/3
22/3 = 7 and remainder 1. So, 22/3 = 7 (1/3)
Multiply. Write the product as a mixed number.


Question 4.
4 × 1 \(\frac{5}{6}\) = _____ \(\frac{□}{□}\)
Answer:
7 \(\frac{2}{6}\)
Explanation:
1 \(\frac{5}{6}\) = 11/6
4 x 11/6 = 44/6. 44/6 = 7 and remainder 2. So, 44/6 = 7 2/6
Question 5.
4 × \(\frac{5}{8}\) = _____ \(\frac{□}{□}\)
Answer:
2\(\frac{1}{2}\)
Explanation:
4 × \(\frac{5}{8}\) = 5/2. 5/2 = 2 and remainder 1. So, 5/2 = 2 1/2
Question 6.
6 × \(\frac{5}{12}\) = _____ \(\frac{□}{□}\)
Answer:
2\(\frac{1}{2}\)
Explanation:
6 × \(\frac{5}{12}\) = 5/2. 5/2 = 2 and remainder 1. So, 5/2 = 2 1/2
Question 7.
3 × 3 \(\frac{1}{2}\) = _____ \(\frac{□}{□}\)
Answer:
10 \(\frac{1}{2}\)
Explanation:
3 \(\frac{1}{2}\) = 7/2
3 x 7/2 = 21/2. 21/2 = 10 and remainder 1. So, 21/2 = 10 1/2
Question 8.
2 × 2 \(\frac{2}{3}\) = _____ \(\frac{□}{□}\)
Answer:
5\(\frac{1}{3}\)
Explanation:
2 \(\frac{2}{3}\) = 8/3
2 x 8/3 = 16/3. 16/3 = 5 and remainder 1. So, 16/3 = 5 1/3
Question 9.
5 × 1 \(\frac{2}{4}\) = _____ \(\frac{□}{□}\)
Answer:
7 \(\frac{1}{2}\)
Explanation:
1 \(\frac{2}{4}\) = 6/4
5 x 6/4 = 30/4 = 15/2. 15/2 = 7 and remainder 1. So, 15/2 = 7 1/2
Question 10.
4 × 2 \(\frac{2}{5}\) = _____ \(\frac{□}{□}\)
Answer:
9\(\frac{3}{5}\)
Explanation:
2 \(\frac{2}{5}\) = 12/5
4 x 12/5 = 48/5. 48/5 = 9 and remainder 3. So, 48/5 = 9 3/5
Look for a Pattern Algebra Write the unknown number.


Question 13.
3 × □ \(\frac{3}{8}\) = 4 \(\frac{1}{8}\)
□ = ______
Answer:
1
Explanation:
4 \(\frac{1}{8}\) = 33/8
Let the unknown number is s. If s is 1, 3 × 1 \(\frac{3}{8}\) = 3 x 11/8 = 33/8.
Question 14.
Describe two different ways to write \(\frac{7}{3}\) as a mixed number.
Type below:
_________
Answer:
One is 2\(\frac{1}{3}\)
Another one is 2 + 1/3
Explanation:
7/3 = 2 and the remainder is 1. So, 2 1/3 is one mixed fraction.
Seond method is 3/3 + 3/3 + 1/3 = 2 + 1/3.
Page No. 478
Use the recipe for 15–18.

Question 15.
Otis plans to make 3 batches of sidewalk chalk. How much plaster of Paris does he need?
______ \(\frac{□}{□}\) cups plaster of Paris
Answer:
4\(\frac{1}{2}\) cups plaster of Paris
Explanation:
1\(\frac{1}{2}\) = 3/2 + 3/2 + 3/2 = 9/2
9/2 = 4, the remainder is 1. So, 4 1/2 cups plaster of Paris need for 3 batches of sidewalk chalk.
Question 16.
What’s the Question? The answer is \(\frac{32}{3}\).
Type below:
_________
Answer:
How many tablespoons of powdered paint are needed for 4 batches of chalk?
Question 17.
Patty has 2 cups of warm water. Is that enough water to make 4 batches of sidewalk chalk? Explain how you know without finding the exact product.
______
Answer:
No. 4 x 1/2 = 2 and also 3/4 is greater than 1/2. So, 4 x 3/4 is greater than 2.
Question 18.
Rita makes sidewalk chalk 2 days a week. Each of those days, she spends 1 \(\frac{1}{4}\) hours making the chalk. How much time does Rita spend making sidewalk chalk in 3 weeks?
______ \(\frac{□}{□}\) hours
Answer:
7\(\frac{1}{2}\) hours
Explanation:
Rita makes sidewalk chalk 2 days a week. Each of those days, she spends 1 1/4 hours making the chalk.
1 week = 2 x 5/4 = 10/4 = 5/2.
3 weeks = 3 x 5/2 = 15/2 = 7 1/2.

Common Core – New – Page No. 479
Multiply a Fraction or Mixed Number by a Whole Number.
Multiply. Write the product as a mixed number.
Question 1.
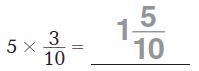
Answer:
1\(\frac{5}{10}\)
Explanation:
5 x 3/10 = 15/10 = 1 and remainder is 5. So, the mixed fraction is 1 5/10
Question 2.
3 × \(\frac{3}{5}\) =
______ \(\frac{□}{□}\)
Answer:
1\(\frac{4}{5}\)
Explanation:
3 x 3/5 = 9/5 = 1 and remainder is 4. So, the mixed fraction is 1 4/5
Question 3.
5 × \(\frac{3}{4}\) =
______ \(\frac{□}{□}\)
Answer:
3\(\frac{3}{4}\)
Explanation:
15/4 = 3 and remainder is 3. So, the mixed fraction is 3 3/4
Question 4.
4 × 1 \(\frac{1}{5}\) =
______ \(\frac{□}{□}\)
Answer:
4\(\frac{4}{5}\)
Explanation:
1 \(\frac{1}{5}\) = 6/5.
4 x 6/5 = 24/5 = 4 and the remainder is 4. So, the mixed fraction is 4 4/5


Question 7.
2 × 2 \(\frac{7}{8}\) =
______ \(\frac{□}{□}\)
Answer:
6\(\frac{1}{1}\)
Explanation:
2 \(\frac{7}{8}\) = 23/8
2 x 23/8 = 46/8 = 6 1/1
Question 8.
7 × 1 \(\frac{3}{4}\) =
______ \(\frac{□}{□}\)
Answer:
9\(\frac{3}{4}\)
Explanation:
1 \(\frac{3}{4}\) = 7/4
7 x 7/4 = 39/4
39/4 = 9 and the remainder is 3. So, the mixed fraction is 9 3/4
Question 9.
8 × 1 \(\frac{3}{5}\) =
______ \(\frac{□}{□}\)
Answer:
12\(\frac{4}{5}\)
Explanation:
1 \(\frac{3}{5}\) = 8/5
8 x 8/5 = 64/5
64/5 = 12 and the remainder is 4. So, the mixed fraction is 12 4/5
Problem Solving


Common Core – New – Page No. 480
Lesson Check
Question 1.
A mother is 1 \(\frac{3}{4}\) times as tall as her son. Her son is 3 feet tall. How tall is the mother?
Options:
a. 4 \(\frac{3}{4}\) feet
b. 5 \(\frac{1}{4}\) feet
c. 5 \(\frac{1}{2}\) feet
d. 5 \(\frac{3}{4}\) feet
Answer:
b. 5 \(\frac{1}{4}\) feet
Explanation:
A mother is 1 3/4 times as tall as her son. Her son is 3 feet tall.
So, 3 x 7/4 = 21/4 = 5 and the remainder is 1. The mixed fraction is 5 1/4 feet.
Question 2.
The cheerleaders are making a banner that is 8 feet wide. The length of the banner is 1 \(\frac{1}{3}\) times the width of the banner. How long is the banner?
Options:
a. 8 \(\frac{1}{3}\) feet
b. 8 \(\frac{3}{8}\) feet
c. 10 \(\frac{1}{3}\) feet
d. 10 \(\frac{2}{3}\) feet
Answer:
d. 10 \(\frac{2}{3}\) feet
Explanation:
The cheerleaders are making a banner that is 8 feet wide. he length of the banner is 1 1/3 times the width of the banner.
So, 8 x 4/3 = 32/3 =10 and the remainder is 2. The mixed fraction is 10 2/3 feet.
Spiral Review
Question 3.
Karleigh walks \(\frac{5}{8}\) mile to school every day. How far does she walk to school in 5 days?
Options:
a. \(\frac{5}{40}\) mile
b. \(\frac{25}{40}\) mile
c. \(\frac{10}{8}\) miles
d. \(\frac{25}{8}\) miles
Answer:
d. \(\frac{25}{8}\) miles
Explanation:
5 x 5/8 = 25/8.
Question 4.
Which number is a multiple of \(\frac{4}{5}\)?
Options:
a. \(\frac{8}{10}\)
b. \(\frac{12}{15}\)
c. \(\frac{16}{20}\)
d. \(\frac{12}{5}\)
Answer:
d. \(\frac{12}{5}\)
Explanation:
The multiple of \(\frac{4}{5}\) has the denominator 5. So, \(\frac{12}{5}\) is the correct answer.
Question 5.
Jo cut a key lime pie into 8 equal-size slices. The next day, \(\frac{7}{8}\) of the pie is left. Jo puts each slice on its own plate. How many plates does she need?
Options:
a. 5
b. 6
c. 7
d. 8
Answer:
c. 7
Explanation:
Jo cut a key lime pie into 8 equal-size slices. The next day, \(\frac{7}{8}\) of the pie is left. Jo puts each slice on its own plate. She needs 7 plates.
Question 6.
Over the weekend, Ed spent 1 \(\frac{1}{4}\) hours doing his math homework and 1 \(\frac{3}{4}\) hours doing his science project. Altogether, how much time did Ed spend doing homework over the weekend?
Options:
a. 3 hours
b. 2 \(\frac{3}{4}\) hours
c. 2 \(\frac{1}{2}\) hours
d. 2 hours
Answer:
a. 3 hours
Explanation:
5/4 + 7/4 = 12/4 = 3 hours
Page No. 483
Question 1.
Komodo dragons are the heaviest lizards on Earth. A baby Komodo dragon is 1 \(\frac{1}{4}\) feet long when it hatches. Its mother is 6 times as long. How long is the mother?
First, draw a bar model to show the problem.
Type below:
_________
Answer:
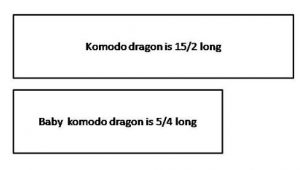
Question 1.
Then, write the equation you need to solve.
Type below:
_________
Answer:
A baby Komodo dragon is 5/4 feet.
Her mother is 6 x 5/4 = 30/4 feet long.
Question 1.
Finally, find the length of the mother Komodo dragon.
The mother Komodo dragon is _____ feet long.
______ \(\frac{□}{□}\)
Answer:
7\(\frac{2}{4}\)
Explanation:
30/4 = 7 and the remainder is 2. The mixed fraction is 7 2/4 feet.
Question 2.
What if a male Komodo dragon is 7 times as long as the baby Komodo dragon? How long is the male? How much longer is the male than the mother?
______ \(\frac{□}{□}\) feet long
______ \(\frac{□}{□}\) feet longer
Answer:
35/4 feet long
5/4 feet longer
Explanation:
If a male Komodo dragon is 7 times as long as the baby Komodo dragon, then 7 x 5/4 = 35/4.
35/4 – 30/4 = 5/4 feet male Komodo dragon is grater than female Komodo dragon.

Page No. 484
Use the table for 5 and 6.
Payton has a variety of flowers in her garden. The table shows the average heights of the flowers.
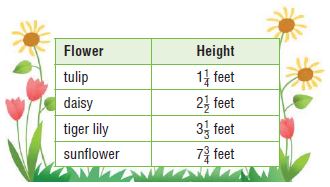
tulip = 5/4 = 1.25
daisy = 5/2 = 2.5
tiger lily = 10/3 = 3.33
sunflower = 31/4 = 7.75
Question 5.
Make Sense of Problems What is the difference between the height of the tallest flower and the height of the shortest flower in Payton’s garden?
______ \(\frac{□}{□}\) feet
Answer:
6\(\frac{2}{4}\) feet
Explanation:
tallest flower = sunflower
shortest flower = tulip
Difference between the tallest flower and shortest flower = 31/4 – 5/4 = 26/4 =6 and the remainder is 2. So, the mixed fraction is 6 2/4 feet.
Question 6.
Payton says her average sunflower is 7 times the height of her average tulip. Do you agree or disagree with her statement? Explain your reasoning.
Type below:
_________
Answer:
I will disagree with her statement. Tulip = 5/4. 7 x 5/4 = 35/4. 31/4 is smaller than 35/4. So, the statement is not correct.

Question 8.
The table shows the lengths of different types of turtles at a zoo.
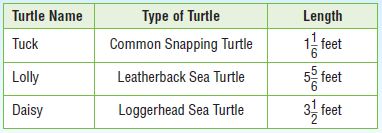
For numbers 8a–8d, select True or False for each statement.
a. Daisy is 4 times as long as Tuck.
i. True
ii. False
Answer:
ii. False
Explanation:
Tuck = 7/6
Lolly = 35/6
Daisy = 7/2
7/6 x 4 = 28/6.
So, the statement is false.
Question 8.
b. Lolly is 5 times as long as Tuck.
i. True
ii. False
Answer:
i. True
Explanation:
5 x 7/6 = 35/6.
So, the statement is true.
Question 8.
c. Daisy is 3 times as long as Tuck.
i. True
ii. False
Answer:
i. True
Explanation:
3 x 7/6 = 21/6 = 7/2
So, the statement is true.
Question 8.
d. Lolly is 2 times as long as Daisy.
i. True
ii. False
Answer:
ii. False
Explanation:
2 x 7/2 = 7.
So, the statement is false.
Common Core – New – Page No. 485
Problem Solving Comparison
Problems with Fractions
Read each problem and solve.
Question 1.
A shrub is 1 \(\frac{2}{3}\) feet tall. A small tree is 3 times as tall as the shrub. How tall is the tree?

Answer:
5 feet
Explanation:

Question 2.
You run 1 \(\frac{3}{4}\) miles each day. Your friend runs 4 times as far as you do. How far does your friend run each day?
__________ miles
Answer:
7 miles
Explanation:
4 x 7/4 = 7 miles each day
Question 3.
At the grocery store, Ayla buys 1 \(\frac{1}{3}\) pounds of ground turkey. Tasha buys 2 times as much ground turkey as Ayla. How much ground turkey does Tasha buy?
______ \(\frac{□}{□}\) pounds
Answer:
2\(\frac{2}{3}\) pounds
Explanation:
2 x 4/3 = 8/3 = 2 and the remainder is 2. The mixed fraction is 2 2/3 pounds
Question 4.
When Nathan’s mother drives him to school, it takes \(\frac{1}{5}\) hour. When Nathan walks to school, it takes him 4 times as long to get to school. How long does it take Nathan to walk to school?
\(\frac{□}{□}\) hours
Answer:
\(\frac{4}{5}\) hours
Explanation:
4 x 1/5 = 4/5 hour
Common Core – New – Page No. 486
Lesson Check
Question 1.
A Wilson’s Storm Petrel is a small bird with a wingspan of 1 \(\frac{1}{3}\) feet. A California Condor is a larger bird with a wingspan almost 7 times as wide as the wingspan of the petrel. About how wide is the wingspan of the California Condor?
Options:
a. \(\frac{4}{21}\) foot
b. 2 \(\frac{1}{3}\) feet
c. 7 \(\frac{1}{3}\) feet
d. 9 \(\frac{1}{3}\) feet
Answer:
d. 9 \(\frac{1}{3}\) feet
Explanation:
1 1/3 = 4/3.
7 x 4/3 = 28/3 feet = 9 and the remainder is 1. The mixed fraction is 9 1/3
Question 2.
The walking distance from the Empire State Building in New York City to Times Square is about \(\frac{9}{10}\) mile. The walking distance from the Empire State Building to Sue’s hotel is about 8 times as far. About how far is Sue’s hotel from the Empire State Building?
Options:
a. \(\frac{9}{80}\) mile
b. \(\frac{72}{80}\) mile
c. 1 \(\frac{7}{10}\) miles
d. 7 \(\frac{2}{10}\) miles
Answer:
d. 7 \(\frac{2}{10}\) miles
Explanation:
8 x 9/10 mile = 72/10 mile = 7 and the remainder is 2. The mixed fraction is 7 2/10 miles.
Spiral Review
Question 3.
Which of the following expressions is NOT equal to 3 × 2 \(\frac{1}{4}\)?
Options:
a. 3 × \(\frac{9}{4}\)
b. (3 × 2) + (3 × \(\frac{1}{4}\))
c. 6 \(\frac{3}{4}\)
d. 3 × 2 + \(\frac{1}{4}\)
Answer:
d. 3 × 2 + \(\frac{1}{4}\)
Explanation:
3 × 2 \(\frac{1}{4}\) = 3 x 9/4 = 27/4
a. 3 × \(\frac{9}{4}\) = 27/4
b. (3 × 2) + (3 × \(\frac{1}{4}\)) = 6 + 3/4 = 27/4
c. 6 \(\frac{3}{4}\) = 27/4
d. 3 × 2 + \(\frac{1}{4}\) = 6 + 1/4 = 25/4
Question 4.
At a bake sale, Ron sells \(\frac{7}{8}\) of an apple pie and \(\frac{5}{8}\) of a cherry pie. Altogether, how much pie does he sell at the bake sale?
Options:
a. \(\frac{2}{8}\)
b. \(\frac{12}{16}\)
c. \(\frac{12}{8}\)
d. \(\frac{35}{8}\)
Answer:
c. \(\frac{12}{8}\)
Explanation:
7/8 + 5/8 = 12/8
The bake sale 12/8 pie.
Question 5.
On a ruler, which measurement is between \(\frac{3}{16}\) inch and \(\frac{7}{8}\) inch?
Options:
a. \(\frac{1}{16}\) inch
b. \(\frac{1}{8}\) inch
c. \(\frac{11}{16}\) inch
d. \(\frac{15}{16}\) inch
Answer:
c. \(\frac{11}{16}\) inch
Question 6.
Which of the following numbers is composite?
Options:
a. 4
b. 3
c. 2
d. 1
Answer:
a. 4
Explanation:
4 has more than 2 factors.
Page No. 487

Question 2.
Marta is making 3 servings of fruit salad. She adds \(\frac{3}{8}\) cup blueberries for each serving. Her measuring cup holds \(\frac{1}{8}\) cup. How many times must Marta measure \(\frac{1}{8}\) cup of blueberries to have enough for the fruit salad? Shade the models to show your answer.
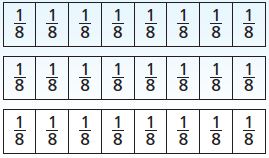
Marta must measure \(\frac{1}{8}\) _________ cup times.
_________
Answer:
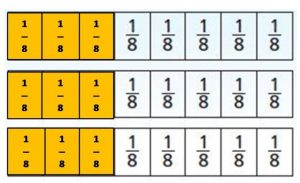
Marta must measure \(\frac{1}{8}\) 9 cup times.
Page No. 488
Question 4.
Molly is baking for the Moms and Muffins event at her school. She will bake 4 batches of banana muffins. She needs 1 \(\frac{3}{4}\) cups of bananas for each batch of muffins.
Part A
Molly completed the multiplication below and said she needed 8 cups of bananas for 4 batches of muffins. What is Molly’s error?
\(4 \times 1 \frac{3}{4}=4 \times \frac{8}{4}=\times \frac{32}{4}=8\)
Type below:
_________
Answer:
4 x 1 3/4 = 4 x 8/4 = 8
Molly did not write the mixed number, 1 3/4 as a fraction correctly. 1 3/4 is not equal to 8/4.
Question 4.
Part B
What is Molly’s correct number of cups for 4 batches of muffins? Explain how you found your answer.
_____ cups
Answer:
7 cups
Explanation:
She will bake 4 batches of banana muffins. She needs 7/4 cups of bananas for each batch of muffins.
So, if she prepares 4 batches of muffins = 4 x 7/4 = 7 cups of banana.
Question 5.
Which fraction is a multiple of \(\frac{1}{9}\)? Mark all that apply.
Options:
a. \(\frac{3}{9}\)
b. \(\frac{9}{12}\)
c. \(\frac{2}{9}\)
d. \(\frac{4}{9}\)
e. \(\frac{9}{10}\)
f. \(\frac{9}{9}\)
Answer:
a. \(\frac{3}{9}\)
c. \(\frac{2}{9}\)
d. \(\frac{4}{9}\)
f. \(\frac{9}{9}\)
Explanation:
The multiples of \(\frac{1}{9}\) have the denominator of 9.
Question 7.
Theo is comparing shark lengths. He learned that a horn shark is 2 \(\frac{3}{4}\) feet long. A blue shark is 4 times as long. Complete the model. Then find the length of a blue shark.
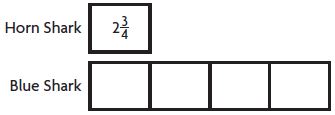
A blue shark is ____ feet long.
_____
Answer:
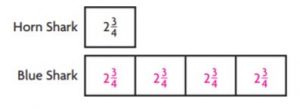
4 x 11/4 = 11.
A blue shark is 11 feet long.
Page No. 489
Question 8.
Joel made a number line showing the multiples of \(\frac{3}{5}\).
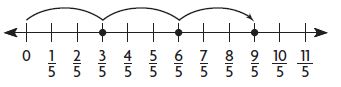
The product 2 × \(\frac{3}{5}\) is shown by the fraction _________ on the number line.
\(\frac{□}{□}\)
Answer:
The product 2 × \(\frac{3}{5}\) is shown by the fraction \(\frac{6}{5}\) on the number line.
Question 9.
Bobby has baseball practice Monday, Wednesday, and Friday. Each practice is 2 \(\frac{1}{2}\) hours. Bobby says he will have practice for 4 hours this week.
Part A
Without multiplying, explain how you know Bobby is incorrect.
Type below:
_________
Answer:
Bobby needs to find 3 × 2 1/2. If he estimates 3 × 2 hours, then he finds the practice is at least 6 hours. 6 is greater than 4, so Bobby’s answer is incorrect.
Question 9.
Part B
How long will Bobby have baseball practice this week? Write your answer as a mixed number. Show your work.
______ \(\frac{□}{□}\) hours
Answer:
7\(\frac{1}{2}\) hours
Explanation:
3 x 2 1/2 = 3 x 5/2 = 15/2 = 7 1/2
Question 10.
Look at the number line. Write the missing fractions.
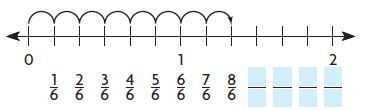
Type below:
_________
Answer:
9/6, 10/6, 11/6, 12/6
Question 11.
Ana’s dachshund weighed 5 \(\frac{5}{8}\) pounds when it was born. By age 4, the dog weighed 6 times as much. Fill each box with a number or symbol from the list to show how to find the weight of Ana’s dog at age 4. Not all numbers and symbols may be used.


Type below:
_________
Answer:

Page No. 490
Question 12.
Asta made a fraction number line to help her find 3 × \(\frac{4}{5}\).
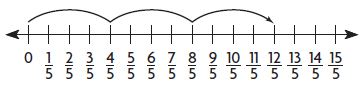
Select a way to write 3 × \(\frac{4}{5}\) as the product of a whole number and a unit fraction.

Type below:
_________
Answer:

12 × \(\frac{1}{5}\)
Explanation:
3 x 4/5 = 12/5 = 12 x 1/5.
Question 13.
Yusif wanted to give \(\frac{1}{3}\) of his total toy car collection to 2 of his friends. How many of his toy cars will he give away?
\(\frac{□}{□}\)
Answer:
\(\frac{2}{3}\)
Explanation:
Yusif wanted to give \(\frac{1}{3}\) of his total toy car collection to 2 of his friends. He has three toy cars in total. He has given 2 cars out of 3 cars. So, the answer is \(\frac{2}{3}\).
Question 14.
Select the correct product for the equation.

4 × \(\frac{5}{8}\) = □ 4 × \(\frac{4}{8}\) = □
Type below:
_________
Answer:
4 × \(\frac{5}{8}\) = \(\frac{20}{8}\)
4 × \(\frac{4}{8}\) = \(\frac{16}{8}\)
Page No. 491
Question 15.
The lengths of different types of snakes at a zoo are shown in the table.
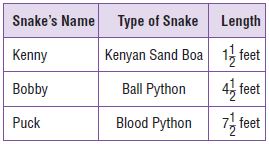
For numbers 15a–15d, select True or False for the statement.
a. Bobby is 4 times as long as Kenny.
i. True
ii. False
Answer:
ii. False
Explanation:
Kenny = 3/2
Bobby = 9/2
Puck = 15/2
4 x 3/2 =6
So, the statement is false.
Question 15.
b. Bobby is 3 times as long as Kenny.
i. True
ii. False
Answer:
i. True
Explanation:
3 x 3/2 = 9/2
So, the statement is true.
Question 15.
c. Puck is 5 times as long as Kenny.
i. True
ii. False
Answer:
i. True
Explanation:
5 x 3/2 = 15/2
So, the statement is true.
Question 15.
d. Puck is 2 times as long as Bobby.
i. True
ii. False
Answer:
ii. False
Explanation:
2 x 9/2 = 9
So, the statement is false.

Question 17.
Jess made a big kettle of rice and beans. He used 1 \(\frac{1}{2}\) cups of beans. He used 4 times as much rice.
Part A
Draw a model to show the problem.
Type below:
_________
Answer:
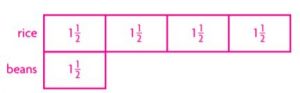
Question 17.
Part B
Use your model to write an equation. Then solve the equation to find the amount of rice Jess needs.
Type below:
_________
Answer:
6 cups
Explanation:
Rice = 4 x 3/2 = 12/2 = 6.
Jess needs 6 cups of rice.
Page No. 492
Question 18.
Mrs. Burnham is making modeling clay for her class. She needs \(\frac{2}{3}\) cup of warm water for each batch.
Part A
Mrs. Burnham has a 1-cup measure that has no other markings. Can she make 6 batches of modeling clay using only the 1-cup measure? Describe two ways you can find the answer.
Type below:
_________
Answer:
Yes. She needs 6 x 2/3 cups of water. 6 x 2/3 = 12/3 = 4 cups.
So, she can use the 1-cup measure 4 times to make 6 batches.
Question 18.
Part B
The modeling clay recipe also calls for \(\frac{1}{2}\) cup of cornstarch. Nikki says Mrs. Burnham will also need 4 cups of cornstarch. Do you agree or disagree? Explain.
Type below:
_________
Answer:
Disagree; 6 x 1/2 = 3 cups of cornstrach.
She doesn’t need 4 cups of cornstarch.
Question 19.
Donna buys some fabric to make place mats. She needs \(\frac{1}{5}\) yard of each type of fabric. She has 9 different types of fabrics to make her design. Use the following equation. Write the number in the box to make the statement true.
\(\frac{9}{5}\) = ______ × \(\frac{1}{5}\)
Answer:
9


Page No. 497
Question 1.
Write five-tenths as a fraction and as a decimal.
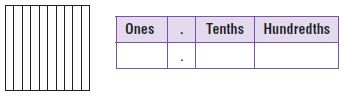
Fraction: __________ Decimal: __________
Type below:
_________
Answer:
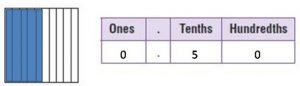
5/10 = 0.5
Write the fraction or mixed number and the decimal shown by the model.
Question 2.

Type below:
_________
Answer:
3\(\frac{2}{10}\)
three and two-tenths
Question 3.
Type below:
_________
Answer:
\(\frac{8}{10}\)
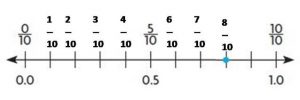
Write the fraction or mixed number and the decimal shown by the model.
Question 4.

Type below:
_________
Answer:
4/10 = 0.4
Explanation:
4 boxes are shaded out of 10 boxes. So, the fraction is 4/10.
Question 5.
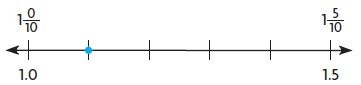
Type below:
_________
Answer:
1\(\frac{2}{10}\)
Question 6.
Type below:
_________
Answer:
2\(\frac{9}{10}\)
Question 7.
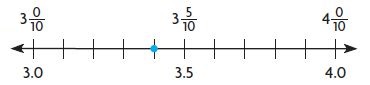
Type below:
_________
Answer:
3\(\frac{4}{10}\)
Practice: Copy and Solve Write the fraction or mixed number as a decimal.
Question 8.
5 \(\frac{9}{10}\) = _____
Answer:
\(\frac{59}{10}\)
Explanation:
Multiply 10 x 5 = 50.
Add 50 + 9 = 59.
The fraction is 59/10
Question 9.
\(\frac{1}{10}\) = _____
Answer:
0.1
Question 10.
\(\frac{7}{10}\) = _____
Answer:
0.7
Question 11.
8 \(\frac{9}{10}\) = _____
Answer:
\(\frac{89}{10}\)
Explanation:
Multiply 10 x 8 = 80.
Add 80 + 9 = 89.
The fraction is 89/10
Question 12.
\(\frac{6}{10}\) = _____
Answer:
0.6
Question 13.
6 \(\frac{3}{10}\) = _____
Answer:
\(\frac{63}{10}\)
Explanation:
Multiply 10 x 6 = 60.
Add 60 + 3 = 63.
The fraction is 63/10
Question 14.
\(\frac{5}{10}\) = _____
Answer:
0.5
Question 15.
9 \(\frac{7}{10}\) = _____
Answer:
\(\frac{97}{10}\)
Explanation:
Multiply 10 x 9 = 90.
Add 90 +7 = 97.
The fraction is 97/10
Page No. 498
Use the table for 16−19.

Question 16.
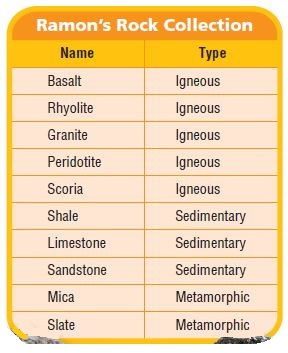
What part of the rocks listed in the table are igneous? Write your answer as a decimal.
_____
Answer:
0.5
Question 17.
Sedimentary rocks make up what part of Ramon’s collection? Write your answer as a fraction and in word form.
Type below:
_________
Answer:
3/10 and three-tenths
Question 18.
What part of the rocks listed in the table are metamorphic? Write your answer as a fraction and as a decimal.
Type below:
_________
Answer:
2/10 or 0.2
Question 19.
Communicate Niki wrote the following sentence in her report: “Metamorphic rocks make up 2.0 of Ramon’s rock collection.” Describe her error.
Type below:
_________
Answer:
Metamorphic rocks make up 2.0 of Ramon’s rock collection. But from the given table, it is clearly mentioned that the answer is 0.2. So, she made a mistake to make up Ramon’s rock collection.
Question 20.
Josh paid for three books with two $20 bills. He received $1 in change. Each book was the same price. How much did each book cost?
$ _____ each book
Answer:
$19/3 for each book.
Explanation:
Josh paid for three books with two $20 bills. He received $1 in change. So, he paid $19 for three books. As the each book has same price, the answer is $19/3 for each book.
Question 21.
Select a number shown by the model. Mark all that apply.
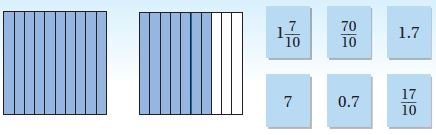
Type below:
_________
Answer:
1\(\frac{7}{10}\)
1.7
Conclusion:
We understand the knowledge shed regarding Go Math Grade 4 Answer Key Chapter 8 Multiply Fractions by Whole Numbers PDF has benefited you more. If you have any queries you can examine your knowledge using the Grade 4 Chapter 8 Answer Key Homework Practice FL. Visit our site to ask for details about the Go Math Solution Key of different grades.
