Are you searching for the Go Math Grade 6 Solution Key for Chapter 8 Solutions of Equations? If my guess is correct then you are on the right page. We provide the solutions to all the questions in pdf format. So, Download Go Math 6th Grade Answer Key Chapter 6 Chapter 8 Solutions of Equations pdf for free. Our Go Math Grade 6 Answer Key Chapter 8 Solutions of Equations is helpful for quick and easy learning.
Go Math Grade 6 Answer Key Chapter 8 Solutions of Equations
Enhance your performance in practice tests or assignments with the help of HMH Go Math 6th Grade Answer Key Chapter 8 Solutions of Equations. Get the solutions of Review Test and Mid Chapter Checkpoint in Go Math 6th Grade Chapter 8 Solutions of Equations. Scroll down this page to know the topics covered in this chapter. Make use of the links and Download Grade 6 Go Math Answer Key Chapter 8 Solutions of Equations.
Lesson 1: Solutions of Equations
- Share and Show – Page No. 423
- Problem Solving + Applications – Page No. 424
- Solutions of Equations – Page No. 425
- Lesson Check – Page No. 426
Lesson 2: Write Equations
- Share and Show – Page No. 429
- Problem Solving + Applications – Page No. 430
- Write Equations – Page No. 431
- Lesson Check – Page No. 432
Lesson 3: Investigate • Model and Solve Addition Equations
- Share and Show – Page No. 435
- Problem Solving + Applications – Page No. 436
- Model and Solve Addition Equations – Page No. 437
- Lesson Check – Page No. 438
Lesson 4: Solve Addition and Subtraction Equations
- Share and Show – Page No. 441
- Unlock the Problem – Page No. 442
- Solve Addition and Subtraction Equations – Page No. 443
- Lesson Check – Page No. 444
Lesson 5: Investigate • Model and Solve Multiplication Equations
- Share and Show – Page No. 447
- Page No. 448
- Model and Solve Multiplication Equations – Page No. 449
- Lesson Check – Page No. 450
Lesson 6: Solve Multiplication and Division Equations
- Share and Show – Page No. 453
- Problem Solving + Applications – Page No. 454
- Solve Multiplication and Division Equations – Page No. 455
- Lesson Check – Page No. 456
Lesson 7: Problem Solving • Equations with Fractions
- Share and Show – Page No. 459
- On Your Own – Page No. 460
- Problem Solving Equations with Fractions – Page No. 461
- Lesson Check – Page No. 462
Mid-Chapter Checkpoint
Lesson 8: Solutions of Inequalities
- Share and Show – Page No. 467
- Problem Solving + Applications – Page No. 468
- Solutions of Inequalities – Page No. 469
- Lesson Check – Page No. 470
Lesson 9: Write Inequalities
- Share and Show – Page No. 473
- Make Generalizations – Page No. 474
- Write Inequalities – Page No. 475
- Lesson Check – Page No. 476
Lesson 10: Graph Inequalities
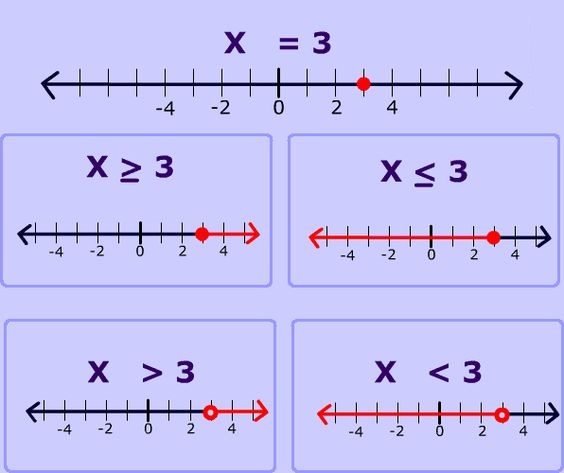
- Share and Show – Page No. 479
- Problem Solving + Applications – Page No. 480
- Graph Inequalities – Page No. 481
- Lesson Check – Page No. 482
Chapter 8 Review/Test
- Chapter 8 Review/Test – Page No. 483
- Chapter 8 Review/Test – Page No. 484
- Chapter 8 Review/Test Page No. 485
- Chapter 8 Review/Test – Page No. 486
- Chapter 8 Review/Test Page No. 487
- Chapter 8 Review/Test Page No. 488
Share and Show – Page No. 423
Determine whether the given value of the variable is a solution of the equation.
Question 1.
x + 12 = 29; x = 7
The variable is __________
Answer: not a solution
Explanation:
Substitute the value in the given equation
x + 12 = 29
If x = 7
7 + 12 = 29
19 ≠ 29
Thus the variable is not a solution.
Question 2.
n − 13 = 2; n = 15
The variable is __________
Answer: a solution
Explanation:
Substitute the value in the given equation
n = 15
n − 13 = 2
15 – 13 = 2
The variable is a solution.
Question 3.
\(\frac{1}{2}\)c = 14; c = 28
The variable is __________
Answer: a solution
Explanation:
Substitute the value in the given equation
c = 28
\(\frac{1}{2}\)c = 14
\(\frac{1}{2}\) × 28 = 14
14 = 14
Thus the variable is a solution.

Question 5.
d − 8.7 = 6; d = 14.7
The variable is __________
Answer: a solution
Explanation:
Substitute the value in the given equation
d = 14.7
d − 8.7 = 6
14.7 – 8.7 = 6
6 = 6
Thus the variable is a solution.

On Your Own
Determine whether the given value of the variable is a solution to the equation.
Question 7.
17.9 + v = 35.8; v = 17.9
The variable is __________
Answer: a solution
Explanation:
Substitute the value in the given equation
17.9 + v = 35.8
v = 17.9
17.9 + 17.9 = 35.8
35.8 = 35.8
Thus the variable is a solution.
Question 8.
c + 35 = 57; c = 32
The variable is __________
Answer: not a solution
Explanation:
Substitute the value in the given equation
c + 35 = 57
c = 32
32 + 35 = 57
67 ≠ 57
Thus the variable is not a solution.
Question 9.
18 = \(\frac{2}{3}\)h; h= 12
The variable is __________
Answer: not a solution
Explanation:
Substitute the value in the given equation
18 = \(\frac{2}{3}\)h
h = 12
\(\frac{2}{3}\) × 12 = 8
18 ≠ 8
Thus the variable is not a solution.


Question 11.
Antonio ran a total of 9 miles in two days. On the first day he ran 5 \(\frac{1}{4}\) miles. The equation 9 – d = 5 \(\frac{1}{4}\) can be used to find the distance d in miles Antonio ran the second day. Determine whether d = 4 \(\frac{3}{4}\), d = 4, or d = 3 \(\frac{3}{4}\) is a solution of the equation, and tell what the solution means.
The solution is ________ \(\frac{□}{□}\)
Answer: 3 \(\frac{3}{4}\)
Explanation:
9 – d = 5 \(\frac{1}{4}\)
Substitute d = 4 \(\frac{3}{4}\) in the above equation
9 – 4 \(\frac{3}{4}\) = 5 \(\frac{1}{4}\)
4 \(\frac{1}{4}\) ≠ 5 \(\frac{1}{4}\)
Not a solution
Substitute d = 4
9 – 4 = 5 \(\frac{1}{4}\)
5 ≠ 5 \(\frac{1}{4}\)
Not a solution
Substitute d = 3 \(\frac{3}{4}\)
9 – 3 \(\frac{3}{4}\) = 5 \(\frac{1}{4}\)
5 \(\frac{1}{4}\) = 5 \(\frac{1}{4}\)
9 – d = 5 \(\frac{1}{4}\); d = 3 \(\frac{3}{4}\) is a solution.
Problem Solving + Applications – Page No. 424
Use the table for 12–14.
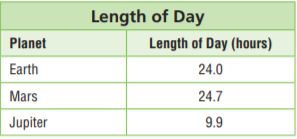
Question 12.
Connect Symbols and Words The length of a day on Saturn is 14 hours less than a day on Mars. The equation 24.7 − s = 14 can be used to find the length in hours s of a day on Saturn. Determine whether s = 9.3 or s = 10.7 is a solution of the equation, and tell what the solution means.
Type below:
_____________
Answer: s = 10.7
Explanation:
The length of a day on Saturn is 14 hours less than a day on Mars.
The equation 24.7 − s = 14 can be used to find the length in hours s of a day on Saturn.
24.7 − s = 14
Substitute s = 9.3 in the equation
24.7 – 9.3 = 14
15.4 ≠ 14
Not a solution
Substitute s = 10.7 in the equation
24.7 – 10.7 = 14
14 = 14
Therefore s = 10.7 is a solution to the equation.
Question 13.
A storm on one of the planets listed in the table lasted for 60 hours, or 2.5 of the planet’s days. The equation 2.5h = 60 can be used to find the length in hours h of a day on the planet. Is the planet Earth, Mars, or Jupiter? Explain.
Type below:
_____________
Answer: Earth
Explanation:
A storm on one of the planets listed in the table lasted for 60 hours, or 2.5 of the planet’s days.
2.5h = 60
h = 60/2.5
h = 24 hours
By seeing the above table we can say that Earth is the answer.
Question 14.
A day on Pluto is 143.4 hours longer than a day on one of the planets listed in the table. The equation 153.3 − p = 143.4 can be used to find the length in hours p of a day on the planet. What is the length of a storm that lasts \(\frac{1}{3}\) of a day on this planet?
________ hours
Answer: 3.3 hours
Explanation:
A day on Pluto is 143.4 hours longer than a day on one of the planets listed in the table.
153.3 − p = 143.4
153.3 – 143.4 = p
p = 153.3 – 143.4
p = 9.9
Now p with \(\frac{1}{3}\) to find the length of a storm that lasts a day on this planet
9.9 × \(\frac{1}{3}\) = 3.3 hours

Question 16.
The marking period is 45 school days long. Today is the twenty-first day of the marking period. The equation x + 21 = 45 can be used to find the number of days x left in the marking period. Using substitution, Rachel determines there are _____ days left in the marking period.
Rachel determines there are _____________ days left.
Answer: 24
Explanation:
The marking period is 45 school days long. Today is the twenty-first day of the marking period.
The equation x + 21 = 45
x = 45 – 21 = 24 days
Using substitution, Rachel determines there are 24 days left in the marking period.
Thus Rachel determines there are 24 days left.
Solutions of Equations – Page No. 425
Determine whether the given value of the variable is a solution of the equation.
Question 1.
x − 7 = 15; x = 8
The variable is __________
Answer: not a solution
Explanation:
Substitute the value in the given equation.
x = 8
8 – 7 = 15
1 ≠ 15
Therefore the variable is not a solution.

Question 3.
\(\frac{1}{3}\)h = 6; h = 2
The variable is __________
Answer: not a solution
Explanation:
Substitute the value in the given equation.
\(\frac{1}{3}\)h = 6
h = 2
\(\frac{1}{3}\) × 2 = 6
\(\frac{2}{3}\) ≠ 6
Therefore the variable is not a solution.
Question 4.
16.1 + d = 22; d = 6.1
The variable is __________
Answer: not a solution
Explanation:
Substitute the value in the given equation.
16.1 + d = 22
d = 6.1
16.1 + 6.1 = 22
22.2 ≠ 22
Therefore the variable is not a solution.
Question 5.
9 = \(\frac{3}{4}\)e; e = 12
The variable is __________
Answer: a solution
Explanation:
Substitute the value in the given equation.
9 = \(\frac{3}{4}\)e
e = 12
9 = \(\frac{3}{4}\)(12)
9 = 3 × 3
9 = 9
Therefore the variable is a solution.

Problem Solving
Question 7.
Terrance needs to score 25 points to win a game. He has already scored 18 points. The equation 18 + p = 25 can be used to find the number of points p that Terrance still needs to score. Determine whether p = 7 or p = 13 is a solution of the equation, and tell what the solution means.
Type below:
_____________
Answer: p = 7
Explanation:
Terrance needs to score 25 points to win a game. He has already scored 18 points.
The equation is 18 + p = 25
Substitute p = 7 in the above equation.
18 + 7 = 25
25 = 25
The variable is a solution.
Substitute p = 13
18 + p = 25
18 + 13 = 25
31 ≠ 25
The variable is not a solution.
Therefore p = 7 is a solution for the equation.
Question 8.
Madeline has used 50 sheets of a roll of paper towels, which is \(\frac{5}{8}\) of the entire roll. The equation \(\frac{5}{8}\)s = 50 can be used to find the number of sheets s in a full roll. Determine whether s = 32 or s = 80 is a solution of the equation, and tell what the solution means.
Type below:
_____________
Answer:
Madeline has used 50 sheets of a roll of paper towels, which is \(\frac{5}{8}\) of the entire roll.
\(\frac{5}{8}\)s = 50
s = 50 × \(\frac{8}{5}\)
s = 80 because 80 × 5 = 400
400 ÷ 8 = 50

Lesson Check – Page No. 426
Question 1.
Sheena received a gift card for $50. She has already used it to buy a lamp for $39.99. The equation 39.99 + x = 50 can be used to find the amount x that is left on the gift card. What is the solution to the equation?
_____
Answer: 10.01
Explanation:
Given:
Sheena received a gift card for $50. She has already used it to buy a lamp for $39.99.
The equation 39.99 + x = 50
39.99 + x = 50
x = 50 – 39.99
x = 50.00 – 39.99
x = 10.01
Thus $10.01 is left on the gift card.
Question 2.
When Pete had a fever, his temperature was 101.4°F. After taking some medicine, his temperature was 99.2°F. The equation 101.4 – d = 99.2 can be used to find the number of degrees d that Pete’s temperature decreased. What is the solution of the equation?
_____
Answer: 2.2
Explanation:
Given,
When Pete had a fever, his temperature was 101.4°F.
After taking some medicine, his temperature was 99.2°F.
The equation 101.4 – d = 99.2
104.4 – 99.2 = d
d = 104.4 – 99.2
d = 2.2
Spiral Review


Question 5.
Andrew made p picture frames. He sold 2 of them at a craft fair. Write an expression that could be used to find the number of picture frames Andrew has left.
Type below:
_____________
Answer: p – 2
Explanation:
Andrew made p picture frames. He sold 2 of them at a craft fair.
The expression is the difference of 9 and 2
The equation is p – 2
Question 6.
Write an expression that is equivalent to 4 + 3(5 + x).
Type below:
_____________
Answer: 4 + 15 + 3x
Explanation:
4 + 3(5 + x) = 4 + 15 + 3x
3x + 19
Thus the expression 4 + 3(5 + x) is equivalent to 4 + 15 + 3x or 3x + 19
Share and Show – Page No. 429
Question 1.
Write an equation for the word sentence “25 is 13 more than a number.”
Type below:
_____________
Answer:
Let n represent the unknown number. The phrase ‘more than’ indicates an addition operation.
Thus the equation is 25 = 13 + n.
Write an equation for the word sentence.
Question 2.
The difference of a number and 2 is 3 \(\frac{1}{3}\).
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase “difference” indicates the subtraction operation.
The equation is n – 2 = 3 \(\frac{1}{3}\)

Write a word sentence for the equation.
Question 4.
x − 0.3 = 1.7
Type below:
_____________
Answer: The difference of x and 0.3 is 1.7
Question 5.
25 = \(\frac{1}{4}\)n
Type below:
_____________
Answer: 25 is n times \(\frac{1}{4}\)
Write an equation for the word sentence.
Question 6.
The quotient of a number and 20.7 is 9.
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase “quotient” indicates the division operation.
Thus the equation is n ÷ 20.7 = 9.
Question 7.
24 less than the number of snakes is 35.
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase “less than” indicates subtraction operation.
Thus the equation is n – 24 = 35
Question 8.
75 is 18 \(\frac{1}{2}\) more than a number.
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase “more than” indicates addition operation.
75 = 18 \(\frac{1}{2}\) + n
Question 9.
d degrees warmer than 50 degrees is 78 degrees.
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase “warmer than” indicates addition operation.
The equation is d + 50 = 78 degrees
Write a word sentence for the equation.
Question 10.
15g = 135
Type below:
_____________
Answer: g times 15 is 135
Question 11.
w ÷ 3.3 = 0.6
Type below:
_____________
Answer: The quotient of w and 3.3 is 0.6
Problem Solving + Applications – Page No. 430
To find out how far a car can travel on a certain amount of gas, multiply the car’s fuel efficiency in miles per gallon by the gas used in gallons. Use this information and the table for 12–13.
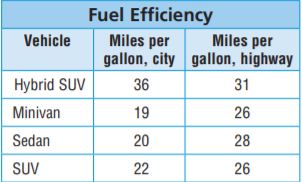
Question 12.
Write an equation that could be used to find how many miles a hybrid SUV can travel in the city on 20 gallons of gas.
Type below:
_____________
Answer:
From table 36 miles per gallon in the city.
A hybrid SUV uses 36 miles per gallon in the city.
So, no. of miles = y
x = no. of gallons
So, y = 36 × x
x = 20 gallons
Thus y = 36 × 20
Question 13.
A sedan traveled 504 miles on the highway on a full tank of gas. Write an equation that could be used to find the number of gallons the tank holds.
Type below:
_____________
Answer:
A sedan uses 28 miles per gallon on the highway.
The equation that could be used to find the number of gallons the tank holds is
504 = 28g
Question 14.
Connect Symbols to Words Sonya was born in 1998. Carmen was born 11 years after Sonya. If you wrote an equation to find the year in which Carmen was born, what operation would you use in your equation?
Type below:
_____________
Answer: In this equation, I would use addition or subtraction operation.
Question 15.
A magazine has 110 pages. There are 23 full-page ads and 14 half-page ads. The rest of the magazine consists of articles. Write an equation that can be used to find the number of pages of articles in the magazine.
Type below:
_____________
Answer:
The equation that can be used to find the number of pages of articles in the magazine is
23 + 14/2 + a = 110
where a represents the number of articles.
Question 16.
What’s the Error? Tony is traveling 560 miles to visit his cousins. He travels 313 miles the first day. He says that he can use the equation m − 313 = 560 to find the number of miles m he has left on his trip. Describe and correct Tony’s error.
Type below:
_____________
Answer:
Tony subtracted the number of miles traveled from the number of miles left.
Tony should have written m + 313 = 560
Question 17.
Jamie is making cookies for a bake sale. She triples the recipe in order to have enough cookies to sell. Jamie uses 12 cups of flour to make the triple batch. Write an equation that can be used to find out how much flour f is needed for one batch of cookies.
Type below:
_____________
Answer:
The equation that can be used to find out how much flour f is needed for one batch of cookies is 3f = 12
Write Equations – Page No. 431
Write an equation for the word sentence.
Question 1.
18 is 4.5 times a number.
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase “times” indicates the multiplication operation.
The equation is 18 = 4.5n

Question 3.
The difference of a number and \(\frac{2}{3}\) is \(\frac{3}{8}\).
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase “difference” indicates a subtraction operation.
The equation is n – \(\frac{2}{3}\) = \(\frac{3}{8}\)
Question 4.
A number divided by 0.5 is 29.
Type below:
_____________
Answer:
Let n represents the unknown number.
The phrase divided by indicates division operation.
The equation is n ÷ 0.5 = 29
Write a word sentence for the equation.
Question 5.
x − 14 = 52
Type below:
_____________
Answer:
14 less than x is 52
the difference of x and 14 is 52
14 fewer than a number is 52.
Question 6.
2.3m = 0.46
Type below:
_____________
Answer:
The product of 2.3 and m is 0.46
2.3 times m is .46
2.3 of m is 0.46
Question 7.
25 = k ÷ 5
Type below:
_____________
Answer: 25 is the quotient of k and 5.
Question 8.
\(4 \frac{1}{3}+q=5 \frac{1}{6}\)
Type below:
_____________
Answer:
The sum of \(4 \frac{1}{3}\) and q is [/latex]5 \frac{1}{6}[/latex]
q is more than \(4 \frac{1}{3}\) and [/latex]5 \frac{1}{6}[/latex]
\(4 \frac{1}{3}\) increased by a number is [/latex]5 \frac{1}{6}[/latex]
Question 9.
An ostrich egg weighs 2.9 pounds. The difference between the weight of this egg and the weight of an emu egg is 1.6 pounds. Write an equation that could be used to find the weight w, in pounds, of the emu egg.
Type below:
_____________
Answer: 2.9 – w = 1.6
Explanation:
An ostrich egg weighs 2.9 pounds.
The difference between the weight of this egg and the weight of an emu egg is 1.6 pounds.
The phrase “difference” indicates the subtraction operation.
The equation will be 2.9 – w = 1.6
Question 10.
In one week, the number of bowls a potter made was 6 times the number of plates. He made 90 bowls during the week. Write an equation that could be used to find the number of plates p that the potter made.
Type below:
_____________
Answer: 6p = 90
Explanation:
Given,
In one week, the number of bowls a potter made was 6 times the number of plates.
He made 90 bowls during the week.
The phrase “times” indicates the multiplication operation.
The equation to find the number of plates p that the potter made will be 6p = 90

Lesson Check – Page No. 432
Question 1.
Three friends are sharing the cost of a bucket of popcorn. The total cost of the popcorn is $5.70. Write an equation that could be used to find the amount ‘a’ in dollars that each friend should pay.
Type below:
_____________
Answer: 3a = 5.70
Explanation:
Three friends are sharing the cost of a bucket of popcorn.
The total cost of the popcorn is $5.70.
The expression will be “5.70 is the product of 3 and a.
The equation is 3a = 5.70
Question 2.
Salimah had 42 photos on her phone. After she deleted some of them, she had 23 photos left. What equation could be used to find the number of photos p that Salimah deleted?
Type below:
_____________
Answer: p + 23 = 42
Explanation:
Salimah had 42 photos on her phone. After she deleted some of them, she had 23 photos left.
The expression is the sum of p and 23 is 42.
Thus the equation is p + 23 = 42
Question 3.
A rope is 72 feet long. What is the length of the rope in yards?
______ yards
Answer: 24 yard
Explanation:
A rope is 72 feet long.
Convert from feet to yards.
1 yard = 3 feet
1 foot = 1/3 yards
72 feet = 72 × 1/3 = 24 yards
Thus the length of the rope is 24 yards.

Question 5.
The sides of a triangle have lengths s, s + 4, and 3s. Write an expression in the simplest form that represents the perimeter of the triangle.
Type below:
_____________
Answer: 5s + 4
Explanation:
The perimeter of the triangle is a + b + c
P = a + b + c
P = s + s + 4 + 3s
P = 5s + 4
Thus the perimeter of the triangle is 5s + 4
Question 6.
Gary knows that p = 2 \(\frac{1}{2}\) is a solution to one of the following equations. Which one has p = 2 \(\frac{1}{2}\) as its solution?
\(p+2 \frac{1}{2}=5\) \(p-2 \frac{1}{2}=5\)
\(2+p=2 \frac{1}{2}\) 4 – p = 2 \(\frac{1}{2}\)
Type below:
_____________
Answer: p + 2 \(\frac{1}{2}\) = 5
Explanation:
\(p+2 \frac{1}{2}=5\)
p + 2 \(\frac{1}{2}\) = 5
p = 5 – 2 \(\frac{1}{2}\)
p = 2 \(\frac{1}{2}\)
\(p-2 \frac{1}{2}=5\)
p – 2 \(\frac{1}{2}\) = 5
p = 5 + 2 \(\frac{1}{2}\)
p = 7 \(\frac{1}{2}\)
\(2+p=2 \frac{1}{2}\)
2 + p = 2 \(\frac{1}{2}\)
p = 2 \(\frac{1}{2}\) – 2
p = \(\frac{1}{2}\)
4 – p = 2 \(\frac{1}{2}\)
p = 4 – 2 \(\frac{1}{2}\)
p = 1 \(\frac{1}{2}\)
Share and Show – Page No. 435
Model and solve the equation by using algebra tiles or iTools.
Question 1.
x + 5 = 7
x = ______
Answer: 2
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 5 in the left rectangle, and model 7 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove five 1 tiles on the left side and five 1 tiles on the right side.
- The remaining titles will be two 1 tiles on the right sides.
Question 2.
8 = x + 1
x = ______
Answer: 7
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 1 in the left rectangle, and model 8 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove one 1 tiles on the left side and one 1 tiles on the right side.
- The remaining titles will be seven 1 tiles on the right sides.
Question 3.
x + 2 = 5
x = ______
Answer: 3
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 2 in the left rectangle, and model 5 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove two 1 tiles on the left side and five 1 tiles on the right side.
- The remaining titles will be three 1 tiles on the right sides.
Question 4.
x + 6 = 8
x = ______
Answer: 2
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 6 in the left rectangle, and model 8 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove six 1 tiles on the left side and six 1 tiles on the right side.
- The remaining titles will be two 1 tiles on the right sides.
Question 5.
5 + x = 9
x = ______
Answer: 4
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 5 in the left rectangle, and model 9 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove five 1 tiles on the left side and five 1 tiles on the right side.
- The remaining titles will be four 1 tiles on the right sides.
Question 6.
5 = 4 + x
x = ______
Answer: 1
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 4 in the left rectangle, and model 5 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove four 1 tiles on the left side and four 1 tiles on the right side.
- The remaining titles will be one 1 tiles on the right sides.
Solve the equation by drawing a model.
Question 7.
x + 1 = 5
x = ______
Answer: 4
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 1 in the left rectangle, and model 5 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove one 1 tiles on the left side and one 1 tiles on the right side.
- The remaining titles will be four 1 tiles on the right sides.
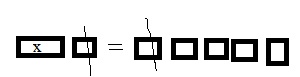
Question 8.
3 + x = 4
x = ______
Answer: 1
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 3 in the left rectangle, and model 4 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove three 1 tiles on the left side and three 1 tiles on the right side.
- The remaining titles will be one 1 tiles on the right sides.
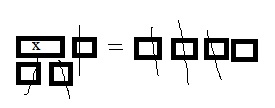
Question 9.
6 = x + 4
x = ______
Answer: 2
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 4 in the left rectangle, and model 6 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove four 1 tiles on the left side and four 1 tiles on the right side.
- The remaining titles will be two 1 tiles on the right sides.
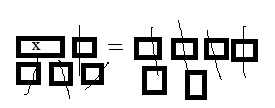
Question 10.
8 = 2 + x
x = ______
Answer: 6
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 2 in the left rectangle, and model 8 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove two 1 tiles on the left side and two 1 tiles on the right side.
- The remaining titles will be six 1 tiles on the right sides.
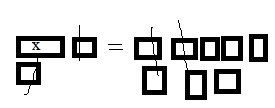
Question 11.
Describe a Method Describe how you would draw a model to solve the equation x + 5 = 10.
Type below:
_____________
Answer: x = 5
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 5 in the left rectangle, and model 10 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove five 1 tiles on the left side and five 1 tiles on the right side.
- The remaining titles will be five 1 tiles on the right sides.
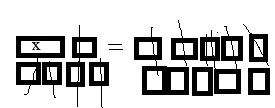
Problem Solving + Applications – Page No. 436
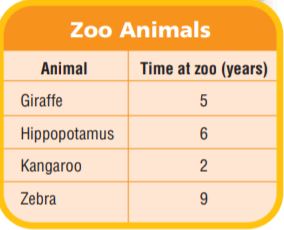
Question 12.
Interpret a Result The table shows how long several animals have lived at a zoo. The giraffe has lived at the zoo 4 years longer than the mountain lion. The equation 5 = 4 + y can be used to find the number of years y the mountain lion has lived at the zoo. Solve the equation. Then tell what the solution means.
Type below:
_____________
Answer:
The table shows how long several animals have lived in a zoo.
The giraffe has lived at the zoo 4 years longer than the mountain lion.
5 = 4 + y
y = 5 – 4
y = 1
The solution is y = 1
The solution means that the mountain lion has lived at the zoo for 1 year.
Question 13.
Carlos walked 2 miles on Monday and 5 miles on Saturday. The number of miles he walked on those two days is 3 miles more than the number of miles he walked on Friday. Write and solve an addition equation to find the number of miles Carlos walked on Friday
Type below:
_____________
Answer:
Given that,
Carlos walked 2 miles on Monday and 5 miles on Saturday.
The number of miles he walked on those two days is 3 miles more than the number of miles he walked on Friday.
The equation is f + 3 = 2 + 5
f + 3 = 7
f = 7 – 3
f = 4
The solution is f = 4
The solution means that Carlos walked 4 miles on Friday.
Question 14.
Sense or Nonsense? Gabriela is solving the equation x + 1 = 6. She says that the solution must be less than 6. Is Gabriela’s statement sense or nonsense? Explain.
Type below:
_____________
Answer: Gabriela’s statement makes sense.
x + 1 = 6
x = 6 – 1
x = 5
Thus the solution is less than 6.
Question 15.
The Hawks beat the Tigers by 5 points in a football game. The Hawks scored a total of 12 points.
Use numbers and words to explain how this model can be used to solve the equation x + 5 = 12.

Type below:
_____________
Answer:
Remove 5 squares from each side. The rectangle is by itself on the left and 7 squares are on the right side.
So, the solution is x = 7
Model and Solve Addition Equations – Page No. 437
Model and solve the equation by using algebra tiles.
Question 1.
x + 6 = 9
x = ________
Answer: 3
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 6 in the left rectangle, and model 9 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove six 1 tiles on the left side and six 1 tiles on the right side.
- The remaining titles will be three 1 tiles on the right sides.
Thus x = 3
Question 2.
8 + x = 10
x = ________
Answer: 2
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 8 in the left rectangle, and model 10 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove eight 1 tiles on the left side and eight 1 tiles on the right side.
- The remaining titles will be two 1 tiles on the right sides.
8 + x = 10
x = 10 – 8 = 2
x = 2
Question 3.
9 = x + 1
x = ________
Answer: 8
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 1 in the left rectangle, and model 9 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove 1 tile on the left side and 1 tile on the right side.
- The remaining titles will be eight 1 tiles on the right sides.
Thus x = 8
Solve the equation by drawing a model.
Question 4.
x + 4 = 7
x = ________
Answer: 3
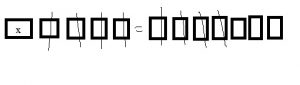
Question 5.
x + 6 = 10
x = ________
Answer: 4
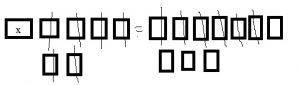
Problem Solving
Question 6.
The temperature at 10:00 was 10°F. This is 3°F warmer than the temperature at 8:00. Model and solve the equation x + 3 = 10 to find the temperature x in degrees Fahrenheit at 8:00.
Type below:
_____________
Answer: x = 7
Explanation:
The temperature at 10:00 was 10°F. This is 3°F warmer than the temperature at 8:00.
The equation is x + 3 = 10
x = 10 – 3 = 7
Question 7.
Jaspar has 7 more checkers left than Karen does. Jaspar has 9 checkers left. Write and solve an addition equation to find out how many checkers Karen has left.
Type below:
_____________
Answer: c = 2
Explanation:
Jaspar has 7 more checkers left than Karen does. Jaspar has 9 checkers left.
The expression is c + 7 = 9
The equation to find out how many checkers Karen has left is c + 7 = 9.
Question 8.
Explain how to use a drawing to solve an addition equation such as x + 8 = 40.
Type below:
_____________
Answer: 32
Explanation:
- Draw 2 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model x + 8 in the left rectangle, and model 40 in the right rectangle.
- To solve the equation, get the x tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove eight 1 tile on the left side and eight 1 tile on the right side.
- The remaining titles will be 32 1 tiles on the right side.
x + 8 = 40
x = 40 – 8
x = 32
Lesson Check – Page No. 438
Question 1.
What is the solution of the equation that is modeled by the algebra tiles?

x = ________
Answer: 1
The equation is x + 6 = 7
x = 7 – 6
x = 1

Spiral Review
Question 3.
A car’s gas tank has a capacity of 16 gallons. What is the capacity of the tank in pints?
________ pints
Answer: 128 pints
Explanation:
A car’s gas tank has a capacity of 16 gallons.
Convert from gallons to pints.
1 gallon = 8 pints
16 gallons = 16 × 8 = 128 pints
Thus the capacity of the tank is 128 pints.
Question 4.
Craig scored p points in a game. Marla scored twice as many points as Craig but 5 fewer than Nelson scored. How many points did Nelson score?
Type below:
_____________
Answer: 2p + 5
Explanation:
Craig scored p points in a game.
Marla scored twice as many points as Craig but 5 fewer than Nelson scored.
The equation will be 2p + 5.

Question 6.
The Empire State Building in New York City is 443.2 meters tall. This is 119.2 meters taller than the Eiffel Tower in Paris. Write an equation that can be used to find the height h in meters of the Eiffel Tower.
Type below:
_____________
Answer: 119.2 + h = 443.2
Explanation:
The Empire State Building in New York City is 443.2 meters tall.
This is 119.2 meters taller than the Eiffel Tower in Paris.
Here we have to use the addition operation.
The equation is 119.2 + h = 443.2
Share and Show – Page No. 441
Question 1.
Solve the equation n + 35 = 80.
n = ________
Answer: 45
Explanation:
The given equation is
n + 35 = 80
n = 80 – 35
n = 45
Solve the equation, and check the solution.
Question 2.
16 + x = 42
x = ________
Answer: 26
Explanation:
Given the equation 16 + x = 42
x + 16 = 42
x = 42 – 16
x = 26

Question 4.
m + \(\frac{3}{10}=\frac{7}{10}\)
m = \(\frac{□}{□}\)
Answer: \(\frac{4}{10}\)
Explanation:
The given equation is
m + \(\frac{3}{10}=\frac{7}{10}\)
m = \(\frac{7}{10}\) – \(\frac{3}{10}\)
The denominators are common so subtract the numerators
m = \(\frac{4}{10}\)
Question 5.
z – \(\frac{1}{3}=1 \frac{2}{3}\)
z = ________
Answer: 2
Explanation:
The given equation is
z – \(\frac{1}{3}=1 \frac{2}{3}\)
z = \(\frac{1}{3}\) + 1 \(\frac{2}{3}\)
z = 1 + \(\frac{1}{3}\) + \(\frac{2}{3}\)
z = 1 + \(\frac{3}{3}\)
z = 1 + 1 = 2
Thus the value of z is 2.
Question 6.
12 = x − 24
x = ________
Answer: 36
Explanation:
The given equation is
12 = x − 24
x – 24 = 12
x = 12 + 24
x = 36
Thus the value of x is 36.
Question 7.
25.3 = w − 14.9
w = ________
Answer: 40.2
Explanation:
The given equation is
25.3 = w − 14.9
w – 14.9 = 25.3
w = 25.3 + 14.9
w = 40.2
The value of w is 40.2
On Your Own
Practice: Copy and Solve Solve the equation, and check the solution.
Question 8.
y − \(\frac{3}{4}=\frac{1}{2}\)
y = _______ \(\frac{□}{□}\)
Answer: 1 \(\frac{1}{4}\)
Explanation:
The given equation is
y − \(\frac{3}{4}=\frac{1}{2}\)
y = \(\frac{1}{2}\) + \(\frac{3}{4}\)
y = 1 \(\frac{1}{4}\)
Therefore the value of y is 1 \(\frac{1}{4}\).
Question 9.
75 = n + 12
n = ________
Answer: 63
Explanation:
The given equation is
75 = n + 12
n + 12 = 75
n = 75 – 12
n = 63
The value of n is 63.
Question 10.
m + 16.8 = 40
m = ________
Answer: 23.2
Explanation:
The given equation is
m + 16.8 = 40
m = 40 – 16.8
m = 23.2
The value of m is 23.2
Question 11.
w − 36 = 56
w = ________
Answer: 92
Explanation:
The given equation is
w − 36 = 56
w = 56 + 36
w = 92
The value of w is 92.
Question 12.
8 \(\frac{2}{5}\) = d + 2\(\frac{2}{5}\)
d = ________
Answer: 6
Explanation:
The given equation is
8 \(\frac{2}{5}\) = d + 2\(\frac{2}{5}\)
d + 2\(\frac{2}{5}\) = 8 \(\frac{2}{5}\)
d = 8 \(\frac{2}{5}\) – 2\(\frac{2}{5}\)
d = 8 + \(\frac{2}{5}\) – 2 – \(\frac{2}{5}\)
d = 8 – 2 = 6
Thus the value of d is 6.
Question 13.
8.7 = r − 1.4
r = ________
Answer: 10.1
Explanation:
The given equation is
8.7 = r − 1.4
r − 1.4 = 8.7
r = 8.7 + 1.4
r = 10.1
The value of r is 10.1
Question 14.
The temperature dropped 8 degrees between 6:00 p.m. and midnight. The temperature at midnight was 26ºF. Write and solve an equation to find the temperature at 6:00 p.m.
________ ºF
Answer: 34ºF
Explanation:
The temperature dropped 8 degrees between 6:00 p.m. and midnight.
The temperature at midnight was 26ºF.
26ºF + 8ºF = 34ºF
The equation to find the temperature at 6:00 p.m is 34ºF
Question 15.
Reason Abstractly Write an addition equation that has the solution x = 9.
Type below:
_____________
Answer: x + 4 = 13
Explanation:
Let the equation be x + 4 = 13
x = 13 – 4
x = 9
Unlock the Problem – Page No. 442
Question 16.
In July, Kimberly made two deposits into her bank account. She made no withdrawals. At the end of July, her account balance was $120.62. Write and solve an equation to find Kimberly’s balance at the beginning of July.

a. What do you need to find?
Type below:
_____________
Answer: We need to find Kimberly’s balance at the beginning of July.
Question 16.
b. What information do you need from the bank statement?
Type below:
_____________
Answer: We need the information about the deposit on July 12 and July 25 from the bank statement.
Question 16.
c. Write an equation you can use to solve the problem. Explain what the variable represents.
Type below:
_____________
Answer:
x = bank account balance
y = deposit 1
z = deposit 2
x = y + z
Question 16.
d. Solve the equation. Show your work and describe each step.
Type below:
_____________
Answer: 120.62 = y + z
Where y is the deposit 1 and z represents the deposit 2.
y = $45.50, z = $43.24
45.50 + 43.24 = 88.74
x + 88.74 = 120.62
Question 16.
e. Write Kimberly’s balance at the beginning of July.
$ _______
Answer: 31.88
Explanation:
x + 88.74 = 120.62
x = 120.62 – 88.74
x = $31.88
Kimberly’s balance at the beginning of July is $31.88
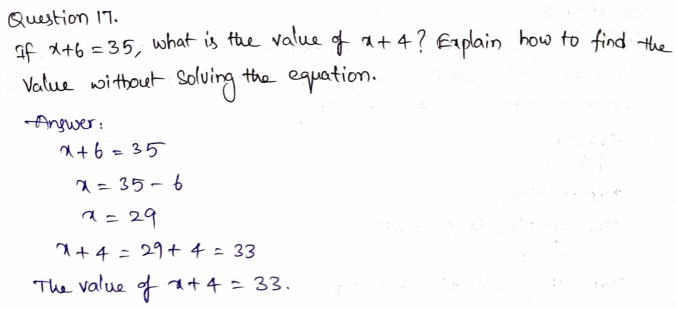
Question 18.
Select the equations that have the solution n = 23. Mark all that apply.
Options:
a. 16 + n = 39
b. n – 4 = 19
c. 25 = n – 2
d. 12 = n – 11
Answer: A, B, D
Explanation:
a. 16 + n = 39
n = 23
16 + 23 = 39
39 = 39
The variable is a solution.
b. n – 4 = 19
n = 23
23 – 4 = 19
19 = 19
The variable is a solution.
c. 25 = n – 2
25 = 23 – 2
25 ≠ 21
The variable is not a solution.
d. 12 = n – 11
n = 23
12 = 23 – 11
12 = 12
The variable is a solution.
Thus the correct answers are options A, B, D.
Solve Addition and Subtraction Equations – Page No. 443

Solve the equation, and check the solution.
Question 1.
y − 14 = 23
y = _______
Answer: 37
Explanation:
y − 14 = 23
y = 23 + 14
y = 37
Thus the solution is 37.
Question 2.
x + 3 = 15
x = _______
Answer: 12
Explanation:
The equation is x + 3 = 15
x = 15 – 3
x = 12
The solution is 12.
Question 3.
n + \(\frac{2}{5}=\frac{4}{5}\)
n = _______ \(\frac{□}{□}\)
Answer: \(\frac{2}{5}\)
Explanation:
The equation is n + \(\frac{2}{5}=\frac{4}{5}\)
n + \(\frac{2}{5}\) = \(\frac{4}{5}\)
n = \(\frac{4}{5}\) – \(\frac{2}{5}\)
n = (4 – 2)/5
n = \(\frac{2}{5}\)
Thus the solution is \(\frac{2}{5}\)


Question 6.
s + 55 = 55
s = _______
Answer: 0
Explanation:
The equation is s + 55 = 55
s = 55 – 55
s = 0
The solution is s = 0
Question 7.
23 = x − 12
x = _______
Answer: 35
Explanation:
The given equation is 23 = x – 12
x – 12 = 23
x = 23 + 12
x = 35
The solution is x = 35.
Question 8.
p − 14 = 14
p = _______
Answer: 28
Explanation:
The given equation is p − 14 = 14
p = 14 + 14
p = 28
The solution is p = 28.
Question 9.
m − \(2 \frac{3}{4}=6 \frac{1}{2}\)
m = _______ \(\frac{□}{□}\)
Answer: 9 \(\frac{1}{4}\)
Explanation:
The given equation is m − \(2 \frac{3}{4}=6 \frac{1}{2}\)
m – 2 \(\frac{3}{4}\) = 6 \(\frac{1}{2}\)
m = 6 \(\frac{1}{2}\) + 2 \(\frac{3}{4}\)
m = 6 + 2 + \(\frac{1}{2}\) + \(\frac{3}{4}\)
m = 8 + 1 \(\frac{1}{4}\)
m = 9 \(\frac{1}{4}\)
Problem Solving
Question 10.
A recipe calls for 5 \(\frac{1}{2}\) cups of flour. Lorenzo only has 3 \(\frac{3}{4}\) cups of flour. Write and solve an equation to find the additional amount of flour Lorenzo needs to make the recipe.
Type below:
_____________
Answer: 1 \(\frac{3}{4}\)
Explanation:
A recipe calls for 5 \(\frac{1}{2}\) cups of flour.
Lorenzo only has 3 \(\frac{3}{4}\) cups of flour.
x + 3 \(\frac{3}{4}\) = 5 \(\frac{1}{2}\)
x = 5 \(\frac{1}{2}\) – 3 \(\frac{3}{4}\)
x = 1 \(\frac{3}{4}\)
Question 11.
Jan used 22.5 gallons of water in the shower. This amount is 7.5 gallons less than the amount she used for washing clothes. Write and solve an equation to find the amount of water Jan used to wash clothes.
Type below:
_____________
Answer: 30
Explanation:
Jan used 22.5 gallons of water in the shower.
This amount is 7.5 gallons less than the amount she used for washing clothes.
Let the amount of water Jan used to wash clothes be x
x – 7.5 = 22.5
x = 22.5 + 7.5
x = 30
Therefore the amount of water Jan used to wash clothes is 30 gallons.
Question 12.
Explain how to check if your solution to an equation is correct.
Type below:
_____________
Answer:
i. Evaluate the left-hand side expression at the given value to get a number.
ii. Evaluate the right-hand side expression at the given value to get a number.
iii. See if the numbers match.
Lesson Check – Page No. 444
Question 1.
The price tag on a shirt says $21.50. The final cost of the shirt, including sales tax, is $23.22. The equation 21.50 + t = 23.22 can be used to find the amount of sales tax t in dollars. What is the sales tax?
$ _______
Answer: 1.72
Explanation:
The price tag on a shirt says $21.50.
The final cost of the shirt, including sales tax, is $23.22.
The equation is 21.50 + t = 23.22
t = 23.22 – 21.50
t = 1.72
Therefore the sales tax is $1.72 dollars.

Spiral Review
Question 3.
How would you convert a mass in centigrams to a mass in milligrams?
Type below:
_____________
Answer: The conversion factor is 10; so 1 centigram = 10 milligrams. In other words, the value in cg multiplies by 10 to get a value in mg.
Question 4.
In the expression 4 + 3x + 5y, what is the coefficient of x?
The coefficient is _______
Answer:
A numerical or constant quantity placed before and multiplying the variable in an algebraic expression.
Thus the coefficient of 3x is 3.
Question 5.
Write an expression that is equivalent to 10c.
Type below:
_____________
Answer:
-2(-5c) expand the brackets
-2 × -5c
= 10c
Question 6.
Miranda bought a $7-movie ticket and popcorn for a total of $10. The equation 7 + x = 10 can be used to find the cost x in dollars of the popcorn. How much did the popcorn cost?
$ _______
Answer: 3
Explanation:
Miranda bought a $7-movie ticket and popcorn for a total of $10.
The equation is 7 + x = 10
x = 10 – 7
x = 3
Therefore the cost of the popcorn is $3.
Share and Show – Page No. 447
Model and solve the equation by using algebra tiles.
Question 1.
4x = 16
x = _______
Answer: 4
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 4x in the left rectangle, and model 16 in the right rectangle.
- There are four x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into 4 equal groups.
Question 2.
3x = 12
x = _______
Answer: 4
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 3x in the left rectangle, and model 12 in the right rectangle.
- There are three x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into 3 equal groups.
Question 3.
4 = 4x
x = _______
Answer: 1
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 4x in the left rectangle, and model 4 in the right rectangle.
- There are four x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into 4 equal groups.
Question 4.
3x = 9
x = _______
Answer: 3
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 3x in the left rectangle, and model 9 in the right rectangle.
- There are three x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into 3 equal groups.
Question 5.
2x = 10
x = _______
Answer: 5
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 2x in the left rectangle, and model 10 in the right rectangle.
- There are two x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into two equal groups.
Question 6.
15 = 5x
x = _______
Answer: 3
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 5x in the left rectangle, and model 15 in the right rectangle.
- There are five x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into five equal groups.
Solve the equation by drawing a model.
Question 7.
4x = 8
x = _______
Answer: 2
Question 8.
3x = 18
x = _______
Answer: 6

Problem Solving + Applications
Question 9.
Communicate Explain the steps you use to solve a multiplication equation with algebra tiles.
Type below:
_____________
Answer:
To solve an equation, model the terms of the equation on both sides of an equals sign.
Isolate the variable on one side by adding opposites and creating zero pairs.
To remove a factor from the variable, divide the sides into rows equal to the factor, and distribute the terms equally among all the rows.
Page No. 448
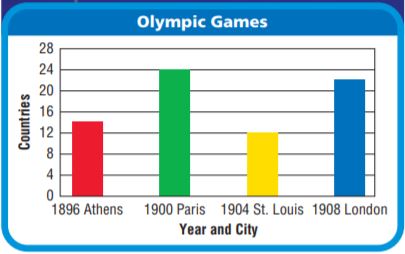
The bar graph shows the number of countries that competed in the first four modern Olympic Games. Use the bar graph for 10–11.
Question 10.
Naomi is doing a report about the 1900 and 1904 Olympic Games. Each page will contain info7rmation about 4 of the countries that competed each year. Write and solve an equation to find the number of pages Naomi will need.
_______ pages
Answer: 9 pages
Explanation:
By seeing the above table we can say that the equation is 4x = 36
The number of countries that competed in the 1900 summer Olympic games is 24.
The number of countries that competed in the 1904 summer Olympic games is 12.
The total number of countries competed in total is 36.
Each page of Naomi’s report contains information about 4 of the countries that competed each year.
4x = 36
x = 36/4
x = 9
Thus Naomi would require 9 pages to complete her report.
Question 11.
Pose a Problem Use the information in the bar graph to write and solve a problem involving a multiplication equation.
Type below:
_____________
Answer:
By seeing the above table we can say that the equation is 4x = 72
The number of countries that competed in the 1900 summer Olympic games is 24.
The number of countries that competed in the 1904 summer Olympic games is 12.
The number of countries that competed in the 1896 summer Olympic games is 14.
The number of countries that competed in the 1908 summer Olympic games is 22.
The total number of countries competed in total is 72.
4x = 72
x = 72/4
x = 18
Question 12.
The equation 7s = 21 can be used to find the number of snakes s in each cage at a zoo. Solve the equation. Then tell what the solution means.
s = _______
Answer: 3
Explanation:
The equation 7s = 21 can be used to find the number of snakes s in each cage at a zoo. Solve the equation.
7 × s = 21
s = 21/7 = 3
The solution s is 3.
Question 13.
A choir is made up of 6 vocal groups. Each group has an equal number of singers. There are 18 singers in the choir. Solve the equation 6p = 18 to find the number of singers in each group. Use a model.
_______ singers
Answer: 3 singers
Explanation:
A choir is made up of 6 vocal groups. Each group has an equal number of singers.
There are 18 singers in the choir.
The equation 6p = 18
p = 18/6 = 3
p = 3
The solution p is 3.
Model and Solve Multiplication Equations – Page No. 449
Model and solve the equation by using algebra tiles.
Question 1.
2x = 8
x = _______
Answer: 4
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 2x in the left rectangle, and model 8 in the right rectangle.
- There are two x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into two equal groups.
Question 2.
5x = 10
x = _______
Answer: 2
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 5x in the left rectangle, and model 10 in the right rectangle.
- There are five x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into five equal groups.
Question 3.
21 = 3x
x = _______
Answer: 7
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 3x in the left rectangle, and model 21 in the right rectangle.
- There are three x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into three equal groups.
Solve the equation by drawing a model.
Question 4.
6 = 3x
Answer: 2
Question 5.
4x = 12
x = _______
Answer: 3
Problem Solving
Question 6.
A chef used 20 eggs to make 5 omelets. Model and solve the equation 5x = 20 to find the number of eggs x in each omelet.
_______ eggs
Answer: 4
Explanation:
A chef used 20 eggs to make 5 omelets.
The equation is 5x = 20
x = 50/5 = 4
Thus there are 4 eggs in each omelet.
Question 7.
Last month, Julio played 3 times as many video games as Scott did. Julio played 18 video games. Write and solve an equation to find the number of video games Scott played.
_______ video games
Answer: 6
Explanation:
Last month, Julio played 3 times as many video games as Scott did. Julio played 18 video games.
The equation will be 3x = 18
x = 18/3 = 6
x = 6
The number of video games Scott played is 6.
Question 8.
Write a multiplication equation, and explain how you can solve it by using a model.
Type below:
_____________
Answer:
15 = 5x
Explanation:
- Draw 2 rectangles on your Mathboard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model 5x in the left rectangle, and model 15 in the right rectangle.
- There are five x tiles on the left side of your model. To solve the equation by using the model, you need to find the value of one x tile.
- To do this, divide each side of your model into five equal groups.
Lesson Check – Page No. 450
Question 1.
What is the solution of the equation that is modeled by the algebra tiles?
x = 1 _______
Answer: 1
Explanation:
The equation for the above figure is 3x = 3
Substitute x = 1
3(1) = 3
3/3 = 1
Thus the solution is 1.

Spiral Review
Question 3.
A rectangle is 12 feet wide and 96 inches long. What is the area of the rectangle?
_______ square feet
Answer: 1152
Explanation:
A rectangle is 12 feet wide and 96 inches long.
Area of rectangle is l × w
A = 12 × 96
A = 1152 square feet.
Thus the area of the rectangle is 1152 square feet.
Question 4.
Evaluate the algebraic expression 24 – x ÷ y for x = 8 and y = 2.
_______
Answer: 20
Explanation:
24 – x ÷ y for x = 8 and y = 2.
Substitute the value of x and y in the equation.
24 – (8 ÷ 2)
24 – 4 = 20

Question 6.
A pet store usually keeps 12 birds per cage, and there are 7 birds in the cage now. The equation 7 + x = 12 can be used to find the remaining number of birds x that can be placed in the cage. What is the solution to the equation?
x = _______
Answer: 5
Explanation:
A pet store usually keeps 12 birds per cage, and there are 7 birds in the cage now.
The equation is 7 + x = 12
x = 12 – 7
x = 5
Thus the solution of the equation is 5.
Share and Show – Page No. 453
Question 1.
Solve the equation 2.5m = 10.
m = _______
Answer: 4
Explanation:
2.5m = 10
m = 10/2.5
m = 4
Solve the equation, and check the solution.
Question 2.
3x = 210
x = _______
Answer: 70
Explanation:
3x = 210
x = 210/3
x = 70
Question 3.
2.8 = 4t
t = _______
Answer: 0.7
Explanation:
2.8 = 4t
4t = 2.8
t = 2.8/4
t = 0.7
Question 4.
\(\frac{1}{3}\)n = 15
n = _______
Answer: 45
Explanation:
\(\frac{1}{3}\)n = 15
n = 15 × 3
n = 45
Question 5.
\(\frac{1}{2}\)y = \(\frac{1}{10}\)
y = _______
Answer: \(\frac{1}{5}\)
Explanation:
\(\frac{1}{2}\)y = \(\frac{1}{10}\)
y = \(\frac{1}{10}\) × 2
y = \(\frac{1}{5}\)
Question 6.
25 = \(\frac{a}{5}\)
a = _______
Answer: 125
Explanation:
25 = \(\frac{a}{5}\)
a = 25 × 5
a = 125
Question 7.
1.3 = \(\frac{c}{4}\)
c = _______
Answer: 5.2
Explanation:
1.3 = \(\frac{c}{4}\)
c = 1.3 × 4
c = 5.2
On Your Own
Practice: Copy and Solve Solve the equation, and check the solution.
Question 8.
150 = 6m
m = _______
Answer: 25
Explanation:
6m = 150
m = 150/6
m = 25
Question 11.
There are 100 calories in 8 fluid ounces of orange juice and 140 calories in 8 fluid ounces of pineapple juice. Tia mixed 4 fluid ounces of each juice. Write and solve an equation to find the number of calories in each fluid ounce of Tia’s juice mixture.
_______ calories
Answer: 15 calories
Explanation:
Number of calories in 8 ounces of orange juice = 100
Number of calories in 1 ounce of juice = 100/8
Number of calories in 4 ounces of juice 100/8 × 4 = 50 calories
Number of calories in 8 ounces of pineapple juice = 140
Number of calories in 1 ounce of juice = 140/8
Number of calories in 4 ounces of pineapple juice = 140/8 × 4 =70 calories
Now the mixture has 50 + 70 calories = 120 calories in 8 ounces
So, 1 ounce of the mixture has 120/8 = 15 calories.
Question 12.
Write a division equation that has the solution x = 16.
Type below:
_____________
Answer:
2x = 32
x = 32/2
x = 16
Thus the equation is x = 16.
Problem Solving + Applications – Page No. 454
What’s the Error?
Question 13.
Melinda has a block of clay that weighs 14.4 ounces. She divides the clay into 6 equal pieces. To find the weight w in ounces of each piece, Melinda solved the equation 6w = 14.4.
Look at how Melinda solved the equation. Find her error.
6w = 14.4
\(\frac{6 w}{6}\) = 6 × 14.4
w = 86.4
Correct the error. Solve the equation, and explain your steps.
Describe the error that Melinda made
Type below:
_____________
Answer:
Melinda has a block of clay that weighs 14.4 ounces. She divides the clay into 6 equal pieces.
The equation is 6w = 14.4
Their error of Melinda is she used the multiplication equation to solve the equation.
She must have used the division equation to get the solution.
6w = 14.4
w = 14.4/6
w = 2.4
Question 14.
For numbers 14a−14d, choose Yes or No to indicate whether the equation has the solution x = 15.
14a. 15x = 30
14b. 4x = 60
14c. \(\frac{x}{5}\) = 3
14d. \(\frac{x}{3}\) = 5
14a. _____________
14b. _____________
14c. _____________
14d. _____________
Answer:
Given the value of x is 15
14a. 15x = 30
15 × 15 = 30
225 ≠ 30
The answer is No.
14b. 4x = 60
4 × 15 = 60
60 = 60
The answer is yes.
14c. \(\frac{x}{5}\) = 3
x/5 = 3
15/5 = 3
3 = 3
The answer is yes.
14d. \(\frac{x}{3}\) = 5
x/3 = 5
15/3 = 5
5 = 5
The answer is yes.
Solve Multiplication and Division Equations – Page No. 455
Solve the equation, and check the solution.


Question 3.
3.5x = 14.7
x = ________
Answer: 4.2
Explanation:
The given equation is
3.5x = 14.7
x = 14.7/3.5
x = 4.2
The solution x is 4.2
Question 4.
32 = 3.2c
c = ________
Answer: 10
Explanation:
The given equation is
32 = 3.2c
3.2 × c = 32
c = 32/3.2
c = 1/0.1 = 10
The solution c is 10.
Question 5.
\(\frac{2}{5}\)w = 40
w = ________
Answer: 100
Explanation:
The given equation is
\(\frac{2}{5}\)w = 40
\(\frac{2}{5}\) × w = 40
w = 40 × 5/2
w = 200/2
w = 100
Question 6.
\(\frac{a}{14}\) = 6.8
a = ________
Answer: 95.2
Explanation:
The given equation is
\(\frac{a}{14}\) = 6.8
a = 6.8 × 14
a = 95.2
Question 7.
1.6x = 1.6
x = ________
Answer: 1
Explanation:
The given equation is
1.6x = 1.6
x = 1.6/1.6
x = 1
The solution x is 1

Problem Solving
Question 10.
Anne runs 6 laps on a track. She runs a total of 1 mile, or 5,280 feet. Write and solve an equation to find the distance, in feet, that she runs in each lap.
________ feet
Answer: 880
Explanation:
Anne runs 6 laps on a track. She runs a total of 1 mile, or 5,280 feet.
Let the l represents the runs in each lap.
6 × l = 5280 feet
l = 5280/6
l = 880 feet
Therefore Anne runs 880 feets in each lap.
Question 11.
In a serving of 8 fluid ounces of pomegranate juice, there are 32.8 grams of carbohydrates. Write and solve an equation to find the amount of carbohydrates in each fluid ounce of the juice.
________ grams
Answer: 4.1
Explanation:
Given, In a serving of 8 fluid ounces of pomegranate juice, there are 32.8 grams of carbohydrates.
Let c represents the amount of carbohydrates in each fluid ounce of the juice
8 × c = 32.8 grams
c = 32.8/8
c = 4.1 grams
Question 12.
Write and solve a word problem that can be solved by solving a multiplication equation.
Type below:
_____________
Answer:
The quotient of 6 and p is 12
6 ÷ p = 12
p = 6/12
p = 1/2
Lesson Check – Page No. 456
Question 1.
Estella buys 1.8 pounds of walnuts for a total of $5.04. She solves the equation 1.8p = 5.04 to find the price p in dollars of one pound of walnuts. What does one pound of walnuts cost?
$ ________
Answer: 2.8
Explanation:
Given that, Estella buys 1.8 pounds of walnuts for a total of $5.04.
p represents the price in dollars of one pound of walnuts.
The equation to find one pound of walnuts cost is 1.8p = 5.04
1.8p = 5.04
p = 5.04/1.8
p = 2.8
Therefore the cost of one pound of walnuts is $2.8

Spiral Review
Question 3.
At top speed, a coyote can run at a speed of 44 miles per hour. If a coyote could maintain its top speed, how far could it run in 15 minutes?
________ miles
Answer: 11
Explanation:
At top speed, a coyote can run at a speed of 44 miles per hour.
Convert from minutes to hour.
60 minutes = 1 hour
15 minutes = 15 × 1/60 = 0.25 = 1/4
44 × 1/4 = 11 miles
A coyote can run at a speed of 11 miles for 15 minutes.
Question 4.
An online store sells DVDs for $10 each. The shipping charge for an entire order is $5.50. Frank orders d DVDs. Write an expression that represents the total cost of Frank’s DVDs.
Type below:
_____________
Answer: 10d + $5.50
Explanation:
An online store sells DVDs for $10 each.
The shipping charge for an entire order is $5.50. Frank orders d DVDs.
The expression will be the product of 10 and d more than 5.50
The expression is 10d + $5.50
Question 5.
A ring costs $27 more than a pair of earrings. The ring costs $90. Write an equation that can be used to find the cost c in dollars of the earrings.
Type below:
_____________
Answer: $90 – $27 = c
Explanation:
A ring costs $27 more than a pair of earrings.
The ring costs $90.
c represents the cost in dollars of the earrings.
Thus the equation is c + $27 = $90
c = $90 – $27.

Share and Show – Page No. 459
Question 1.
Connor ran 3 kilometers in a relay race. His distance represents \(\frac{3}{10}\) of the total distance of the race. The equation \(\frac{3}{10}\)d = 3 can be used to find the total distance d of the race in kilometers. What was the total distance of the race?
________ kilometers
Answer: 10
Explanation:
Connor ran 3 kilometers in a relay race.
His distance represents \(\frac{3}{10}\) of the total distance of the race.
\(\frac{3}{10}\)d = 3
3 × d = 3 × 10
3 × d = 30
d = 30/3 = 10 kilometers
Therefore the total distance of the race is 10 kilometers.

Question 3.
The lightest puppy in a litter weighs 9 ounces, which is \(\frac{3}{4}\) of the weight of the heaviest puppy. The equation \(\frac{3}{4}\)w = 9 can be used to find the weight w in ounces of the heaviest puppy. How much does the heaviest puppy weigh?
________ ounces
Answer: 12
Explanation:
The lightest puppy in a litter weighs 9 ounces, which is \(\frac{3}{4}\) of the weight of the heaviest puppy.
\(\frac{3}{4}\)w = 9
3 × w = 9 × 4
3 × w = 36
w = 36/3
w = 12
The heaviest puppy weighs 12 ounces.
Question 4.
Sophia took home \(\frac{2}{5}\) of the pizza that was left over from a party. The amount she took represents \(\frac{1}{2}\) of a whole pizza. The equation \(\frac{2}{5}\)p = \(\frac{1}{2}\) can be used to find the number of pizzas p left over from the party. How many pizzas were left over?
_______ \(\frac{□}{□}\) pizzas
Answer: 1 \(\frac{1}{4}\) pizzas
Explanation:
Sophia took home \(\frac{2}{5}\) of the pizza that was left over from a party.
The amount she took represents \(\frac{1}{2}\) of a whole pizza.
\(\frac{2}{5}\)p = \(\frac{1}{2}\)
p = \(\frac{1}{2}\) × \(\frac{5}{2}\)
p = \(\frac{5}{4}\)
p = 1 \(\frac{1}{4}\) pizzas
1 \(\frac{1}{4}\) pizzas were leftover.
Question 5.
A city received \(\frac{3}{4}\) inch of rain on July 31. This represents \(\frac{3}{10}\) of the total amount of rain the city received in July. The equation \(\frac{3}{10}\)r = \(\frac{3}{4}\) can be used to find the amount of rain r in inches the city received in July. How much rain did the city receive in July?
_______ \(\frac{□}{□}\) inches of rain
Answer: 2 \(\frac{1}{2}\) inches of rain
Explanation:
A city received \(\frac{3}{4}\) inch of rain on July 31.
This represents \(\frac{3}{10}\) of the total amount of rain the city received in July.
\(\frac{3}{10}\)r = \(\frac{3}{4}\)
r = \(\frac{3}{4}\) × \(\frac{10}{3}\)
r = \(\frac{30}{12}\)
r = \(\frac{5}{2}\)
r = 2 \(\frac{1}{2}\)
The city received 2 \(\frac{1}{2}\) inches of rain in July.
On Your Own – Page No. 460
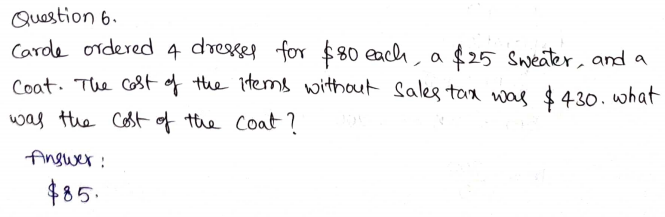

Question 7.
A dog sled race is 25 miles long. The equation \(\frac{5}{8}\)k = 25 can be used to estimate the race’s length k in kilometers. Approximately how many hours will it take a dog sled team to finish the race if it travels at an average speed of 30 kilometers per hour?
_______ \(\frac{□}{□}\) hours
Answer: 1 \(\frac{1}{3}\) hours
Explanation:
A dog sled race is 25 miles long.
The equation \(\frac{5}{8}\)k = 25
k represents race length in kilometers.
\(\frac{5}{8}\)k = 25
5 × k = 25 × 8
5k = 200
k = 200/5 = 40
k = 40
Average speed is k/30
40/30 = 4/3
The average speed of 30 kilometers per hour is 1 \(\frac{1}{3}\) hours.

Question 9.
In a basket of fruit, \(\frac{5}{6}\) of the pieces of fruit are apples. There are 20 apples in the display. The equation \(\frac{5}{6}\)f = 20 can be used to find how many pieces of fruit f are in the basket. Use words and numbers to explain how to solve the equation to find how many pieces of fruit are in the basket.
_______ pieces of fruit
Answer: 24
Explanation:
In a basket of fruit, \(\frac{5}{6}\) of the pieces of fruit are apples.
There are 20 apples in the display.
\(\frac{5}{6}\)f = 20
5 × f = 20 × 6
5 × f = 120
f = 120/5
f = 24
There are 24 pieces of friut in the basket.
Problem Solving Equations with Fractions – Page No. 461
Read each problem and solve.
Question 1.
Stu is 4 feet tall. This height represents \(\frac{6}{7}\) of his brother’s height. The equation \(\frac{6}{7}\)h = 4 can be used to find the height h, in feet, of Stu’s brother. How tall is Stu’s brother?
______ \(\frac{□}{□}\) feet
Answer: 4 \(\frac{2}{3}\) feet
Explanation:
Stu is 4 feet tall. This height represents \(\frac{6}{7}\) of his brother’s height.
The equation \(\frac{6}{7}\)h = 4
6/7 × h = 4
6 × h = 4 × 7
6 × h =28
h = 28/6
h = 14/3
h = 4 \(\frac{2}{3}\) feet
Thus the height of Stu’s brother in feet is 4 \(\frac{2}{3}\) feet.
Question 2.
Bryce bought a bag of cashews. He served \(\frac{7}{8}\) pound of cashews at a party. This amount represents \(\frac{2}{3}\) of the entire bag. The equation \(\frac{2}{3}\)n = \(\frac{7}{8}\) can be used to find the number of pounds n in a full bag. How many pounds of cashews were in the bag that Bryce bought?
______ \(\frac{□}{□}\) pounds
Answer: 1 \(\frac{5}{16}\)
Explanation:
Bryce bought a bag of cashews.
He served \(\frac{7}{8}\) pound of cashews at a party.
This amount represents \(\frac{2}{3}\) of the entire bag.
\(\frac{2}{3}\)n = \(\frac{7}{8}\)
n = \(\frac{7}{8}\) × \(\frac{3}{2}\)
n = \(\frac{21}{16}\)
n = 1 \(\frac{5}{16}\)
Bryce bought 1 \(\frac{5}{16}\) pounds of cashews were in the bag.

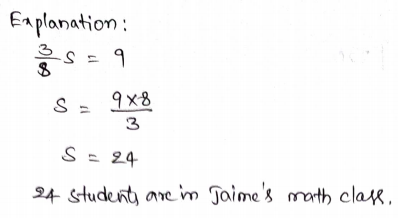

Lesson Check – Page No. 462
Question 1.
Roger served \(\frac{5}{8}\) pound of crackers, which was \(\frac{2}{3}\) of the entire box. What was the weight of the crackers originally in the box?
\(\frac{□}{□}\) pounds
Answer: \(\frac{15}{16}\) pounds
Explanation:
Roger served \(\frac{5}{8}\) pound of crackers, which was \(\frac{2}{3}\)
\(\frac{2}{3}\) × p = \(\frac{5}{8}\)
p = \(\frac{5}{8}\) × \(\frac{3}{2}\)
p = \(\frac{15}{16}\) pounds
\(\frac{15}{16}\) was the weight of the crackers originally in the box.
Question 2.
Bowser ate 4 \(\frac{1}{2}\) pounds of dog food. That amount is \(\frac{3}{4}\) of the entire bag of dog food. How many pounds of dog food were originally in the bag?
______ pounds
Answer 6 pounds
Explanation:
Bowser ate 4 \(\frac{1}{2}\) pounds of dog food.
That amount is \(\frac{3}{4}\) of the entire bag of dog food.
4 \(\frac{1}{2}\) = \(\frac{9}{2}\)
\(\frac{3}{4}\) p = \(\frac{9}{2}\)
p = \(\frac{9}{2}\) × \(\frac{4}{3}\)
p = 6 pounds
6 pounds of dog food were originally in the bag.
Spiral Review
Question 3.
What is the quotient 4 \(\frac{2}{3}\) ÷ 4 \(\frac{1}{5}\)
_______ \(\frac{□}{□}\)
Answer: 1 \(\frac{1}{9}\)
Explanation:
4 \(\frac{2}{3}\) ÷ 4 \(\frac{1}{5}\)
\(\frac{14}{3}\) ÷ \(\frac{21}{5}\)
= \(\frac{70}{63}\)
The mixed fraction of \(\frac{70}{63}\) is 1 \(\frac{1}{9}\)
4 \(\frac{2}{3}\) ÷ 4 \(\frac{1}{5}\) = 1 \(\frac{1}{9}\)
Question 4.
Miranda had 4 pounds, 6 ounces of clay. She divided it into 10 equal parts. How heavy was each part?
_______ ounces
Answer: 7 ounces
Explanation:
Miranda had 4 pounds, 6 ounces of clay.
She divided it into 10 equal parts.
Convert from pounds to ounces
We know that
1 pound = 16 ounces
4 pounds = 4 × 16 ounces = 64 ounces
64 ounces + 6 ounces = 70 ounces
Now divide 70 ounces into 10 equal parts.
70 ÷ 10 = 7 ounces.
Thus each part was 7 ounces.
Question 5.
The amount Denise charges to repair computers is $50 an hour plus a $25 service fee. Write an expression to show how much she will charge for h hours of work.
Type below:
_____________
Answer: 50h + 25
Explanation:
The amount Denise charges to repair computers is $50 an hour plus a $25 service fee.
The expression will be the product of 50 and h more than 25.
The expression is 50h + 25.

Mid-Chapter Checkpoint – Vocabulary – Page No. 463
Choose the best term from the box to complete the sentence.

Question 1.
A(n) _____ is a statement that two mathematical expressions are equal.
Type below:
_____________
Answer: An equation is a mathematical statement that two expressions are equal.
Question 2.
Adding 5 and subtracting 5 are _____.
Type below:
_____________
Answer: Solution of an equation.
Concepts and Skills
Write an equation for the word sentence.
Question 3.
The sum of a number and 4.5 is 8.2.
Type below:
_____________
Answer:
The phrase “sum” indicates an addition operation.
So, the equation is n + 4.5 = 8.2
Question 4.
Three times the cost is $24.
Type below:
_____________
Answer:
The phrase “times” indicates multiplication.
Multiply 3 with c.
3c = 24
Determine whether the given value of the variable is a solution of the equation.


Solve the equation, and check the solution.
Question 7.
a + 2.4 = 7.8
a = _____
Answer: 5.4
Explanation:
Given the equation is a + 2.4 = 7.8
a + 2.4 = 7.8
a = 7.8 – 2.4
a = 5.4
Question 8.
\(b-\frac{1}{4}=3 \frac{1}{2}\)
b = _______ \(\frac{□}{□}\)
Answer: 3 \(\frac{3}{4}\)
Explanation:
Given the equation is \(b-\frac{1}{4}=3 \frac{1}{2}\)
b – \(\frac{1}{4}\) = 3 \(\frac{1}{2}\)
b = 3 \(\frac{1}{2}\) + \(\frac{1}{4}\)
b = 3 + \(\frac{1}{4}\) + \(\frac{1}{2}\)
b = 3 \(\frac{3}{4}\)
Question 9.
3x = 27
x = _______
Answer: 9
Explanation:
Given the equation is 3x = 27
x = 27/3
x = 9
Question 10.
\(\frac{1}{3} s=\frac{1}{5}\)
s = \(\frac{□}{□}\)
Answer: \(\frac{3}{5}\)
Explanation:
Given the equation is \(\frac{1}{3} s=\frac{1}{5}\)
\(\frac{1}{3}\)s = \(\frac{1}{5}\)
s = \(\frac{3}{5}\)
Question 11.
\(\frac{t}{4}\) = 16
t = _______
Answer: 64
Explanation:
Given the equation is \(\frac{t}{4}\) = 16
t = 16 × 4
t = 64
Question 12.
\(\frac{w}{7}\) = 0.3
w = _______
Answer: 2.1
Explanation:
\(\frac{w}{7}\) = 0.3
w/7 = 0.3
w = 0.3 × 7
w = 2.1
Page No. 464
Question 13.
A stadium has a total of 18,000 seats. Of these, 7,500 are field seats, and the rest are grandstand seats. Write an equation that could be used to find the number of grandstand seats s.
Type below:
_____________
Answer: s + 7500 = 18000
Explanation:
A stadium has a total of 18,000 seats.
Of these, 7,500 are field seats, and the rest are grandstand seats.
Let s be the number of grandstand seats.
s + 7,500 = 18,000
Question 14.
Aaron wants to buy a bicycle that costs $128. So far, he has saved $56. The equation a + 56 = 128 can be used to find the amount a in dollars that Aaron still needs to save. What is the solution of the equation?
The solution is _______
Answer: 72
Explanation:
Aaron wants to buy a bicycle that costs $128. So far, he has saved $56.
The equation a + 56 = 128
a = 128 – 56
a = 72
The solution of the equation a + 56 = 128 is 72.

Question 16.
Crystal is picking blueberries. So far, she has filled \(\frac{2}{3}\) of her basket, and the blueberries weigh \(\frac{3}{4}\) pound. The equation \(\frac{2}{3}\)w = \(\frac{3}{4}\) can be used to estimate the weight w in pounds of the blueberries when the basket is full. About how much will the blueberries in Crystal’s basket weigh when it is full?
______ \(\frac{□}{□}\) pounds
Answer: 1 \(\frac{1}{8}\) pounds
Explanation:
Crystal is picking blueberries. So far, she has filled \(\frac{2}{3}\) of her basket, and the blueberries weigh \(\frac{3}{4}\) pound.
The equation \(\frac{2}{3}\)w = \(\frac{3}{4}\)
w = \(\frac{3}{4}\) × \(\frac{3}{2}\)
w = \(\frac{9}{8}\)
The mixed fraction of \(\frac{9}{8}\) is 1 \(\frac{1}{8}\) pounds
Share and Show – Page No. 467
Determine whether the given value of the variable is a solution of the inequality.
Question 1.
a ≥ −6, a = −3
The variable is _____________
Answer: a solution
Explanation:
Substitute the solution a in the inequality.
a = -3
-3 ≥ -6
-3 is greater than -6
Thus the variable is a solution.
Question 2.
y < 7.8, y = 8 The variable is _____________
Answer: not a solution
Explanation:
Substitute the solution y in the inequality.
y = 8
8 is less than 7.8
8<7.8
The variable is not the solution.
Question 3.
c > \(\frac{1}{4}\), c = \(\frac{1}{5}\)
The variable is _____________
Answer: not a solution
Explanation:
Substitute the solution c in the inequality.
c = \(\frac{1}{5}\)
\(\frac{1}{5}\) > \(\frac{1}{4}\)
\(\frac{1}{5}\) is greater than \(\frac{1}{4}\)
\(\frac{1}{5}\) > \(\frac{1}{4}\)
Thus the variable is a solution.
Question 4.
x ≤ 3, x = 3
The variable is _____________
Answer: a solution
Explanation:
Substitute the solution x in the inequality.
x = 3
3 ≤ 3
3 is less than or equal to 3.
Thus the variable is a solution.
Question 5.
d < –0.52, d = –0.51
The variable is _____________
Answer: not a solution
Explanation:
Substitute the solution d in the inequality.
-0.51 < -0.52
-0.51 is greater than -0.52
The variable is not the solution.
Question 6.
t ≥ \(\frac{2}{3}\), t = \(\frac{3}{4}\)
The variable is _____________
Answer: a solution
Explanation:
Substitute the solution t in the inequality.
t = \(\frac{3}{4}\)
\(\frac{3}{4}\) ≥ \(\frac{2}{3}\)
\(\frac{3}{4}\) is greater than \(\frac{2}{3}\)
Thus the variable is a solution.
On Your Own
Practice: Copy and Solve Determine whether s = \(\frac{3}{5}\), s = 0, or s = 1.75 are solutions of the inequality.
Question 7.
s > –1
Type below:
_____________
Answer:
s > –1
s = \(\frac{3}{5}\)
\(\frac{3}{5}\) > -1
\(\frac{3}{5}\) is greater than -1.
The variable is the solution.
s = 0
0 > -1
0 is greater than -1
Thus the variable is a solution.
s = 1.75
1.75 > -1
1.75 is greater than -1
s > -1
Thus the variable is a solution.
Question 8.
s ≤ 1 \(\frac{2}{3}\)
Type below:
_____________
Answer:
s ≤ 1 \(\frac{2}{3}\)
s = \(\frac{3}{5}\)
\(\frac{3}{5}\) ≤ 1 \(\frac{2}{3}\)
\(\frac{3}{5}\) is less than but not equal to 1 \(\frac{2}{3}\)
The variable is not the solution.
s ≤ 1 \(\frac{2}{3}\)
s = 0
0 ≤ 1 \(\frac{2}{3}\)
The variable is not the solution.
s = 1.75
1.75 ≤ 1 \(\frac{2}{3}\)
The variable is not the solution.
Question 9.
s < 0.43
Type below:
_____________
Answer:
s < 0.43
\(\frac{3}{5}\) < 0.43
\(\frac{3}{5}\) = 0.6
0.6 is not less than 0.43
Thus the variable is not the solution.
s = 0
0 < 0.43
0 is less than 0.43
Thus the variable is the solution.
s = 1.75
1.75 < 0.43
1.75 is greater than 0.43
Thus the variable is not the solution.
Give two solutions of the inequality.
Question 10.
e < 3
Type below: _____________
Answer:
The solution to the inequality must be whole numbers less than 3.
e = 1 and 2 are the solutions because 1 and 2 are less than 3.
Thus the 2 solutions are 1 and 2.
Question 11.
p > –12
Type below:
_____________
Answer:
The solution to the inequality must be whole numbers greater than -12
p = 0 and -5 are the solutions because 0 and -5 are greater than -12.
Thus the 2 solutions are 0 and -5.
Question 12.
y ≥ 5.8
Type below:
_____________
Answer:
The solution to the inequality must be whole numbers greater than or equal to 5.8
y = 5.8 and 5.9 are the solutions because 5.8 and 5.9 greater than or equal to 5.8
Thus the 2 solutions are 5.8 and 5.9
Question 13.
Connect Symbols and Words A person must be at least 18 years old to vote. The inequality a ≥ 18 represents the possible ages a in years at which a person can vote. Determine whether a = 18, a = 17\(\frac{1}{2}\), and a = 91.5 are solutions of the inequality, and tell what the solutions mean.
Type below:
_____________
Answer:
a ≥ 18
Substitute the values of a in the inequality
a = 18
18 ≥ 18
Thus the variable is the solution.
a = 17\(\frac{1}{2}\)
17\(\frac{1}{2}\) ≥ 18
17\(\frac{1}{2}\) is less than 18.
The variable is not the solution.
a = 91.5
91.5 > 18
The solution is mean.
Problem Solving + Applcations – Page No. 468
The table shows ticket and popcorn prices at five movie theater chains. Use the table for 14–15.
Question 14.
The inequality p < 4.75 represents the prices p in dollars that Paige is willing to pay for popcorn. The inequality p < 8.00 represents the prices p in dollars that Paige is willing to pay for a movie ticket. At how many theaters would Paige be willing to buy a ticket and popcorn? ______ theater
Answer: 1
Explanation:
The inequality p < 4.75 represents the prices p in dollars that Paige is willing to pay for popcorn. The inequality p < 8.00 represents the prices p in dollars that Paige is willing to pay for a movie ticket.
From the above table, we can see that there is the only theatre with 8.00 and 4.75
So, Paige is willing to buy a ticket and popcorn from 1 theatre.
Question 15.
Sense or Nonsense? Edward says that inequality d ≥ 4.00 represents the popcorn prices in the table, where d is the price of popcorn in dollars. Is Edward’s statement sense or nonsense? Explain. Type below: _____________
Answer: Edward’s statement makes sense because all of the popcorn prices in the table are greater than or equal to $4.00.
Question 16.
Use Math Vocabulary Explain why the statement t > 13 is an inequality.
Type below:
_____________
Answer: The statement is equality because it compares two amounts t and 13 using an inequality symbol.
Question 17.
The minimum wind speed for a storm to be considered a hurricane is 74 miles per hour. The inequality w ≥ 74 represents the possible wind speeds of a hurricane.
Two possible solutions for the inequality w ≥ 74 are _____ and _____.
Two possible solutions for the inequality w ≥ 74 are _____ and _____
Answer: 75 and 80
Explanation:
Given that w is greater than or equal to 74.
The two possible solutions for the inequality w ≥ 74 are 75 and 80.
Solutions of Inequalities – Page No. 469
Determine whether the given value of the variable is a solution of the inequality.
Question 1.
s ≥ –1, s = 1
The variable is _____________
Answer: a solution
Explanation:
The inequality is s ≥ –1
s = 1
1 ≥ –1
1 is a positive number so 1 will be greater than or equal to -1
Thus the variable is a solution.


Question 4.
u > \(\frac{-1}{2}\), u = 0
The variable is _____________
Answer: a solution
Explanation:
The inequality is u > \(\frac{-1}{2}\)
u = 0
0 > \(\frac{-1}{2}\)
0 is greater than \(\frac{-1}{2}\)
Thus the variable is a solution.
Question 5.
q ≥ 0.6, q = 0.23
The variable is _____________
Answer: not a solution
Explanation:
The inequality is q ≥ 0.6
q = 0.23
0.23 is less than 0.6
Thus the variable is a solution.
Question 6.
b < 2 \(\frac{3}{4}\), b = \(\frac{2}{3}\)
The variable is _____________
Answer: a solution
Explanation:
The inequality is b < 2 \(\frac{3}{4}\)
b = \(\frac{2}{3}\)
\(\frac{2}{3}\) < 2 \(\frac{3}{4}\)
\(\frac{2}{3}\) is less than 2 \(\frac{3}{4}\)
Thus the variable is a solution.
Give two solutions of the inequality.
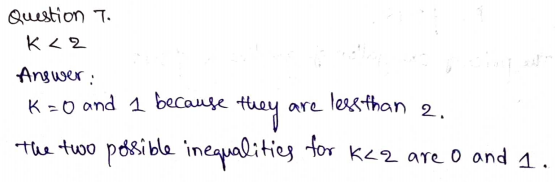
Question 8.
z ≥ –3
Type below:
_____________
Answer:
z = -3 and -2 because -3 and -2 are greater than or equal to -3
Thus the two solutions of the inequality are -3 and -2
Question 9.
f ≤ –5
Type below:
_____________
Answer:
f = -5 and -6 because -5 and -6 are less than or equal to -5
Thus the two solutions of the inequality are -5 and -6.
Problem Solving
Question 10.
The inequality s ≥ 92 represents the score s that Jared must earn on his next test to get an A on his report card. Give two possible scores that Jared could earn to get the A.
Type below:
_____________
Answer: Two possible scores that Jared could earn to get the A are 92 and 100.
Question 11.
The inequality m ≤ $20 represents the amount of money that Sheila is allowed to spend on a new hat. Give two possible money amounts that Sheila could spend on the hat.
Type below:
_____________
Answer: Two possible money amounts that Sheilla could spend on the hat are $15 or $10.
Question 12.
Describe a situation and write an inequality to represent the situation. Give a number that is a solution and another number that is not a solution of the inequality.
Type below:
_____________
Answer:
In the United States, the minimum age required to run for president is 35. This can be represented by the inequality a ≥ 35.
A number that is a solution is 55 and a number that is not a solution is 29.
Lesson Check – Page No. 470
Question 1.
Three of the following are solutions of g < –1\(\frac{1}{2}\). Which one is not a solution?
g = –4 g = –7\(\frac{1}{2}\) g = 0 g = –2\(\frac{1}{2}\)
Type below:
_____________
Answer: g = 0
Explanation:
g < –1\(\frac{1}{2}\).
g = –4
-4 < –1\(\frac{1}{2}\)
g = –7\(\frac{1}{2}\)
–7\(\frac{1}{2}\) < –1\(\frac{1}{2}\).
g = –2\(\frac{1}{2}\)
–2\(\frac{1}{2}\) < –1\(\frac{1}{2}\)
g = 0
0 < –1\(\frac{1}{2}\)
Thus 0 is not the solution.
Question 2.
The inequality w ≥ 3.2 represents the weight of each pumpkin, in pounds, that is allowed to be picked to be sold. The weights of pumpkins are listed. How many pumpkins can be sold? Which pumpkins can be sold?
3.18 lb, 4 lb, 3.2 lb, 3.4 lb, 3.15 lb
Type below:
_____________
Answer: 3.2 lb, 3.4 lb
Explanation:
The inequality w ≥ 3.2 represents the weight of each pumpkin, in pounds, that is allowed to be picked to be sold.
Substitute the solutions in the inequality.
w = 3.18
3.18 ≥ 3.2
3.18 is less than 3.2
3.18 < 3.2 lb
w = 4 lb
4 ≥ 3.2
4 is greater than 3.2
4 > 3.2
w = 3.2 lb
3.2 ≥ 3.2
3.2 lb is greater than 3.2 lb
w = 3.4 lb
3.4 ≥ 3.2
3.4 lb is greater than 3.2 lb
w = 3.15 lb
3.15 < 3.2
Thus 3.2 lb, 3.4 lb pumpkins can be sold.
Spiral Review

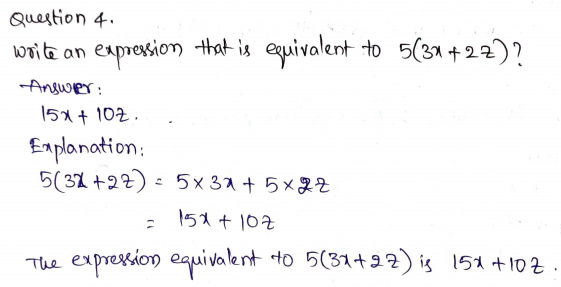
Question 5.
Tina bought a t-shirt and sandals. The total cost was $41.50. The t-shirt cost $8.95. The equation 8.95 + c = 41.50 can be used to find the cost c in dollars of the sandals. How much did the sandals cost?
$ _______
Answer: $32.55
Explanation:
Tina bought a t-shirt and sandals. The total cost was $41.50. The t-shirt cost $8.95.
The equation is 8.95 + c = 41.50
c = 41.50 – 8.95
c = $32.55
The cost of the sandal is 32.55
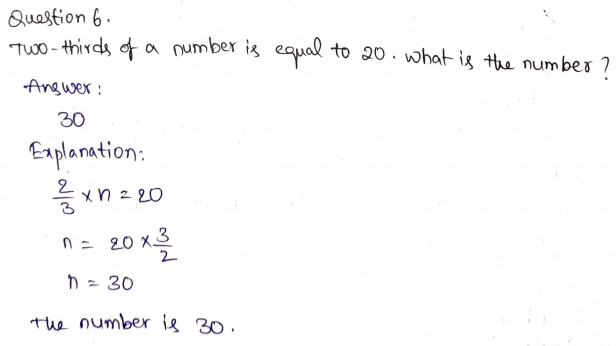
Share and Show – Page No. 473
Write an inequality for the word sentence. Tell what type of numbers the variable in the inequality can represent.
Question 1.
The elevation e is greater than or equal to 15 meters.
Type below:
_____________
Answer:
The phrase greater than or equal to represents “≥”
Thus the inequality is e ≥ 15
Question 2.
A passenger’s age a must be more than 4 years.
Type below:
_____________
Answer:
The phrase more than represents the greater than symbol “>”
Thus the inequality is a > 4
Write a word sentence for the inequality.
Question 3.
b < \(\frac{1}{2}\)
Type below:
_____________
Answer:
By seeing the above inequality we can write the word sentence for inequality as,
b is less than \(\frac{1}{2}\)
Question 4.
m ≥ 55
Type below:
_____________
Answer:
By seeing the above inequality we can write the word sentence for inequality as,
m is greater than or equal to 55.
On Your Own
Question 5.
Compare Explain the difference between t ≤ 4 and t < 4.
Type below:
_____________
Answer:
t ≤ 4 is t is less than or equal to 4 which means t is equal to 4 or 3.9.
t < 4 is t is less than 4 which means t is equal to 3, 2, or 1 or 0.
Question 6.
A children’s roller coaster is limited to riders whose height is at least 30 inches and at most 48 inches. Write two inequalities that represent the height h of riders for the roller coaster.
Type below:
_____________
Answer:
h represents the height of riders for the roller coaster.
A children’s roller coaster is limited to riders whose height is at least 30 inches and at most 48 inches.
ar least 30 inches means h must be greater than or equal to 30 inches.
i.e., h ≥ 30 inches
at most 48 inches means h must be less than 48 inches.
i.e., h < 48 inches
Question 7.
Match the inequality with the word sentence it represents.

Type below:
_____________
Answer:

Make Generalizations – Page No. 474
The reading skill make generalizations can help you write inequalities to represent situations. A generalization is a statement that is true about a group of facts.
Sea otters spend almost their entire lives in the ocean. Their thick fur helps them to stay warm in cold water. Sea otters often float together in groups called rafts. A team of biologists weighed the female sea otters in one raft off the coast of Alaska. The chart shows their results.
Question 8.
Write two inequalities that represent generalizations about the sea otter weights.
Type below:
_____________
Answer:
First, list the weights in pounds in order from least to greatest.
50, 51, 54, 58, 61, 61, 62, 62, 66, 68, 69, 71
Next, write an inequality to describe the weights by using the least weight on the list. Let w represent weights of the otters in the pounds.
The least weight is 50 pounds, so all of the weights are greater than or equal to 50 pounds.
w ≥ 50
Now write an inequality to describe the weights by using the greatest weights in the list.
The greatest weight is 71 pounds, so all of the weights are less than or equal to 71 pounds.
w ≤ 71
Question 9.
Use the chart at the right to write two inequalities that represent generalizations about the number of sea otter pups per raft.
Type below:
_____________
Answer:
First, list the number of pups in order from least to greatest.
6, 6, 7, 10, 15, 16, 20, 23
Next, write an inequality to describe the number of pups by using the least number of pups on the list. Let n represent the number of pups.
The least weight is 6 pups. So all of the pups will be greater than or equal to 6.
n ≥ 6
Now write an inequality to describe the number of pups by using the greatest weights in the list.
The greatest weight is 23 pups so all of the weights are less than or equal to 23 pups.
n ≤ 23 pups
Write Inequalities – Page No. 475
Write an inequality for the word sentence. Tell what type of numbers the variable in the inequality can represent.
Question 1.
The width w is greater than 4 centimeters.
Type below:
_____________
Answer:
The inequality symbol for “greater than” is >. w > 4, where w is the width in centimeters. w is a positive number.
Question 2.
The score s in a basketball game is greater than or equal to 10 points
Type below:
_____________
Answer:
The inequality symbol for “greater than or equal to” is ≥. s ≥ 10, where s is the score in the basketball game. s is a positive number.
Question 3.
The mass m is less than 5 kilograms
Type below:
_____________
Answer:
The inequality symbol for “less than” is <. m < 5, where m is the mass in kilograms. m is a positive number.
Question 4.
The height h is greater than 2.5 meters
Type below:
_____________
Answer:
The inequality symbol for “greater than” is >. h > 2.5, where h is the height in meters. h is a positive number.
Question 5.
The temperature t is less than or equal to −3°.
Type below:
_____________
Answer:
The inequality symbol for “less than or equal to” is ≤. t ≤ −3° where t is the temperature in degrees. t is a negative number.
Write a word sentence for the inequality.
Question 6.4
k < –7
Type below:
_____________
Answer: The word sentence for the inequality is k is less than -7.
Question 7.
z ≥ 2 \(\frac{3}{5}\)
Type below:
_____________
Answer: The word sentence for the inequality is z is greater than or equal to 2 \(\frac{3}{5}\).
Problem Solving
Question 8.
Tabby’s mom says that she must read for at least 30 minutes each night. If m represents the number of minutes reading, what inequality can represent this situation?
Type below:
_____________
Answer: m ≥ 30
Explanation:
Tabby’s mom says that she must read for at least 30 minutes each night.
m represents the number of minutes of reading.
m is greater than or equal to 30.
Thus the inequality is m ≥ 30.
Question 9.
Phillip has a $25 gift card to his favorite restaurant. He wants to use the gift card to buy lunch. If c represents the cost of his lunch, what inequality can describe all of the possible amounts of money, in dollars, that Phillip can spend on lunch?
Type below:
_____________
Answer: c ≤ 25
Explanation:
Phillip has a $25 gift card to his favorite restaurant.
He wants to use the gift card to buy lunch.
c represents the cost of his lunch
c is less than or equal to 25.
Thus the inequality is c ≤ 25.
Question 10.
Write a short paragraph explaining to a new student how to write an inequality.
Type below:
_____________
Answer:
Inequality is a statement that two quantities are not equal.
To know which direction to shade a graph, I write inequalities with the variable on the left side of the inequality symbol. I know that the symbol has to point to the same number after I rewrite the inequality.
For example, I write 4 < y as y > 4
Now the inequality symbol points in the direction in that I should draw the shaded arrow on my graph.
Lesson Check – Page No. 476
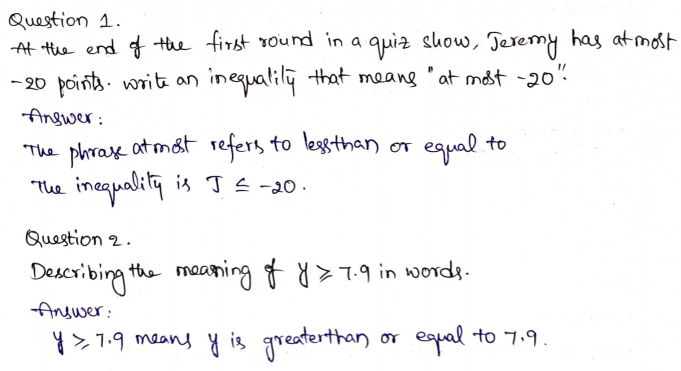
Question 2.
Describe the meaning of y ≥ 7.9 in words.
Type below:
_____________
Answer: y ≥ 7.9 means y is greater than or equal to 7.9
Spiral Review
Question 3.
Let y represent Jaron’s age in years. If Dawn were 5 years older, she would be Jaron’s age. Which expression represents Dawn’s age?
Type below:
_____________
Answer: y – 5
Explanation:
Let y represent Jaron’s age in years.
If Dawn were 5 years older, she would be Jaron’s age.
We have to subtract 5 years to know the age of Jaron.
Thus the expression is y – 5.
Question 4.
Simplify the expression 7 × 3g.
Type below:
_____________
Answer: 21g
Question 5.
What is the solution of the equation 8 = 8f?
f = ________
Answer:
8 = 8f
f = 8/8 = 1
f = 1
The solution for the equation 8 = 8f is 1.
Question 6.
Which of the following are solutions of the inequality k ≤ –2?
k = 0 k = –2 k = –4 k = 1 k = –1 \(\frac{1}{2}\)
Type below:
_____________
Answer: k = -2 k = -4
Explanation:
k = 0 in the inequality
k ≤ –2
0 ≤ –2
0 is less than but not equal to -2
Thus 0 is not the solution.
k = –2
k ≤ –2
-2 ≤ –2
Thus -2 is the solution.
k = –4
k ≤ –2
-4 ≤ –2
Thus -4 is the solution.
k = 1
1 ≤ –2
1 ≤ –2
1 is greater than but not equal to -2
Thus 1 is not the solution.
k = –1 \(\frac{1}{2}\)
–1 \(\frac{1}{2}\) ≤ –2
–1 \(\frac{1}{2}\) ≤ –2
–1 \(\frac{1}{2}\) is less than but not equal to -2
Thus –1 \(\frac{1}{2}\) is not the solution.
Share and Show – Page No. 479
Graph the inequality.
Question 1.
m < 15
Type below:
_____________
Answer:

Question 2.
c ≥ –1.5
Type below:
_____________
Answer:

Question 3.
b ≤ \(\frac{5}{8}\)
Type below:
_____________
Answer:

On Your Own
Practice: Copy and Solve Graph the inequality.
Question 4.
a < \(\frac{2}{3}\)
Type below:
_____________
Answer:

Question 5.
x > –4
Type below:
_____________
Answer:

Question 6.
k ≥ 0.3
Type below:
_____________
Answer:

Question 7.
t ≤ 6
Type below:
_____________
Answer:

Write the inequality represented by the graph.
Question 8.

Type below:
_____________
Answer: m < 6
Question 9.

Type below:
_____________
Answer: n ≥ -7
Question 10.
Model Mathematics The inequality w ≥ 60 represents the wind speed w in miles per hour of a tornado. Graph the solutions of the inequality on the number line.
Type below:
_____________
Answer:

Question 11.
Graph the solutions of the inequality c < 12 ÷ 3 on the number line
Type below:
_____________
Answer:
c < 12 ÷ 3
c < 4

Problem Solving + Applications – Page No. 480
The table shows the height requirements for rides at an amusement park. Use the table for 12–16
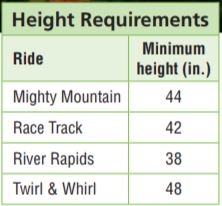
Question 12.
Write an inequality representing t, the heights in inches of people who can go on Twirl & Whirl.
Type below:
_____________
Answer:
The minimum height of people who can go on Twirl and Whirl is 48 inches.
So, inequality is t ≥ 48.
Question 13.
Graph your inequality from Exercise 12.
Type below:
_____________
Answer:
Draw a full circle at 48 to show that 48 is a solution.
Shade to the right of 48 to show that values greater than or equal to 48 are solutions.
Question 14.
Write an inequality representing r, the heights in inches of people who can go on Race Track.
Type below:
_____________
Answer:
The minimum height of people who can go on Race track is 24 inches.
So, the inequality is r ≥ 42.
Question 15.
Graph your inequality from Exercise 14.
Type below:
_____________
Answer:
Draw a full circle at 42 to show that 42 is a solution.
Shade to the right of 42 to show that values greater than or equal to 48 are solutions.
Question 16.
Write an inequality representing b, the heights in inches of people who can go on both River Rapids and Mighty Mountain. Explain how you determined your answer.
Type below:
_____________
Answer:
You need to be at least 38 inches tall to go on River Rapids and at least 44 inches tall to go on Mighty mountain.
So, you need to be at least 44 inches tall to go on both rides.
The inequality is b ≥ 44.
Question 17.
Alena graphed the inequality c ≤ 25. Darius said that 25 is not part of the solution of the inequality. Do you agree or disagree with Darius? Use numbers and words to support your answer
![]()
Type below:
_____________
Answer: Yes I agree with Darius.
That dark circle and the arrow to the left indicates that c ≤ 25
Graph Inequalities – Page No. 481
Graph the inequality.
Question 1.
h ≥ 3
Type below:
_____________
Answer:
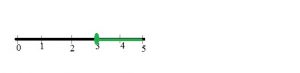
Question 2.
x < \(\frac{-4}{5}\)
Type below:
_____________
Answer:
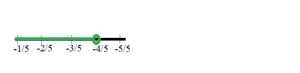
Question 3.
y > –2
Type below:
_____________
Answer:
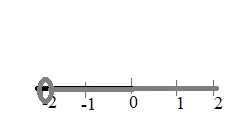
Question 4.
n ≥ 1 \(\frac{1}{2}\)
Type below:
_____________
Answer:
Question 5.
c ≤ –0.4
Type below:
_____________
Answer:

Write the inequality represented by the graph.
Question 6.

Type below:
_____________
Answer: n > 3
Question 7.
Type below:
_____________
Answer: n > -5
Problem Solving
Question 8.
The inequality x ≤ 2 represents the elevation x of a certain object found at a dig site. Graph the solutions of the inequality on the number line.
Type below:
_____________
Answer:
The inequality x ≤ 2 represents the elevation x of a certain object found at a dig site.
Question 9.
The inequality x ≥ 144 represents the possible scores x needed to pass a certain test. Graph the solutions of the inequality on the number line.
Type below:
_____________
Answer:
Question 10.
Write an inequality and graph the solutions on a number line.
Type below:
_____________
Answer:
The inequality is n ≥ -7

Lesson Check – Page No. 482
Question 1.
Write the inequality that is shown by the graph.

Type below:
_____________
Answer: x ≥ -2
The number line at right shows the solutions of the inequality x ≥ -2
Question 2.
Describe the graph of g < 0.6.
Type below:
_____________
Answer:
Spiral Review
Question 3.
Write an expression that shows the product of 5 and the difference of 12 and 9.
Type below:
_____________
Answer:
The equation for the product of 5 and the difference of 12 and 9
5 × 12 – 9
The equation is 5(12 – 9).

Question 5.
The equation 12x = 96 gives the number of egg cartons x needed to package 96 eggs. Solve the equation to find the number of cartons needed.
________ cartons
Answer: 8
Explanation:
Given,
The equation 12x = 96 gives the number of egg cartons x needed to package 96 eggs.
12x = 96
x = 96/12 = 8
Thus 8 number of cartons are needed.
Question 6.
The lowest price on an MP3 song is $0.35. Write an inequality that represents the cost c of an MP3 song.
Type below:
_____________
Answer:
Given that,
The lowest price on an MP3 song is $0.35.
c ≥ 0.35
That is an inequality to represent the cost of an MP3 song.
Chapter 8 Review/Test – Page No. 483
Question 1.
For numbers 1a–1c, choose Yes or No to indicate whether the given value of the variable is a solution of the equation.
1a. \(\frac{2}{5}\)v=10; v = 25
1b. n + 5 = 15; n = 5
1c. 5z = 25; z = 5
1a. _____________
1b. _____________
1c. _____________
Answer:
1a. \(\frac{2}{5}\)v=10; v = 25
\(\frac{2}{5}\) × 25=10
2 × 5 = 10
10 = 10
The variable is a solution.
Thus the answer is yes.
1b. n + 5 = 15; n = 5
Substitute n = 5
5 + 5 = 15
10 ≠ 15
The variable is not a solution.
The answer is no.
1c. 5z = 25; z = 5
Substitute z = 5
5 × 5 = 25
25 = 25
The variable is a solution.
Thus the answer is yes.
Question 2.
The distance from third base to home plate is 88.9 feet. Romeo was 22.1 feet away from third base when he was tagged out. The equation 88.9 − t = 22.1 can be used to determine how far he needed to run to get to home plate. Using substitution, the coach determines that Romeo needed to run _____ feet to get to home plate.
Using substitution, the coach determines that Romeo needed to run _____________ feet to get to home plate
Answer: 66.8 feet
Explanation:
The distance from third base to home plate is 88.9 feet.
Romeo was 22.1 feet away from third base when he was tagged out.
The equation is 88.9 − t = 22.1
88.9 − t = 22.1
88.9 – 22.1 = t
t = 66.8 feet
Thus Using substitution, the coach determines that Romeo needed to run 66.8 feet to get to the home plate.
Question 3.
There are 84 grapes in a bag. Four friends are sharing the grapes. Write an equation that can be used to find out how many grapes g each friend will get if each friend gets the same number of grapes.
Type below:
_____________
Answer:
84 = 4g
84 is the total amount of grapes
4 is the number of friends
g = how many grapes each friend will get
Question 4.
Match each scenario with the equation that can be used to solve it.

Type below:
_____________
Answer:
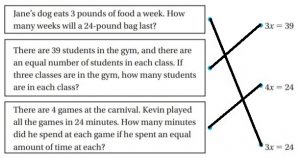
Chapter 8 Review/Test Page No. 484
Question 5.
Frank’s hockey team attempted 15 more goals than Spencer’s team. Frank’s team attempted 23 goals. Write and solve an equation that can be used to find how many goals Spencer’s team attempted.
______ goals
Answer: 8 goals
Explanation:
Frank’s hockey team attempted 15 more goals than Spencer’s team.
Frank’s team attempted 23 goals.
Let x be the Spencer’s team
The phrase more than indicates addition operation.
x + 15 = 23
x = 23 – 15
x = 8 goals
Question 6.
Ryan solved the equation 10 + y = 17 by drawing a model. Use numbers and words to explain how Ryan’s model can be used to find the solution
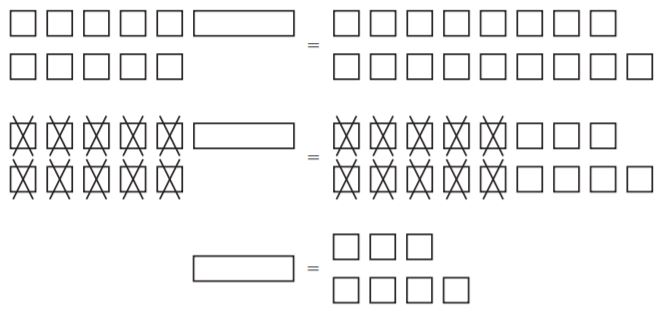
Type below:
_____________
Answer: y = 7
Explanation:
- Draw 11 rectangles on your MathBoard to represent the two sides of the equation.
- Use algebra tiles to model the equation. Model y + 10 in the left rectangle, and model 17 in the right rectangle.
- To solve the equation, get the y tile by itself on one side. If you remove a tile from one side, you can keep the two sides equal by removing the same type of tile from the other side.
- Remove ten 1 tiles on the left side and ten 1 tiles on the right side.
- The remaining titles will be seven 1 tiles on the right sides.
Thus 10 + y = 17
y = 17 – 10 = 7
y = 7

Question 8.
Select the equations that have the solution m = 17. Mark all that apply.
Options:
a. 3 + m = 21
b. m − 2 = 15
c. 14 = m − 3
d. 2 = m − 15
Answer: B, C, D
Explanation:
a. 3 + m = 21
3 + 17 = 21
20 ≠ 21
b. m − 2 = 15
17 – 2 = 15
15 = 15
c. 14 = m − 3
14 = 17 – 3
14 = 14
d. 2 = m − 15
2 = 17 – 15
2 = 2
Thus the correct answers are B, C and D.
Chapter 8 Review/Test Page No. 485
Question 9.
Describe how you could use algebra tiles to model the equation 4x = 20.
Type below:
_____________
Answer:
4x = 20
x = 20/4 = 5
x = 5
Question 10.
For numbers 10a–10d, choose Yes or No to indicate whether the equation has the solution x = 12.
10a. \(\frac{3}{4}\)x = 9
10b. 3x = 36
10c. 5x = 70
10d. \(\frac{x}{3}\) = 4
10a. _____________
10b. _____________
10c. _____________
10d. _____________
Answer:
10a. Yes
10b. Yes
10c. No
10d. Yes
Explanation:
10a. \(\frac{3}{4}\)x = 9
\(\frac{3}{4}\) × 12 = 9
3 × 3 = 9
9 = 9
Thus the answer is yes.
10b. 3x = 36
x = 12
3 × 12 = 36
36 = 36
Thus the answer is yes.
10c. 5x = 70
x = 12
5 × 12 = 70
60 ≠ 70
Thus the answer is no.
10d. \(\frac{x}{3}\) = 4
x/3 = 4
x = 4 × 3
x = 12
Thus the answer is yes.
Question 11.
Bryan rides the bus to and from work on the days he works at the library. In one month, he rode the bus 24 times. Solve the equation 2x = 24 to find the number of days Bryan worked at the library. Use a model.
Type below:
_____________
Answer:
2x = 24
x = 24/2 = 12
Thus x = 12

Chapter 8 Review/Test – Page No. 486
Question 12.
Betty needs \(\frac{3}{4}\) of a yard of fabric to make a skirt. She bought 9 yards of fabric.
Part A
Write and solve an equation to find how many skirts x she can make from 9 yards of fabric.
________ skirts
Answer: 12 skirts
Explanation:
Betty needs \(\frac{3}{4}\) of a yard of fabric to make a skirt.
She bought 9 yards of fabric.
x × \(\frac{3}{4}\) = 9
x = 9 × \(\frac{4}{3}\)
x = 3 × 4 = 12
x = 12
she can make 12 skirts from 9 yards of fabric.
Question 12.
Part B
Explain how you determined which operation was needed to write the equation
Type below:
_____________
Answer: Division operation is needed to write the equation to know how many x skirts she can make from 9 yards of fabric.
Question 13.
Karen is working on her math homework. She solves the equation \(\frac{b}{8}\) = 56 and says that the solution is b = 7. Do you agree or disagree with Karen? Use words and numbers to support your answer. If her answer is incorrect, find the correct answer.
Type below:
_____________
Answer:
Karen is working on her math homework.
She solves the equation \(\frac{b}{8}\) = 56 and says that the solution is b = 7.
I Disagree with Karen.
b/8 = 56; multiply both sides by 8 to solve for b, and you get b = 448
Chapter 8 Review/Test Page No. 487
Question 14.
There are 70 historical fiction books in the school library. Historical fiction books make up \(\frac{1}{10}\) of the library’s collection. The equation \(\frac{1}{10}\)b = 70 can be used to find out how many books the library has. Solve the equation to find the total number of books in the library’s collection. Use numbers and words to explain how to solve \(\frac{1}{10}\)b = 70.
Type below:
_____________
Answer:
Given
Number of historical books = 70
The equation used to find the totals number of books in the library collection.
\(\frac{1}{10}\)b = 70
b = 70 × 10
b = 700
Hence there are 700 books in the library collection.
Question 15.
Andy drove 33 miles on Monday morning. This was \(\frac{3}{7}\) of the total number of miles he drove on Monday. Solve the equation \(\frac{3}{7}\)m = 33 to find the total number of miles Andy drove on Monday.
______ miles
Answer: 77 miles
Explanation:
Andy drove 33 miles on Monday morning.
This was \(\frac{3}{7}\) of the total number of miles he drove on Monday.
\(\frac{3}{7}\)m = 33
3 × m = 33 × 7
3 × m = 231
m = 231/3
m = 77 miles
Therefore the total number of miles Andy drove on Monday is 77 miles.
Question 16.
The maximum number of players allowed on a lacrosse team is 23. The inequality t≤23 represents the total number of players t allowed on the team.
Two possible solutions for the inequality are _____ and _____.
Two possible solutions for the inequality are _____ and _____
Answer:
The maximum number of players allowed on a lacrosse team is 23.
t ≤ 23
Thus the two possible solutions for the inequality are 22 and 23.
Question 17.
Mr. Charles needs to have at least 10 students sign up for homework help in order to use the computer lab. The inequality h ≥ 10 represents the number of students h who must sign up. Select possible solutions of the inequality. Mark all that apply.
Options:
a. 7
b. 8
c. 9
d. 10
e. 11
f. 12
Answer: D, E
Explanation:
Mr. Charles needs to have at least 10 students sign up for homework help in order to use the computer lab.
h ≥ 10
The number near to 10 is 10 and 11
Thus the correct answers are options D and E.
Chapter 8 Review/Test Page No. 488
Question 18.
The maximum capacity of the school auditorium is 420 people. Write an inequality for the situation. Tell what type of numbers the variable in the inequality can represent.
Type below:
_____________
Answer:
The maximum capacity of the school auditorium is 420 people
Let x be the maximum people
The inequality is x is less than or equal to 420.
x ≤ 420
Question 19.
Match the inequality to the word sentence it represents
Type below:
_____________
Answer:
Question 20.
Cydney graphed the inequality d ≤ 14.

Part A
Dylan said that 14 is not a solution of the inequality. Do you agree or disagree with Dylan? Use numbers and words to support your answer
Type below:
_____________
Answer: Agree with Dylan. Because the dark circle shows that it is not the solution.
Question 20.
Part B
Suppose Cydney’s graph had an empty circle at 14. Write the inequality represented by this graph.
Type below:
_____________
Answer: y < 14

Conclusion:
I believe the information provided in the above article regarding the Go Math Grade 6 Answer Key Chapter 8 Solutions of Equations is satisfactory for all the students. Get all the answer keys of all the chapters on ccssanswers.com For any queries you can post your comments in the below comment section.
