On this page, you will learn about the properties of natural numbers. Natural numbers are an important part of the number system, it is a set of whole numbers from 1 to infinity. The result of four arithmetic operations on natural numbers referred to Properties of natural numbers.
These numbers are used in our daily activities. Natural numbers come under real numbers, which include only the positive integers i.e., 1, 2, 3, 4, 5,…, and so on, excluding zero, fractions, decimals, and negative numbers. Remember that set of natural numbers does not include negative numbers or zero.
Read Some More Article:
Natural Numbers – Definition
Natural numbers are defined as the numbers which are positive integers and include numbers from 1 to infinity. These natural numbers are countable numbers and are preferred for calculation purposes. A set of natural numbers is denoted by the ‘N’.
N= {1,2,3,4,5,6,7,………..}
Where 1 is the smallest natural number and the sum of natural numbers from 1 to 100 is n(n+1)/2.
Types of Natural Numbers
There are two important types of natural numbers, namely:
1. Even Natural Numbers.
2. Odd Natural Numbers.
Even Natural Numbers: A system of natural numbers, which are divisible by 2 or multiplies of 2 is called a set of even numbers. Even natural number is denoted by ‘E’. Even numbers are infinite.
Therefore, E = {2, 4, 6, 8, 10, 12, 14, …….}.
Odd Natural Numbers: A natural number that is not divisible by 2 or not multiplies of 2 is called a set of odd numbers. An odd natural number is denoted by ‘O’. There are infinite odd natural numbers.
Therefore, O = { 1, 3, 5, 7, 9, 11, 13,…}.
Properties of Natural Numbers
Natural numbers have four important properties, which are as follows,
1. Closure Property
2. Distributive Property
3. Associative Property
4. Commutative Property
1. Closure Property:
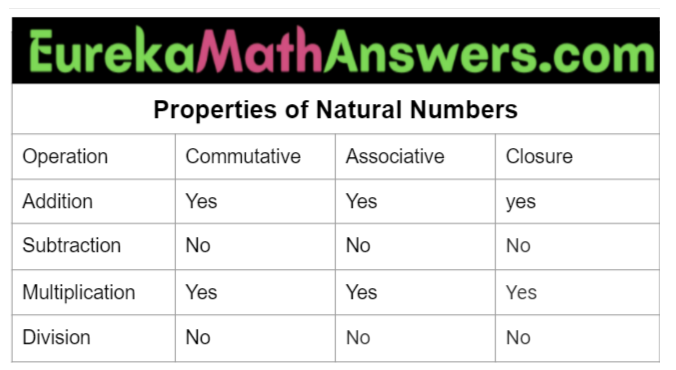
A natural number will be closed under addition and multiplication. It means adding or multiplying two natural numbers result will be in a natural number. While, for subtraction and division, natural numbers don’t follow the closure property.
Addition: When x and y are two natural numbers, x+y is also a natural number. Suppose an example, 3+3= 6, 7+4 = 11, and similarly, all the resultants are natural numbers.
Subtraction: When x and y are two natural numbers, but x-y might not result in natural numbers. Consider an example, 4-6 = -2, and 6-4 = 2.
Multiplication: For x and y are two natural numbers, so x*y is also a natural number. For example, 6*3 = 18, similarly all results from multiplication are natural numbers.
Division: For the two national numbers x and y, the division might or might not result in a natural number. For example, 12/3 = 4, and 12/5 =1.222
2. Commutative Property:
These property natural numbers state that the sum or product of two natural numbers remains the same even if you interchange the order of the numbers. Let us check for all four arithmetic operations,
Addition: When two natural numbers x and y, x + y = y + z is aslo a natural number.
Multiplication: For x, and y are two natural numbers, then x × y = y × x is also a natural number.
Subtraction: When x and y are two natural numbers, but x – y≠ y– x. So x-y and y-z is not natural number.
Division: For two natural numbers x and y, but x ÷ y ≠ x ÷ y (not equal). So these result values are not natural numbers.
Therefore, we can say that the set of natural numbers is commutative property under addition and multiplication but the case is not the same for subtraction and division. So, the commutative property of N is stated as follows: For all x, y ∈ N, x + y = y +x and x × y = y × x.
3. Distributive Property:
Distributive property of natural numbers states that expression with three numbers x, y, and z will be given in the form of X (Y+Z) then it will be resolved as XY+ XZ or X(Y-Z) = XY-XZ, which means that the operand x is distributed among the other two operands, y, and z.
- Multiplication of natural numbers is always distributive over the addition, So it will be expressed as, x × (y + z) = xy + xz.
- Multiplication of natural numbers is also distributive over subtraction, then the expression is, x × ( y – z) = xy – xz.
4. Associative Property:
The associative property of natural numbers states that the sum or addition and product or multiplication of any three natural numbers remain the same though the grouping of numbers is changed. The three national numbers, say, x, y and z, is x + (y + z) = (x + y) + z and x * (y * z) = (x * y) * z. Whereas, natural numbers do not follow the associative property for multiplication and division.
Addition: For natural numbers x, y and z, addition is associative, i.e. x + (y+z )= (x + y) + z. Consider an example, (12 +1) +1 = 14 = 12 + (1 + 1)
Multiplication: When x and y, z are three natural numbers, multiplication is an associative property, it means x*(y*z) = (x*y)*z. For an example of associative property is, (1*4)*2 = 8 = 1*(4*2).
Subtraction: For three natural numbers, x, y, and z. The subtraction is not an associative property, which means x-(y-z) is not equal to (x-y)-z. Consider an example, (3-7)- 1 = -5 but 3-(7-1) = -3.
Division: For three natural numbers a, b, and c division is not associative property, because x/(y/z) is not equal to (x/y)/z. For example, 2/(3/6) = 4 but (2/3)/6 = 0.11 both values are not equal.
Therefore, we can say that the set of natural numbers is associative under addition and multiplication but the case is not the same for subtraction and division.
FAQ’s on Properties of Natural Numbers
1. What are Natural numbers?
A. Generally, Counting numbers are referred to as Natural numbers. They start with 1 and go on 2, 3, 4, 5, and more. These are ones in which we can do the counting and we will be denoted by ‘N’. The only set of natural numbers are denoted by N. Natural numbers are from 1 to infinity.
2. Is the number 0 a natural number?
A. As we know that 0 is neither positive nor negative, it is however considered a whole number despite not being positive. Hence, it comes under a natural number as well. It will be presented on the number line to identify numbers in a set but we can’t use it to count anything.
3. Write the difference between the natural numbers and whole numbers?
A. Natural numbers only include positive numbers which started from 1 to infinity, whereas whole numbers are the combination of zero, positive numbers(natural numbers), and they start from 0 and end at infinite value.
4. List a few examples of Natural Numbers?
A. The examples of natural numbers are 2, 5, 7, 9, 13, 15, 18, 98, 117,..etc.
5. State the properties of Natural Numbers?
A. Natural numbers have four properties, which are as follows:
-
Closure Property – The Natural number follows closure property for addition and multiplication but not for the division and subtraction operations.
-
Commutative Property – In this, all the natural numbers follow commutative property only for addition and multiplication operations.
-
Associative Property – The set of natural numbers is associative under addition and multiplication but not subtraction and division.
-
Distributive Property – All given natural numbers, multiplication is distributive under the addition and subtraction operations.
Addition and multiplication are the operations for which a set of natural numbers follows as most of the properties. However, division and subtraction do not follow those properties.