This article aids you to know the concept of the Midpoint Theorem on Trapezium. In geometry, triangles and other shapes play a prominent role to construct geometrical shapes. Likewise, the trapezium is one of the concepts of geometry in mathematics. Trapezoids are also known as one of the types of quadrilaterals.
By the end of this page, kids will get complete intelligence on Trapezium and prove the given statement of the midpoint theorem on trapezium. Also, we will have a glimpse of the types of trapezoids along with the statement, construction, proof of the Mid-point Theorem on Trapezoid.
Also Read:
Trapezium – Definition
A trapezium has also been named a trapezoid and it is a four-sided closed shape polygon. A trapezium is a quadrilateral having two parallel sides of unequal length and the other two sides are non-parallel. The trapezium is a 2D figure. The sides which are parallel are termed as bases of the trapezoid and the non-parallel are termed as legs of a trapezium. The distance between the parallel sides is defined as the altitudes.
Types of Trapezoids
The trapezium is defined as a quadrilateral that can have one and only pair of parallel sides. The following are the different types of trapezoids.
- Isosceles Trapezoid: If two non-parallel sides of the same length or the legs of a trapezoid are in equal length is known as an isosceles trapezoid.
- Right Trapezoid: A right trapezoid has at least a pair of right angles.
- Scalene Trapezoid: In a trapezoid, neither of the sides nor the angles are of equal measure, we call it a scalene trapezoid.
Trapezoid Midsegement Theorem Proof
ABCD is a trapezium in which CD ∥ AB. E is the midpoint of DA. EG is drawn parallel to DC which meets CB at G. Prove that EG ∥ AB ∥ CD and EG = ½( AB + CD).
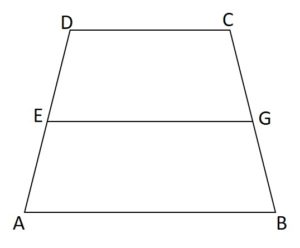
Given:
A trapezium ABCD, AB ∥ CD
where E and G are the midpoints of non-parallel sides DA, CB respectively.
To Prove:
Consider a trapezoid ABCD, prove that
EG ∥ AB ∥ CD and
EG = (AB + CD)/2.
Construction:
From the above trapezoid ABCD,
draw a line from point D to point B and join both the points.
Through midpoint E, construct another line where EH ∥ AB.
Since AB ∥ DC (given)
⇒ EH ∥ DC — (1)
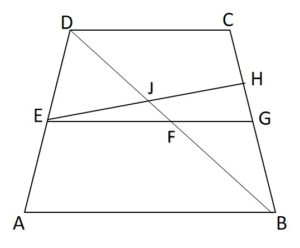
Proof:
In △DAB
E is the midpoint DA (given)
EJ ∥ AB by construction
⇒ J is the midpoint of DB. (by the converse of midpoint theorem)
Now, in △BCD
JH ∥ DC ( by equation 1)
J is the midpoint of DB.
⇒ H is the midpoint of CB (by the converse of midpoint theorem)
But, G is the midpoint of CB (from given)
⇒ H coincides with G ( as a line segment can have only one midpoint)
If H coincides with G
⇒ EH coincides with EG.
But, EH ∥ AB (by construction)
So, EH ∥ AB ∥ DC.
In ∆DAB, the line segment EF joins the midpoints of the sides DA and DB.
Therefore, EF = ½ AB. (by the midpoint theorem)
In ∆BCD, the line segment FG joins the midpoints of the sides DB and CB.
Therefore, FG = ½CD. ( by the midpoint theorem)
EF + FG = AB/2 + CD/2
⇒ EG = (AB+CD)/2
Hence, the statement is proved.
FAQ’s on Midpoint Theorem on Trapezium
1. What are Trapezoids?
Trapezoids are four-sided polygons that have two parallel sides and two non-parallel sides. Sometimes, a trapezoid is also known as a trapezium.
2. What is a trapezium when do you call a trapezium an isosceles trapezium?
A trapezium is a type of quadrilateral in which one pair of opposite sides are parallel. If the non-parallel sides of a trapezium are equal then a trapezium is called an isosceles trapezium.
3. Is trapezium a parallelogram?
No, a trapezium is a quadrilateral, not a parallelogram because a parallelogram has two pairs of parallel sides. But, a trapezium only has one pair of parallel sides.
4. Why is it called an isosceles trapezium?
The word “isosceles” means equal legs. In isosceles trapezoids have non-parallel sides are of the same measurement or length. These equal sides are called the “legs”.
5. How do you find the midpoint of a trapezium?