Practice with the help of Spectrum Math Grade 5 Answer Key Chapter 3 Lesson 3.9 Multiplication Practice regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapter 3 Lesson 3.9 Multiplication Practice Answers Key
Multiply.
Question 1.
a.
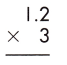
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
12 x 3 = 36
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 1
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 1, the resultant product must contain the decimal point after 1 digit from the rightmost place.
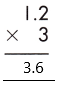
Therefore, 1.2 x 3 = 3.6
b.
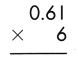
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
061 x 6 = 366
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 2
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digit from the rightmost place.
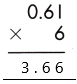
Therefore, 0.61 x 6 = 3.66
c.
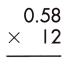
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
58 x 12 = 696
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 2
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
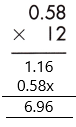
Therefore, 0.58 x 12 = 6.96
d.
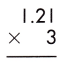
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
121 x 3 = 363
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 2
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
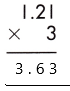
Therefore, 1.21 x 3 = 3.63
e.
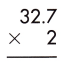
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
327 x 2 = 654
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 1
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 1, the resultant product must contain the decimal point after 1 digit from the rightmost place.
Therefore, 32.7 x 2 = 65.4
Question 2.
a.
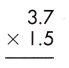
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
37 x 15 = 555
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 3.7 = 1
And the number of decimal places in 1.5 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 1 + 1 = 2
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
– Therefore, the product of the given decimals is 5.55
b.
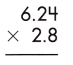
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
624 x 28 = 17472
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 6.24 = 2
And the number of decimal places in 2.8 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
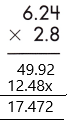
– Therefore, the product of the given decimals is 17.472
c.
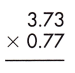
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
373 x 077 = 28721
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 3.73 = 2
And the number of decimal places in 0.77 = 2
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 2 = 4
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 4, the resultant product must contain the decimal point after 4 digits from the rightmost place.
– Therefore, the product of the given decimals is 2.8721
d.
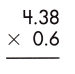
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
438 x 6 = 2628
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 4.38 = 2
And the number of decimal places in 0.6 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 2.628
e.
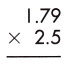
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
179 x 25 = 4475
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 1.79 = 2
And the number of decimal places in 2.5 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1= 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 4.475
Question 3.
a.
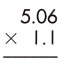
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
506 x 11 = 5566
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 5.06 = 2
And the number of decimal places in 1.1 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 5.566
b.
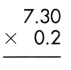
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
730 x 2 = 1460
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 7.30 = 2
And the number of decimal places in 0.2 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 1.460
c.

Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
346 x 87 = 30102
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 3.46 = 2
And the number of decimal places in 8.7 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 30.102
d.
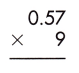
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
57 x 9 = 513
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 2
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
Therefore, 0.57 x 9 = 5.13
e.
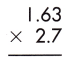
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
163 x 27 = 4401
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 1.63 = 2
And the number of decimal places in 2.7 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 4.401
Question 4.
a.
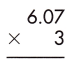
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
607 x 3 = 1821
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 2
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
Therefore, 6.07 x 3 = 18.21
b.
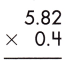
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
582 x 4 = 2328
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 5.82 = 2
And the number of decimal places in 0.4 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 2.328
c.
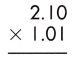
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
210 x 101 = 21210
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 2.10 = 2
And the number of decimal places in 1.01 = 2
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 2 = 4
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 4, the resultant product must contain the decimal point after 4 digits from the rightmost place.
– Therefore, the product of the given decimals is 2.1210
d.
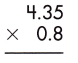
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
435 x 8 = 3480
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 4.35 = 2
And the number of decimal places in 0.8 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 3.480
e.
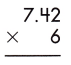
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
742 x 6 = 4452
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 2
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
Therefore, 7.42 x 6 = 44.52
Question 5.
a.
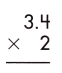
Answer:
Multiplying decimal numbers by whole numbers can be done as we do the multiplication of whole numbers. In this case, we should only take care of the decimal point. However, the operation of whole numbers multiplying with decimals
Steps:
1. Multiply both numbers as whole numbers, i.e. we ignore the decimal point here and proceed with the usual multiplication.
34 x 2 = 68
2. Count the number of digits to the right of the decimal point in the decimal number.
In this case, the required number of digits = 1
3. Put the decimal point in the product by counting the digits from the rightmost place.
As the total number of decimal places is 1, the resultant product must contain the decimal point after 1 digit from the rightmost place.
Therefore, 3.4 x 2 = 6.8
b.
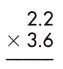
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
22 x 36 = 792
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 2.2 = 1
And the number of decimal places in 3.6 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 1 + 1 = 2
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
– Therefore, the product of the given decimals is 7.92
c.
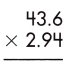
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
436 x 294 = 128184
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 43.6 = 1
And the number of decimal places in 2.94 = 2
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 1 + 2 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 128.184
d.
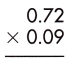
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
72 x 9 = 648
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 0.72 = 2
And the number of decimal places in 0.09 = 2
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 2 = 4
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 4, the resultant product must contain the decimal point after 4 digits from the rightmost place.
– Therefore, the product of the given decimals is 0.0648
e.

Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
991 x 12 = 11892
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 9.91 = 2
And the number of decimal places in 1.2 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 11.892