Practice with the help of Spectrum Math Grade 5 Answer Key Chapter 3 Pretest regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapter 3 Pretest Answers Key
Check What You Know
Question 1.
a.
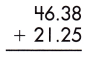
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
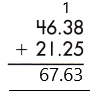
Therefore, the sum of the given decimals is 67.63
b.
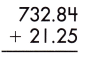
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
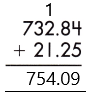
Therefore, the sum of the given decimals is 754.09
c.
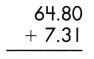
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
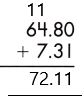
Therefore, the sum of the given decimals is 72.11
d.
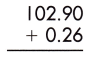
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
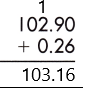
Therefore, the sum of the given decimals is 103.16
Question 2.
a.
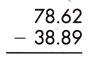
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
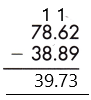
Therefore, the difference is 39.73
b.
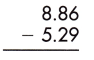
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
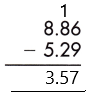
Therefore, the difference is 3.57
c.
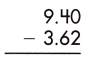
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
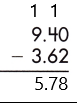
Therefore, the difference is 5.78
d.
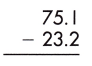
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
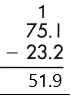
Therefore, the difference is 51.9
Question 3.
a.
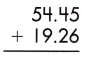
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
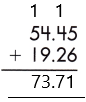
Therefore, the sum of the given decimals is 73.71
b.
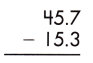
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
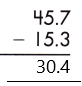
Therefore, the difference is 30.4
c.
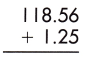
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
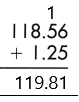
Therefore, the sum of the given decimals is 119.81
d.
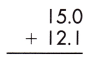
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
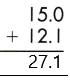
Therefore, the sum of the given decimals is 27.1
Multiply or divide.
Question 4.
a.
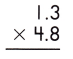
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
13 x 48 = 624

2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 1.3 = 1
And the number of decimal places in 4.8 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 1 + 1 = 2
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
– Therefore, the product of the given decimals is 6.24
b.
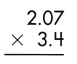
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
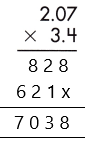
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 2.07 = 2
And the number of decimal places in 3.4 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 7.038
c.
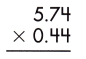
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
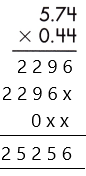
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 5.74 = 2
And the number of decimal places in 0.44 = 2
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 2 = 4
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 4, the resultant product must contain the decimal point after 4 digits from the rightmost place.
– Therefore, the product of the given decimals is 2.5256
d.
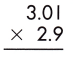
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
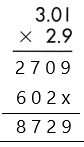
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 3.01 = 2
And the number of decimal places in 2.9 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 1= 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 8.729
Question 5.
a.
![]()
Answer:
When we divide decimals, we have to convert the divisor to a whole number by moving the decimal point to the right. Then, we carry the dividend’s decimal point up to the same number of places to the right and divide the resultant numbers in the usual way as we perform in regular long division.
Change the divisor 3.8 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
159.6 ÷ 38 = 4.20
and therefore:
15.96 ÷ 3.8 = 4.20
Both were calculated to 2 decimal places.
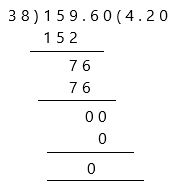
Therefore, the remainder is 0 and the quotient is 4.20
b.
![]()
Answer:
When we divide decimals, we have to convert the divisor to a whole number by moving the decimal point to the right. Then, we carry the dividend’s decimal point up to the same number of places to the right and divide the resultant numbers in the usual way as we perform in regular long division.
Change the divisor 0.12 to a whole number by moving the decimal point 2 places to the right. Then move the decimal point in the dividend the same, 2 places to the right.
We then have the equations:
48 ÷ 12 = 4.00
and therefore:
0.48 ÷ 0.12 = 4.00
Both were calculated to 2 decimal places.
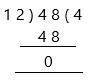
Therefore, the remainder is 0 and the quotient is 4
c.
![]()
Answer:
When we divide decimals, we have to convert the divisor to a whole number by moving the decimal point to the right. Then, we carry the dividend’s decimal point up to the same number of places to the right and divide the resultant numbers in the usual way as we perform in regular long division.
Change the divisor 1.75 to a whole number by moving the decimal point 2 places to the right. Then move the decimal point in the dividend the same, 2 places to the right.
We then have the equations:
6755 ÷ 175 = 38.60
and therefore:
67.55 ÷ 1.75 = 38.60
Both were calculated to 2 decimal places.
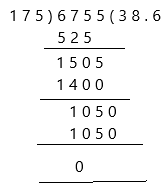
Therefore, the remainder is 0 and the quotient is 38.6
d.
![]()
Answer:
When we divide decimals, we have to convert the divisor to a whole number by moving the decimal point to the right. Then, we carry the dividend’s decimal point up to the same number of places to the right and divide the resultant numbers in the usual way as we perform in regular long division.
Change the divisor 0.25 to a whole number by moving the decimal point 2 places to the right. Then move the decimal point in the dividend the same, 2 places to the right.
We then have the equations:
30000 ÷ 25 = 1,200.00
and therefore:
300 ÷ 0.25 = 1,200.00
Both were calculated to 2 decimal places.
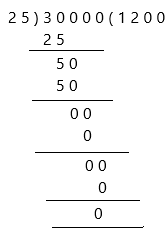
Therefore, the remainder is 0 and the quotient is 1200
Solve each problem.
Question 6.
In a recent week, the rainfall was 0.2 inches for Monday, 0.7 inches for Tuesday, and 1.6 inches for Wednesday. What was the total amount of rainfall for those 3 days?
The total amount of rainfall was ____ inches.
Answer:
The above-given:
The number of inches of rainfall for Monday = 0.2
The number of inches of rainfall for Tuesday = 0.7
The number of inches of rainfall for Wednesday = 1.6
The total rainfall for those 3 days = r
Based on the given conditions, we can formulate:
r = 0.2 + 0.7 + 1.6
r = 2.5
Therefore, the total amount of rainfall was 2.5 inches
Question 7.
Miranda wants to buy a tennis racket that costs $109.95. She has $68.50 saved from babysitting. How much more money does she need?
Miranda needs _____.
Answer:
The above-given:
The cost of tennis racket = $109.95
The amount she saved from babysitting = $68.50
The amount she need = x
x = 109.95 – 68.50
x = 41.45
Therefore, Miranda needs $41.45 more.
Question 8.
Julia went to the store and bought 3 items that cost $5.87, $21.62, and $11.48. What was the total cost of these items?
The total cost of the items was _____
Answer:
The above-given:
The number of items = 3
The given costs are $5.87, $21.62, and $11.48
The total cost of the items = x
x = 5.87 + 21.62 + 11.48
x = 38.97
Therefore, the total cost of the item was 38.97
Question 9.
If a car averages 23.2 miles per gallon of gasoline, how far can ¡t go on 15.25 gallons?
The car can go ______________ miles.
Answer:
The above-given:
The number of miles of average of car per gallon = 23.2
for 1 gallon – 23.2 miles
for 15.25 gallons – c miles
c = 23.2 x 15.25
c = 353.8
Therefore, the car can go 353.8 miles.
Question 10.
Maria bought gifts for 7 of her friends. She spent $86.66. If she spent the same amount on each of her friends, how much did she spend on each?
Maria spent ________________ on each friend.
Answer:
The above-given:
The number of friends = 7
The amount she spent on gifts = $86.66
The amount she spent on each gift = x
x = 86.66/7
x = 12.38
Therefore, Maria spent $12.38 on each friend.
Question 11.
A small tree was measured at 3.67 feet tall. It can grow to 25 times that height. What is the tallest height the tree can be expected to reach?
The tree can reach ____ feet.
Answer:
The above-given:
The height of the tree = 3.67
The number of times a tree can grow = 25
The tallest height of the tree = h
h = 3.67 x 25
h = 91.75
Therefore, the tree can reach 91.75 feet.