Go through the Spectrum Math Grade 6 Answer Key Chapter 6 Lesson 6.1 Calculating Area: Triangle and get the proper assistance needed during your homework.
Spectrum Math Grade 6 Chapter 6 Lesson 6.1 Calculating Area: Triangle Answers Key
The area (A) of a triangle is one-half the of the base (b) times the height (h).
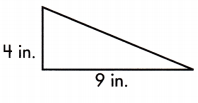
A = \(\frac{1}{2}\) × 9 × 4
= \(\frac{1}{2}\) × 36
= 18
A = 18 square inches
A = \(\frac{1}{2}\) × b × h
or
A = \(\frac{1}{2}\)bh
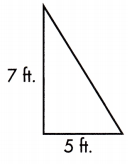
A = \(\frac{1}{2}\) × 5 × 7
= \(\frac{1}{2}\) × 35
= 17\(\frac{1}{2}\)
A = 17\(\frac{1}{2}\) square inches
Find the area of each right triangle.
Question 1.
a.
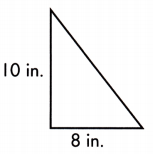
A = ____ sq. in.
Answer:
The base length of given triangle is 8 in. and the perpendicular line from the base to the opposite vertex is the height which is 10 in. long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 8 × 10
= \(\frac{1}{2}\) × 80
= 40 sq.in
Thus, the area of triangle will be 40 sq.in
b.
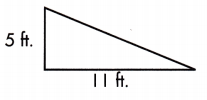
A = ____ sq. ft.
Answer:
The base length of given triangle is 11 ft and the perpendicular line from the base to the opposite vertex is the height which is 5 ft long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 11 × 5
= \(\frac{1}{2}\) × 55
= 27.5 sq.ft
Thus, the area of triangle will be 27.5 sq.ft
Question 2.
a.
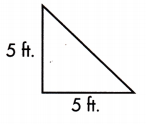
A = ____ sq. ft.
Answer:
The base length of given triangle is 5 ft and the perpendicular line from the base to the opposite vertex is the height which is 5 ft long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 5 × 5
= \(\frac{1}{2}\) × 25
= 12.5 sq.ft
Thus, the area of triangle will be 12.5 sq.ft
b.
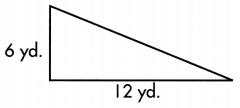
A = ____ sq. yd.
Answer:
The base length of given triangle is 12 yd and the perpendicular line from the base to the opposite vertex is the height which is 6 yd long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 12 × 6
= \(\frac{1}{2}\) × 72
= 36 sq.yd
Thus, the area of triangle will be 36 sq.yd
The area of a triangle is related to the area of a rectangle.
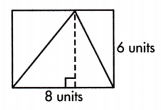
The dashed line indicates the height of the triangle, rectangle: A = 8 × 6 = 48 sq. units triangle: A = \(\frac{1}{2}\)(8) (6) = 24 sq. units
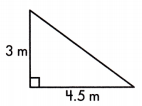
A = \(\frac{1}{2}\)(4.5)(3) = 6\(\frac{3}{4}\)sq. m
Notice that in a right triangle the height is the length of one of the legs. This is not the case with acute and obtuse triangles.
Find the area of each triangle below.
Question 1.
a.
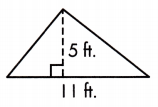
A = ____ sq. ft.
Answer:
The base length of given triangle is 11 ft and the dashed line is the height which is 5 ft long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 11 × 5
= \(\frac{1}{2}\) × 55
= 27.5 sq.ft
Thus, the area of triangle will be 27.5 sq.ft
b.
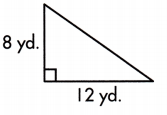
A = ____ sq. yd.
Answer:
The base length of given triangle is 12 yd and the perpendicular line from the base to the opposite vertex is the height which is 8 yd long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 12 × 8
= \(\frac{1}{2}\) × 96
= 48 sq.yd
Thus, the area of triangle will be 48 sq.yd
c.
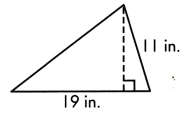
A = ____ sq. in.
Answer:
The base length of given triangle is 19 in. and the dashed line is the height which is 11 in. long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 19 × 11
= \(\frac{1}{2}\) × 209
= 104.5 sq.in.
Thus, the area of triangle will be 104.5 sq.in.
Question 2.
a.
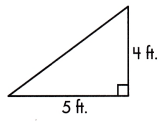
A = ____ sq. ft.
Answer:
The base length of given triangle is 5 ft and the perpendicular line from the base to the opposite vertex is the height which is 4 ft long
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 5 × 4
= \(\frac{1}{2}\) × 20
= 10 sq.ft
Thus, the area of triangle will be 10 sq.ft
b.
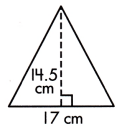
A = ____ sq. cm.
Answer:
The base length of given triangle is 17 cm and the dashed line is the height which is 14.5 cm long.
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 17 × 14.5
= \(\frac{1}{2}\) × 246.5
= 123.25 sq.cm
Thus, the area of triangle will be 123.25 sq.cm
c.
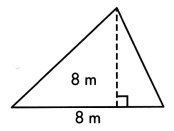
A = ____ sq. m.
Answer:
The base length of given triangle is 8 m and the dashed line is the height which is 8 m long.
A = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 8 × 8
= \(\frac{1}{2}\) × 64
= 32 sq.m
Thus, the area of triangle will be 32 sq.m
Try More: