Go through the Spectrum Math Grade 6 Answer Key Chapter 6 Lesson 6.3 Calculating Area: Other Polygons and get the proper assistance needed during your homework.
Spectrum Math Grade 6 Chapter 6 Lesson 6.3 Calculating Area: Other Polygons Answers Key
Calculating Area: Other Polygons
To find the area of an irregular shape, separate the shape into its component figures and find the area of each one.
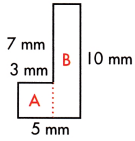
This figure can be divided into two rectangles, as shown by the dotted line.
To find the missing side measurement of shape A, look at the vertical measurements you already know: 10 mm and 7 mm. Because the missing side must be the difference between 10 and 7, subtract to get the answer: 10 — 7 = 3 mm.
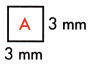
To find the area of shape A, multiply l × w.
3 × 3 = 9 mm
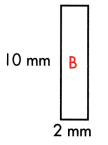
Follow the same steps to find the area of shape B.
5 – 3 = 2 mm
A = 10 × 2 = 20 mm
Then, add the two areas together to get the area of the entire irregular shape.
9 + 20 = 29 square mm
Find the area of each figure.
Question 1.
a.
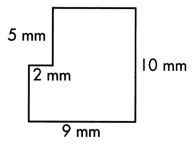
A = ____ sq. mm
Answer:
This figure can be divided into two rectangles, as shown by the dotted line.
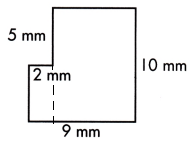
The small rectangle measures 2 mm wide and length will be 10-5=5 mm.
Area of smaller rectangle = length×width
= 5×2
= 10 sq.mm
The larger rectangle measures 10 mm long and 9-2 = 7 mm
Area of larger rectangle = length×width
= 10×7
= 70 sq.mm
Area of complete polygon = Area of smaller rectangle + Area of larger rectangle
= 10+70
= 80 sq.mm
b.
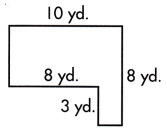
A = ____ sq. yd.
Answer:
This figure can be divided into two rectangles, as shown by the dotted line.
The small rectangle measures 3 yd long and width will be 10-8 = 2 yd.
Area of smaller rectangle = length×width
= 3×2
= 6 sq.yd
The larger rectangle measures 10 yd long and 8-3 = 5 yd
Area of larger rectangle = length×width
= 10×5
= 50 sq.yd
Area of complete polygon = Area of smaller rectangle + Area of larger rectangle
= 6+50
= 56 sq.yd
c.
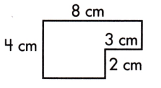
A = ____ sq. cm.
Answer:
This figure can be divided into two rectangles, as shown by the dotted line.
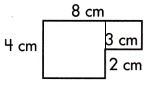
The small rectangle measures 4-2=2 cm long and width will be 3 cm.
Area of smaller rectangle = length×width
= 3×2
= 6 sq.cm
The larger rectangle measures 4 cm long and 8-3 = 5 yd
Area of larger rectangle = length×width
= 4×5
= 20 sq.cm
Area of complete polygon = Area of smaller rectangle + Area of larger rectangle
= 6+20
= 26 sq.cm
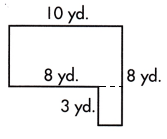
Question 2.
a.
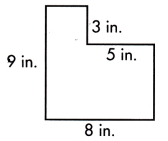
A = ____ sq. in.
Answer:
This figure can be divided into two rectangles, as shown by the dotted line.
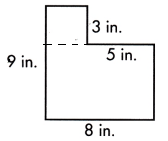
The small rectangle measures 8-5=3 in wide and length will be 3 in.
Area of smaller rectangle or square = length×width
= 3×3
= 9 sq.in
The larger rectangle measures 9-3 = 6 in. long and 8 in. wide
Area of larger rectangle = length×width
= 6×8
= 48 sq.in
Area of complete polygon = Area of smaller rectangle + Area of larger rectangle
= 9+48
= 57 sq.in
b.
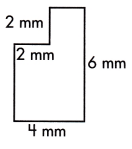
A = ____ sq. mm
Answer:
This figure can be divided into two rectangles, as shown by the dotted line.
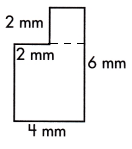
The small rectangle measures 4-2=2 mm wide and length will be 2 mm.
Area of smaller rectangle or square = length×width
= 2×2
= 4 sq.mm
The larger rectangle measures 6-2 = 4 mm long and 4 mm wide
Area of larger rectangle or square = length×width
= 4×4
= 16 sq.mm
Area of complete polygon = Area of smaller rectangle + Area of larger rectangle
= 4+16
= 20 sq.mm
c.
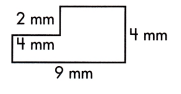
A = ____ sq. mm
Answer:
This figure can be divided into two rectangles, as shown by the dotted line.
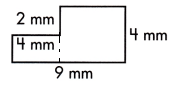
The small rectangle measures 4-2=2 mm long and width will be 4 mm.
Area of smaller rectangle or square = length×width
= 2×4
= 8 sq.mm
The larger rectangle measures 9-4 = 5 mm long and 4 mm wide
Area of larger rectangle or square = length×width
= 5×4
= 20 sq.mm
Area of complete polygon = Area of smaller rectangle + Area of larger rectangle
= 8+20
= 28 sq.mm
Some irregular shapes are made up of more than one type of figure.
This figure can be divided into a square and a triangle.
area of square
A = 6 × 6 = 36
area of triangle
A = \(\frac{1}{2}\) × 3 × 6 = 9
The area of the figure is 36 + 9 = 45 square meters.
Find the area of each figure.
Question 1.
a.
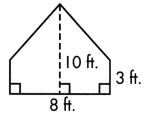
A = ____ sq. ft.
Answer:
This figure can be divided into one rectangle and one triangle, as shown by the dotted line.
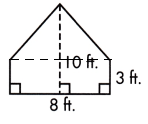
The base of the triangle is 8ft and the height will be 10-3=7 ft.
Area of trinagle will be = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 8 × 7
= 4 × 7
= 28 sq.ft
The base of the rectangle 8ft and height is 3ft.
Area of rectangle = length × width
= 8×3
= 24 sq.ft
Area of polygon = Area of triangle + Area of rectangle
= 28+24
= 52 sq.ft
b.
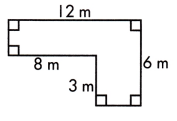
A = ____ sq. m.
Answer:
This figure can be divided into two rectangles, as shown by the dotted line.
The small rectangle measures 6-3=3 m long and width will be 8 m.
Area of smaller rectangle or square = length×width
= 3×8
= 24 sq.m
The larger rectangle measures 12-8 = 4 m wide and 6 m long
Area of larger rectangle or square = length×width
= 4×6
= 24 sq.m
Area of complete polygon = Area of smaller rectangle + Area of larger rectangle
= 24+24
= 48 sq.m
c.
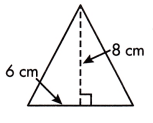
A = ____ sq. cm.
Answer:
Given triangle has base length of 6 cm and height of 8 cm
Area of triangle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 6 × 8
= 48÷2
= 24 sq.cm
Thus, the area of triangle is 24 sq.cm
Question 2.
a.
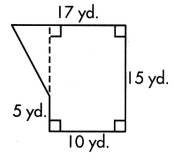
A = ____ sq. yd.
Answer:
Height of triangle = 17-10 = 7 yd
Base of triangle = 15-5 = 10 yd
Area of triangle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 10 × 7
= 70÷2
= 35 sq.yd
The length of rectangle is 15 yd and 10 yd wide.
Area of rectangle = length×width
= 15×10
= 150 sq.yd
Area of polygon = Area of triangle + Area of rectangle
= 35 + 150
= 185 sq.yd
b.
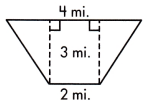
A = ____ sq. mi.
Answer:
The given trapezium has two lengths of 4 mi and 2 mi.
Sum of the sides will be 4+2 = 6 mi.
The height of the trapezium is 3 mi.
Area of trapezium = \(\frac{1}{2}\) × (a+b) × h
= \(\frac{1}{2}\) × (a+b) × h
= \(\frac{1}{2}\) × 6 × 3
= 18÷2
= 9 sq.mi
Thus, the area of trapezium will be 9 sq.mi
c.
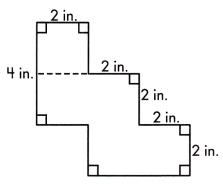
A = ____ sq. in.
Answer:
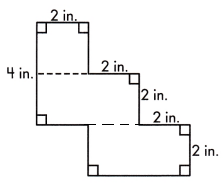
The square measures 2 in.
Area of square will be length×length
= 2×2
= 4 sq.in
The rectangle has length of 4 in and is 2 in. wide
Area of rectangle = length×width
= 4×2
= 8 sq.in
Area of polygon will be Area of square+Area of rectangle+Area of rectangle
= 4+8+8
= 20 sq.in
Thus, the area of polygon will be 20 sq.in
Read More: