In Mathematics, Area and Perimeter are two important properties of two-dimensional shapes which is used in our day-to-day life. The Area and Perimeter of different combined figures are explained here. Before that, you must learn about different basic shapes such as triangle, square, rectangle, circle, and sphere, etc. The Perimeter is defined as the distance of the boundary of the shape whereas the Area will explain the region occupied by it.
In this article, we will discuss the definition of Combined Figures, how to find Area and Perimeter of Combined Figures, Solved Example problems, and so on. There are various types of shapes but commonly used are square, rectangle, triangle, circle.
Also, Read :
- Areas of Irregular Figures
- Worksheet on Area and Perimeter of Triangle
- Worksheet on Area and Perimeter of Squares
Combined Figures – Definition
Combined Figures is defined as shapes that are composed of a combination of simpler shapes. Each shape has its own area and perimeter formula. It is applicable to any shape and size whether it is regular or irregular.
To find the perimeter, add all the outside sides of our shape, and find the area we divide our shapes into simple shapes, calculate the area of those shapes separately, and then add areas up to get total.
How to find Area and Perimeter of Combined Figures?
The following are the steps for finding the area and perimeter of combined figures:
How to find Area of Combined Shapes?
Step 1: First, divide the compound shape into a basic regular shape.
Step 2: Next, find each basic shape area separately.
Step 3: Then Add all the areas of basic shapes together.
Step 4: Now, write the final answer in square units.
How to find the Perimeter of Combined Figures?
The perimeter of the combined figure is the length of the outline of a shape. To find the perimeter of any shape like rectangle, square, and so on you have to add all the lengths of four sides. Consider x is in this case the length of the rectangle and y is the width of the rectangle.
Read Similar Shapes:
Area and Perimeter of Combined Shapes Examples
Problem 1: Find the area and perimeter of the following combined figures. The below- combined figure consists of a square and a triangle.
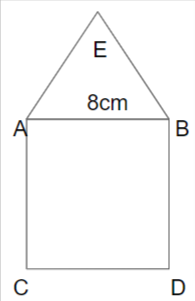
Solution:
As given in the question, the combined figure is given.
Now, we will find the area and perimeter of a combined figure.
The combined figure consists of a square and equilateral triangle.
First, find the area of a square and the area of an equilateral triangle.
We know, the formulas of the area of a square and the area of an equilateral triangle.
The area of a square is a² and the area of an equilateral triangle is (√3/4) × a2 square units.
Substitute the value in the above formulas, we get
Area of combined figures = Area of a square + Area of an equilateral triangle.
A= a² + (√3/4) × a2
A = 8 x 8 x (1.732/4) x 8 x 8 (√3 = 1.732)
A = 64 x 1.732 x 16 = 1774 sq.units.
So, the area of combined figures is 1774 sq. units.
Now, find the perimeter. So, the perimeter of combined figures is AB+BC+CD+DE+EA
P= 8+8+8+8+8 = 40 cm.
Hence the area and perimeter of the combined figure are 1774 sq. units and 40 cm.
Problem 2: A combined Figure is as given below. Find the area and perimeter of that Figure?
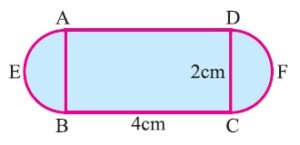
Solution:
The given figure is a combination of a rectangle and two circles. ABCD is a rectangle and AEB, DFC is two semicircles both are having equal area.
The length of the rectangle is l = 4cm.
The breadth of the rectangle is, b = 2cm.
The diameter of a semicircle is 2 cm.
The radius of a semicircle is r = 22cm.
Now, we will find the area and perimeter of the combined figure.
So, the perimeter of the given combined figure is, AD+BC+AEB+DFC
P= 4+4+2×21 (circumference of a circle)
P= 8+ 2 x 21 x 2πr = 8+2 x 722 x 1
P= 8+2 x 3.14 = 14.28 cm.
So, the perimeter of the given combined figure is 14.28 cm.
Next, find the area of combined figures.
Area of a combined figure = Area of a rectangle (ABCD)+ 2 x Area of a semicircle.
After substituting the values, we will get the value that is
A = l x b + 2 x 2πr2
A= 4×2+2x7x22x1x1 = 11.14 cm2
Therefore, the area and perimeter of the given combined figure are 11.14 cm2 and 14.28 cm.
Problem 3: Find the area of a below-given combined figure.
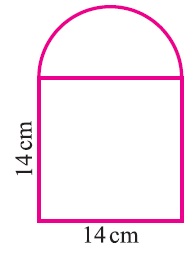
Solution:
As given in the question, the figures consist of a square and semicircle.
Now, we will find the area of a combined figure.
So, the Area of a combined figure = Area of a square + Area of a semicircle
A = sxs+1/2 π(rxr) = 14 X 14 + (1/2)(22/7)(7 x 7) = 77+196
A= 273 cm2
Thus the area of a given combined figure is 273 cm2.
Problem 4: Find the perimeter of a given figure.
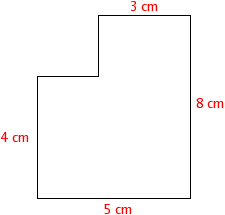
Solution:
In the given question consists of a figure.
Now, we will find the perimeter of that figure.
Perimeter means adding all the lengths of shapes.
Perimeter of a combined figure is,
P = 4 cm+3 cm+8 cm+5cm.
P = 20cm
Hence, the Perimeter of a given combined figure is 20cm.
Problem 5: The figure is shown in the below figure. Using figure values find the area and perimeter of a combined figure?
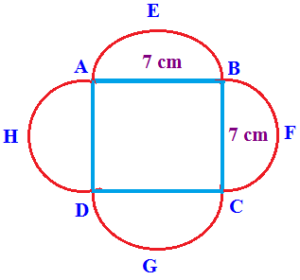
Solution:
The given figure consists of four semi-circles and one square.
Now, we will find the perimeter and area of the figure.
The diameter of each semicircle is 7cm.
The length of each square side is 7cm.
Using the diameter value, we will find the radius.
Radius = d/2 = 7/2 = 3.5cm.
First, find the perimeter, we have to add the four semicircles and a square. The resultant sum is Perimeter.
So, the perimeter of a given figure = 4 x Perimeter of semicircles + perimeter of a square.
P = 4 (Πr )+ 4a = (22/7)(3.5 cm) + 4(7).
P = 4(22 x 0.5 )+ 28 = 44 cm + 28 cm = 72 cm.
Thus the perimeter of the given figure is 72cm.
Next, find the area of a given figure.
Area of a combined figure = Area of 4 semicircles + Area of a square.
The Area of 1 semicircle is Πr²/2
= (1/2) x (22/7) x (7/2)²= (1/2) x (22/7) x (7/2) x (7/2)
= (1/2) x 11 x (7/2)= 77/4= 19.25 cm²
Then, the Area of 4 semi circles = 4 (19.25)= 77cm².
The area of a square is a²= (7)²= 7 x 7 = 49 cm².
Area of a combined figure = 19.25 cm² + 49 cm² = 126 cm².
Hence, the area and perimeter of a given combined figure are 72 cm and 126 cm².