Big Ideas Math Algebra 1 Answers Chapter 2 Solving Linear Inequalities is available on this page. So, the students who are searching for the BIM Algebra 1 Chapter 2 Solving Linear Inequalities Solution Key can Download free pdf from here. Your Practice session without Algebra 1 Big Ideas Maths Ch 2 Solving Linear Inequalities Answer Key incomplete. It helps not only in improving your subject knowledge but also helps you to score better marks in the exams. Thus Refer to Big Ideas Math Algebra 1 Answers Chapter 2 Solving Linear Inequalities and learn different methods to solve the problems.
Big Ideas Math Book Algebra 1 Answer Key Chapter 2 Solving Linear Inequalities
Students of high school can learn how to solve linear inequalities in a quick and fun way from here. Linear inequalities are the expressions where any two values are compared by the inequality symbols such as, ‘<‘, ‘>’, ‘≤’ or ‘≥’. You can find step-by-step solutions for lessons, exercises, Quiz, Chapter Tests, Chapter Review, and Cumulative Assessments with a brief explanation. So, students who are unable to solve the problems in linear inequalities can make use of the below-provided links and finish their assignments in time.
- Solving Linear Inequalities Maintaining Mathematical Proficiency – Page 51
- Solving Linear Inequalities Mathematical Practices – Page 52
- Lesson 2.1 Writing and Graphing Inequalities – Page(53-60)
- Writing and Graphing Inequalities 2.1 Exercises – Page(58-60)
- Lesson 2.2 Solving Inequalities Using Addition or Subtraction – Page(61-66)
- Solving Inequalities Using Addition or Subtraction 2.2 Exercises – Page(65-66)
- Lesson 2.3 Solving Inequalities Using Multiplication or Division – Page(67-72)
- Solving Inequalities Using Multiplication or Division 2.3 Exercises – Page(71-72)
- Lesson 2.4 Solving Multi-step Inequalities – Page(73-78)
- Solving Multi-step Inequalities 2.4 Exercises – Page(77-78)
- Solving Linear Inequalities Study Skills: Analyzing Your Errors – Page 79
- Solving Linear Inequalities Maintaining 2.1 – 2.4 Quiz – Page 80
- Lesson 2.5 Solving Compound Inequalities – Page(81-86)
- Solving Compound Inequalities 2.5 Exercises – Page(85-86)
- Lesson 2.6 Solving Absolute Value Inequalities – Page(87-92)
- Solving Absolute Value Inequalities 2.6 Exercises – Page(91-92)
- Solving Linear Inequalities Performance Task: Grading Calculations – Page 93
- Solving Linear Inequalities Chapter Review – Page(94-96)
- Solving Linear Inequalities Chapter Test – Page 97
- Solving Linear Inequalities Maintaining Cumulative Assessment – Page(98-99)
Solving Linear Inequalities Maintaining Mathematical Proficiency
Graph the number.
Question 1.
6
Answer:
The number line representing 6 is:
The number line represents the numbers from a negative value to a positive value. Mark 6 on the number line.
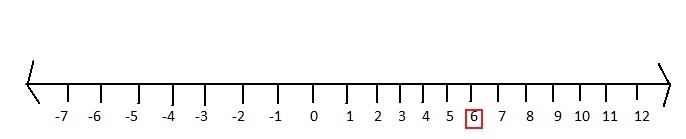
Question 2.
| 2 |
Answer:
The number line represents the numbers from a negative value to a positive value.
| x | = x for x > 0
| x | = -x for x < 0
|2| = 2 or -2
Mark 2 and -2 on the number line.
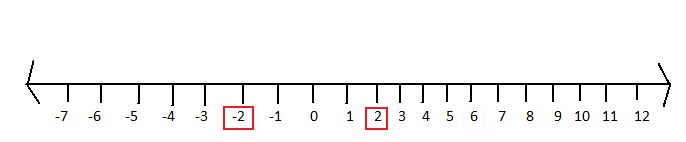
Question 3.
| -1 |
Answer:
Given,
| -1 |
The number line represents the numbers from a negative value to a positive value.
| -x | = x for x > 0
| -x | = -x for x < 0
Mark -1 and 1 on the number line.
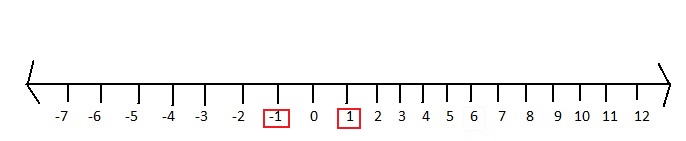
Question 4.
2 + | -2 |
Answer:
Given,
2 + | -2 |
The number line represents the numbers from a negative value to a positive value.
| -x | =x for x > 0
| -x | = -x for x < 0
2 + | -2 | = 2 + 2 2 + | – 2 | = 2 – 2
= 4 = 0
Mark 4 and 0 on the number line.
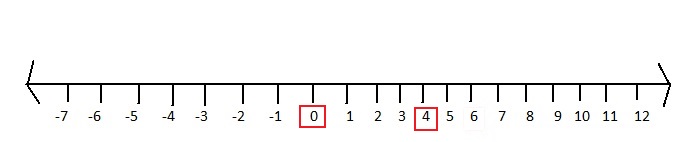
Question 5.
1 – | -4 |
Answer:
Given,
1 – | – 4 |
| -x | = x for x > 0
| – x | = -x for x < 0
1 – | – 4 | = 1 – 4 1 – | – 4 | = 1 – ( -4 )
= -3 = 5
The number line represents the numbers from a negative value to a positive value. Mark -3 and 5 on the below number line.
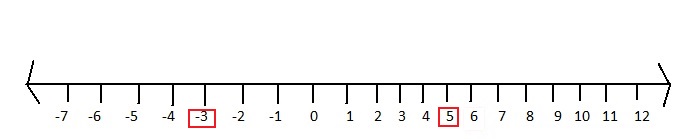
Question 6.
-5 + | 3 |
Answer:
Given,
-5 + | 3 |
| x | = x for x > 0
| x | = -x for x < 0
-5 + | 3 | = -5 + 3 -5 + | 3 | = -5 -3
= -2 = -8
The number line represents the numbers from a negative value to a positive value. Mark -2 and -8 on the number line.

Complete the statement with <, >, or =.
Question 7.
![]()
Answer:
Write the numbers in ascending order.
-9, -8, -7, -6, -5, -4,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
2 < 9
Question 8.
![]()
Answer:
Write the numbers in ascending order.
-9, -8, -7, -6, -5, -4,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
-6 < 5
Question 9.
![]()
Answer:
Write the numbers in ascending order.
-9, -8, -7, -6, -5, -4,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The greater number in the positive integers is the lesser number in the negative integers
-12 < -4
Question 10.
![]()
Answer:
Write the numbers in ascending order.
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The greater number in the positive integers is the lesser number in the negative integers
-7 > -13
Question 11.
![]()
Answer:
Given,
![]()
| -x | = x for x > 0
| -x | = -x for x < 0
Write the numbers in ascending order.
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The greater number in the positive integers is the lesser number in the negative integers
8 = 8 ( or ) -8 = -8
Question 12.
![]()
Answer:
![]()
| -x | = x for x > 0
| -x | = -x for x < 0
Write the numbers in ascending order.
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The greater number in the positive integers is the lesser number in the negative integers
-10 < 18 ( or ) -10 > -18
Question 13.
ABSTRACT REASONING
A number a is to the left of a number b on the number line. How do the numbers -a and -b compare?
Answer:
It is given that a number a is to the left of a number b on the number line.
Mark -a and -b on the number line.

-a > -b
Solving Linear Inequalities Mathematical Practices
Monitoring Progress
Use a graphing calculator to solve the inequality.
Question 1.
2x + 3 < x – 1
Answer:
Given,
2x + 3 < x – 1
2x – x < -1 – 3
x < – 4
The representation of the solved inequality in the number line is

Question 2.
-x – 1 > -2x + 2
Answer:
Given,
-x – 1 > -2x + 2
-x + 2x > 2 + 1
x > 3
The representation of the solved inequality in the number line is

Question 3.
\(\frac{1}{2}\)x + 1 > \(\frac{3}{2}\)x + 3
Answer:
Given,
\(\frac{1}{2}\)x + 1 > \(\frac{3}{2}\)x + 3
\(\frac{1}{2}\)x – \(\frac{3}{2}\)x > 3 – 1
\(\frac{1 – 3}{2}\)x > 2
\(\frac{-2}{2}\)x > 2
\(\frac{-1}{1}\)x > 2
-x > 2
x > -2
The representation of the solved inequality in the number line is

Lesson 2.1 Writing and Graphing Inequalities
Essential Question
How can you use an inequality to describe a real-life statement?
Answer:
Inequalities are arguably used more often in “real life” than equalities. Inequality is just a relationship between two amounts, in which the amounts are not the same.
Example:
She completed her work before anyone else. i.e., her finish time was less than everyone else
EXPLORATION 1
Writing and Graphing Inequalities
Work with a partner. Write an inequality for each statement. Then sketch the graph of the numbers that make each inequality true.
a. Statement The temperature t in Sweden is at least -10°C.
Inequality ![]()
Graph 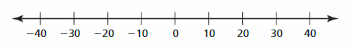
Answer:
The temperature t in Sweden is at least -10°C
The meaning of the above statement is that the temperature of Sweden is -10°C or greater than -10°C
The representation of the temperature of Sweden in the graph is:

b. Statement The elevation e of Alabama is at most 2407 feet.
Inequality ![]()
Graph 
Answer:
The elevation ‘ e ‘ of Alabama is at most 2,407 feet
The gap between each elevation is 1,000 feet
The elevation of Alabama will come between 2000 and 3000 in the number line


EXPLORATION 2
Writing Inequalities
Work with a partner. Write an inequality for each graph. Then, in other words, describe all the values of x that make each inequality true.
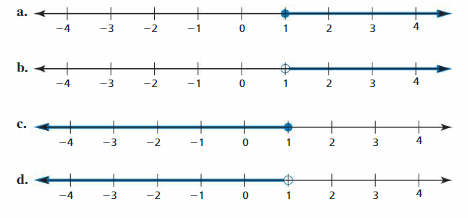
Answer:
a) The value of x is marked from 1 to 4
The inequality representing the given number line is:
x ≥ 1
b) The value of x marked after 1 till the end of the number line
The inequality representing the given number line is:
x > 1
c) The value of x is marked from 1 till the end of the left side of the number line.
The inequality representing the given number line is:
x ≤ 1
d) The value of x marked before 1 till the end of the left side of the number line
The inequality representing the given number lie is:
x < 1
Communicate Your Answer
Question 3.
How can you use an inequality to describe a real-life statement?
Answer:
Inequalities are arguably used more often in “real life” than equalities. Inequality is just a relationship between two amounts, in which the amounts are not the same.
Example:
A ball in the net is worth two in the bush. i.e., the value of a single ball in the net is greater than the value of a single ball in the bush.
Question 4.
Write a real-life statement that involves each inequality.
a. x < 3.5
b. x ≤ 6
c. x > -2
d. x ≥ 10
Answer:
a) x < 3.5
The number of birds that are less than the height of 3.5 inches
b) x ≤ 6
The number of people that are buying mobiles from a mobile store
c) x > -2
The number of integers that are greater than -2
d) x ≥ 10
The number of chocolates that are distributed greater than or equal to 10 children
2.1 Lesson
Monitoring Progress
Write the sentence as an inequality.
Question 1.
A number b is fewer than 30.4.
Answer:
Given,
A number b is fewer than 30.4
b < 30.4
Question 2.
–\(\frac{7}{10}\) is at least twice a number k minus 4.
Answer:
Given,
–\(\frac{7}{10}\) is at least twice a number k minus 4.
The representation of the given sentence in the form of inequality is
–\(\frac{7}{10}\) = 2k – 4
Tell whether −6 is a solution to the inequality.
Question 3.
c + 4 < -1
Answer:
Given,
c + 4 < -1
c = -4 – 1
c = -5
-6 is not a solution to the given inequality
Question 4.
10 ≤ 3 – m
Answer:
Given,
10 ≤ 3 – m
-m ≤ 10 – 3
-m ≤ 7
m ≤ -7
-6 is not a solution to the given inequality
Question 5.
21 ÷ x ≥ -3.5
Answer:
Given,
21 ÷ x ≥ -3.5
-21 ÷ 3.5 ≥ x
-210 ÷ 35 ≥ x
-6 ≥ x
x ≤ -6
-6 is a solution to the given inequality
Question 6.
4x – 25 > -2
Answer:
Given,
4x – 25 > -2
4x > -2 + 25
4x > 23
x > 23 ÷ 4
x > 5.75
-6 is not a solution to the given inequality
Graph the inequality.
Question 7.
b > -8
Answer:
Given,
b > -8

Question 8.
1.4 ≥ g
Answer:
Given,
1.4 ≥ g
g ≤ 1.4

Question 9.
r < \(\frac{1}{2}\)
Answer:
Given,
r < \(\frac{1}{2}\)
r < 0.5

Question 10.
v ≥ \(\sqrt{36}\)
Answer:
Given,
v > \(\sqrt{36}\)
\(\sqrt{36}\) = 6
v > 6

Question 11.
Write an inequality that represents the graph.
![]()
Answer:
The marked line is from -6 and continued after -6 till the last number on the right side of the number line.
The representation of the given number line in the form of inequality is x ≥ -6
Writing and Graphing Inequalities 2.1 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A mathematical sentence using the symbols <, >, ≤, or ≥ is called a(n)_______.
Answer:
A mathematical sentence using the symbols <, >, ≤, or ≥ is called an inequality.
Question 2.
VOCABULARY
Is 5 in the solution set of x + 3 > 8? Explain.
Answer:
Given,
x + 3 > 8
x > 8 – 3
x > 5
5 is not the solution to the given inequality
Question 3.
ATTENDING TO PRECISION
Describe how to graph an inequality.
Answer:

Question 4.
DIFFERENT WORDS, SAME QUESTION
Which is different? Write “both” inequalities.

Answer:
The given inequalities in the worded form are:
a) The given worded form in the form of inequality is:
w ≥ -7
b) The given worded form in the form of inequality is:
w > -7
c) The given worded form in the form of inequality is:
w ≥ -7
d) The given worded form in the form of inequality is:
w ≥ -7
Monitoring Progress and Modeling with Mathematics
In Exercises 5–12, write the sentence as an inequality.
Question 5.
A number x is greater than 3.
Answer:
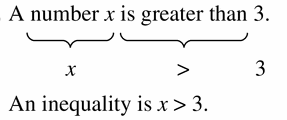
Question 6.
A number n plus 7 is less than or equal to 9.
Answer:
Given,
A number n plus 7 is less than or equal to 9
The representation of the given worded form in the form of inequality is n + 7 ≤ 9
Question 7.
Fifteen is no more than a number t divided by 5.
Answer:
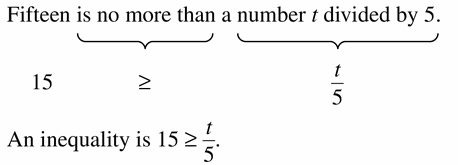
Question 8.
Three times a number w is less than 18.
Answer:
Given,
Three times a number w is less than 18
The representation of the given worded form in the form of inequality is 3w < 18
Question 9.
One-half of a number y is more than 22.
Answer:
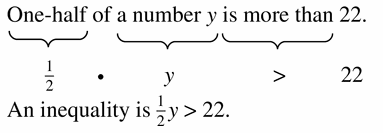
Question 10.
Three is less than the sum of a number s and 4.
Answer:
Given,
Three is less than the sum of a number s and 4
The representation of the given worded form in the form of inequality is 3 < s + 4
Question 11.
Thirteen is at least the difference between a number v and 1.
Answer:
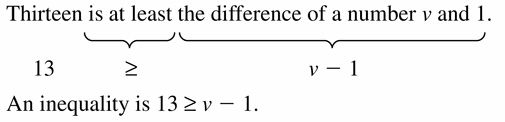
Question 12.
Four is no less than the quotient of a number x and 2.
Answer:
Given,
Four is no less than the quotient of a number x and 2
The representation of the given worded form in the form of inequality is 4 > x ÷ 2
Question 13.
MODELING WITH MATHEMATICS
On a fishing trip, you catch two fish. The weight of the first fish is shown. The second fish weighs at least 0.5 pound more than the first fish. Write an inequality that represents the possible weights of the second fish.

Answer:
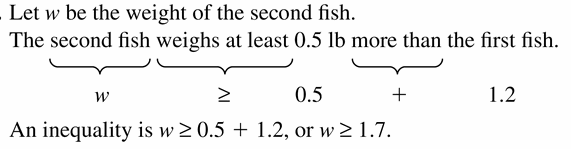
Question 14.
MODELING WITH MATHEMATICS
There are 430 people in a wave pool. Write an inequality that represents how many more people can enter the pool.

Answer:
Given,
There are 430 people in a wave pool.
430 + x = 600
x is the number of more people that can enter the pool.
In Exercises 15–24, tell whether the value is a solution to the inequality.
Question 15.
r + 4 > 8; r = 2
Answer:

Question 16.
5 – x < 8; x = -3
Answer:
Given,
5 – x < 8
x = -3
5 – ( -3 ) < 8
5 + 3 < 8
8 < 8
x = -3 is not a solution to the given inequality
Question 17.
3s ≤ 19; s = -6
Answer:

Question 18.
17 ≥ 2y ; y = 7
Answer:
Given,
17 ≥ 2y
y = 7
17 ≥ 2 ( 7 )
17 ≥ 14
y = 7 is a solution to the given inequality.
Question 19.
-1 > –\(\frac{x}{2}\); x = 3
Answer:
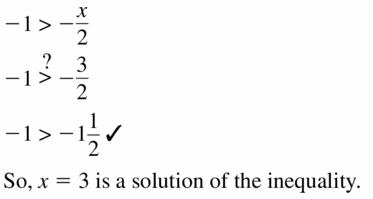
Question 20.
–\(\frac{4}{z}\) ≥ 3; z = 2
Answer:
Given,
–\(\frac{4}{z}\) ≥ 3
z = 2
–\(\frac{4}{2}\) ≥ 3
-2 ≥ 3
z = 2 is not a solution to the given inequality
Question 21.
14 ≥ -2n + 4; n = -5
Answer:
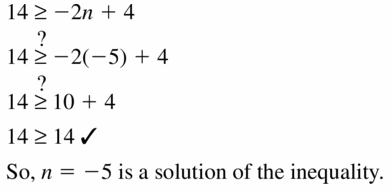
Question 22.
-5 ÷ (2s) < -1; s = 10
Answer:
Given,
-5 ÷ ( 2s ) < -1
s = 10
-5 ÷ 2 ( 10 ) < -1
-5 ÷ 20 < -1
–\(\frac{1}{4}\) < -1
\(\frac{1}{4}\) < 1
1 < 4
s = 10 is a solution to the given inequality
Question 23.
20 ≤ \(\frac{10}{2z}\) + 20; z = 5
Answer:
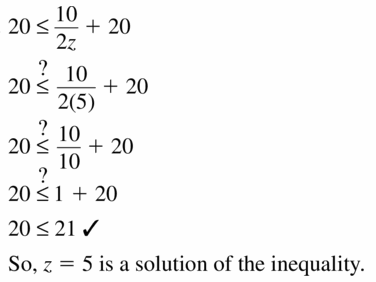
Question 24.
\(\frac{3m}{6}\) – 2 > 3; m = 8
Answer:
Given,
\(\frac{3m}{6}\) – 2 > 3
m = 8
\(\frac{3 × 8}{6}\) > 3 + 2
4 3 + 2
4 > 5
m = 8 is not a solution to the given inequality
Question 25.
MODELING WITH MATHEMATICS
The tallest person who ever lived was approximately 8 feet 11 inches tall.
a. Write an inequality that represents the heights of every other person who has ever lived.
b. Is 9 feet a solution of the inequality? Explain.

Question 26.
DRAWING CONCLUSIONS
The winner of a weight-lifting competition bench-pressed 400 pounds. The other competitors all bench-pressed at least 23 pounds less.
a. Write an inequality that represents the weights that the other competitors bench-pressed.
Answer:
The winner of a weight-lifting competition bench-pressed 400 pounds. The other competitors all bench-pressed at least 23 pounds less.
x be the number of pounds that all the other competitors bench-pressed
The inequality that represents the weights that the other competitors bench-pressed is x + 23 ≤ 400
b. Was one of the other competitors able to bench-press 379 pounds? Explain.
Answer:
The inequality that represents the weights that the other competitors bench-pressed is
x + 23 ≤ 400
x ≤ 400 – 23
x ≤ 377 pounds
Hence, one of the other competitors won’t be able to bench-press 379 pounds
ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in determining whether 8 is in the solution set of the inequality.
Question 27.

Answer:

Question 28.

Answer:
Given,
\(\frac{1}{2}\)x + 2 ≤ 6
x = 8
\(\frac{1}{2}\) × 8 ≤ 6 – 2
\(\frac{8}{2}\) ≤ 4
4 ≤ 4
8 is a solution set of the given inequality
In Exercises 29–36, graph the inequality.
Question 29.
x ≥ 2
Answer:
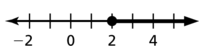
Question 30.
z ≤ 5
Answer:
Given,
z ≤ 5

Question 31.
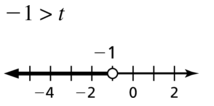
-1 > t
Answer:
Question 32.
-2 < w
Answer:
-2 < w
w > -2
The representation of the given inequality in the number line is

Question 33.
v ≤ -4
Answer:
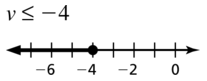
Question 34.
s < 1
Answer:
Given,
s < 1

Question 35.
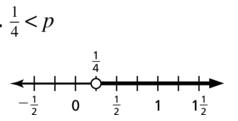
\(\frac{1}{4}\) < p
Answer:
Question 36.
r ≥ -| 5 |
Answer:
Given,
r ≥ – | 5 |
| x | = x for x > 0
| x | = -x for x < 0
r ≥ -5 ( or ) r ≥ 5
The representation of the given inequalities in the number line is

In Exercises 37–40, write and graph an inequality for the given solution set.
Question 37.
{x | x < 7}
Answer:
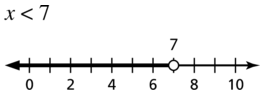
Question 38.
{n | n ≥ -2}
Answer:
Given,
{n | n ≥ -2}
n ≥ -2
The representation of the given inequality in the number line is:

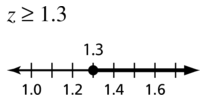
Question 39.
{z | 1.3 ≤ z}
Answer:
Question 40.
{w | 5.2 > w}
Answer:
Given,
{w | 5.2 > w}
5.2 > w
w < 5.2
We can say that 5.2 lies between 5 and 6

In Exercises 41–44, write an inequality that represents the graph.
Question 41.
![]()
Answer:
![]()
Question 42.
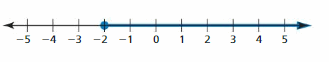
Answer:
We can say that the marked line started from -2 and ended at the last value on the right side of the number line.
x ≥ -2
Question 43.
![]()
Answer:
![]()
Question 44.
![]()
Answer:
We can say that the marked line started from -1 excluding – and continued till the end of the number line on the left side of the number line.
x < -1
Question 45.
ANALYZING RELATIONSHIPS
The water temperature of a swimming pool must be no less than 76°F. The temperature is currently 74°F. Which graph correctly shows how much the temperature needs to increase? Explain your reasoning.
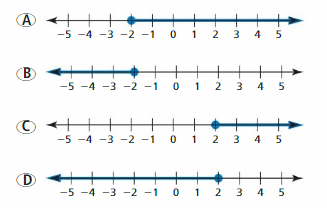
Answer:
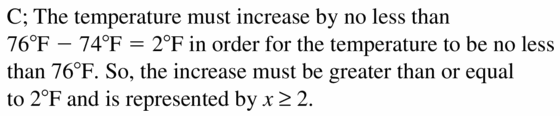
Question 46.
MODELING WITH MATHEMATICS
According to state law for vehicles traveling on state roads, the maximum total weight of a vehicle and its contents depends on the number of axles on the vehicle. For each type of vehicle, write and graph an inequality that represents the possible total weights w (in pounds) of the vehicle and its contents.

Answer:
Let, w be the total weight of the vehicle and its contents
For the 2 axles vehicle, if the maximum weight is 40,000 lb and w is the possible total weight of the vehicle and its contents, then
w < 40,000

For the 3 axles vehicle, if the maximum weight is 60,000 lb and w is the possible total weight of the vehicle and its contents, then
w < 60,000

For the 4 axles vehicle, if the maximum weight is 80,000 lb and w is the possible total weight of the vehicle and its contents, then
w < 80,000

Question 47.
PROBLEM-SOLVING
The Xianren Bridge is located in Guangxi Province, China. This arch is the world’s longest natural arch, with a length of 400 feet. Write and graph an inequality that represents the lengths ℓ (in inches) of all other natural arches.

Answer:
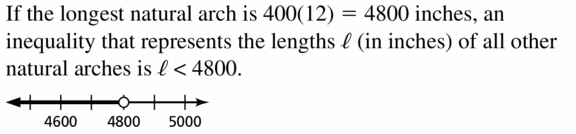
Question 48.
THOUGHT-PROVOKING
A student works no more than 25 hours each week at a part-time job. Write an inequality that represents how many hours the student can work each day.
Answer:
Given,
A student works no more than 25 hours each week at a part-time job.
Let the number of days that students work each week be x
x < 25
1 week = 7 days
7x < 25
x < \(\frac{25}{7}\)
x < 3.5

Question 49.
WRITING
Describe a real-life situation modeled by the inequality 23 + x ≤ 31.
Answer:

Question 50.
HOW DO YOU SEE IT?
The graph represents the known melting points of all metallic elements (in degrees Celsius). ![]()
a. Write an inequality represented by the graph.
Answer:
We can say that the marked line started from -38.87 and continued till the end of the right line of the number line
x ≥ -38.87
b. Is it possible for a metallic element to have a melting point of -38.87°C? Explain.
Answer:
Given,
![]()
From the above graph,
The starting point is -38.87
Yes, it is possible for a metallic element to have a melting point of -38.87°C.
Question 51.
DRAWING CONCLUSIONS
A one-way ride on a subway costs $0.90. A monthly pass costs $24. Write an inequality that represents how many one-way rides you can buy before it is cheaper to buy the monthly pass. Is it cheaper to pay the one-way fare for 25 rides? Explain.

Answer:

Question 52.
MAKING AN ARGUMENT
The inequality x ≤ 1324 represents the weights (in pounds) of all mako sharks ever caught using a rod and reel. Your friend says this means no one using a rod and reel has ever caught a mako shark that weighs 1324 pounds. Your cousin says this means someone using a rod and reel has caught a mako shark that weighs 1324 pounds. Who is correct? Explain your reasoning.
Answer:
Given,
x ≤ 1324
The meaning of inequality is the value of x is less than or equal to 1324 pounds
Your friend says this means no one using a rod and reel has ever caught a mako shark that weighs 1324 pounds
The statement of your friend is wrong
Your cousin says this means someone using a rod and reel has caught a mako shark that weighs 1324 pounds
The statement of your cousin is correct.
Your cousin is correct
Question 53.
CRITICAL THINKING
Describe a real-life situation that can be modeled by more than one inequality.
Answer:

Question 54.
MODELING WITH MATHEMATICS
In 1997, Superman’s cape from the 1978 movie Superman was sold at an auction. The winning bid was $17,000. Write and graph an inequality that represents the amounts all the losing bids.
Answer:
In 1997, Superman’s cape from the 1978 movie Superman was sold at an auction.
The winning bid was $17,000.
The winning bid was $17,000.
The inequality that represents the amount of all losing bids is
x < 17,000
![]()
MATHEMATICAL CONNECTIONS
In Exercises 55–58, write an inequality that represents the missing dimension x.
Question 55.
The area is less than 42 square meters.
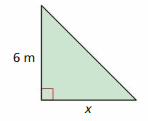
Answer:
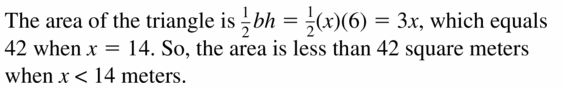
Question 56.
The area is greater than or equal to 8 square feet.
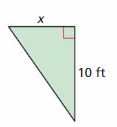
Answer:
We can say that the given figure is a Right-angled triangle
The area of the triangle = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × x × 10
= 5x
It is given that the area of the triangle is greater than or equal to 8 square feet
5x ≥ 8 square feet
x ≥ \(\frac{8}{5}\)
Question 57.
The area is less than 18 square centimeters.
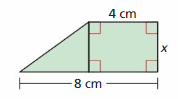
Answer:
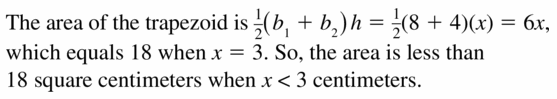
Question 58.
The area is greater than 12 square inches.
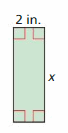
Answer:
Given,
The area is greater than 12 square inches.
The area of the rectangle = Length × Width
2x > 12
x > 12/2
x > 6
Question 59.
WRITING
A runner finishes a 200-meter dash in 35 seconds. Let r represent any speed (in meters per second) faster than the runner’s speed.
a. Write an inequality that represents r. Then graph the inequality.
b. Every point on the graph represents a speed faster than the runner’s speed. Do you think every point could represent the speed of a runner? Explain.
Answer:

Maintaining Mathematical Proficiency
Solve the equation. Check your solution.(Section 1.1)
Question 60.
x + 2 = 3
Answer:
Given,
x + 2 = 3
x = 3 – 2
x = 1
Question 61.
y – 9 = 5
Answer:
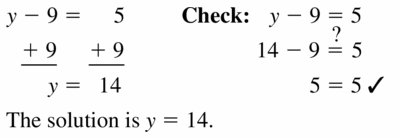
Question 62.
6 = 4 + y
Answer:
Given,
6 = 4 + y
6 – 4 = y
2 = y
y = 2
Question 63.
-12 = y – 11
Answer:

Solve the literal equation for x.(Section 1.5)
Question 64.
v = x • y • z
Answer:
v = x ⋅ y ⋅ z
x = \(\frac{v}{yz}\)
Question 65.
s = 2r + 3x
Answer:
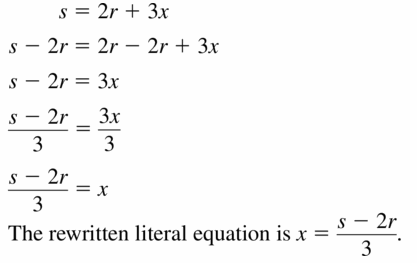
Question 66.
w = 5 + 3(x – 1)
Answer:
Given,
w = 5 + 3 ( x – 1 )
w = 5 + 3 ( x ) – 3 ( 1 )
w = 5 + 3x – 3
w = 3x + 2
3x = w – 2
x = \(\frac{w – 2}{3}\)
Question 67.
n = \(\frac{2x + 1}{2}\)
Answer:
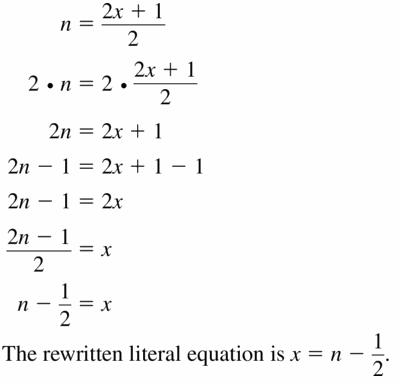
Lesson 2.2 Solving Inequalities Using Addition or Subtraction
Essential Question
How can you use addition or subtraction to solve an inequality?
EXPLORATION 1
Quarterback Passing Efficiency
Work with a partner.
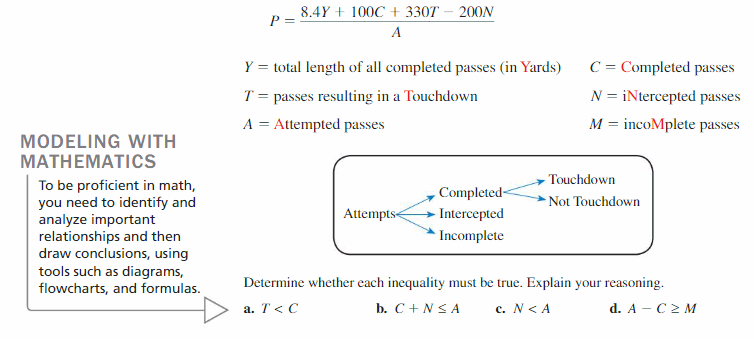
The National Collegiate Athletic Association (NCAA) uses the following formula to rank the passing efficiencies P of quarterbacks.
Answer:
The formula used to rank the passing efficiencies P of the quarterbacks is:

Y = 8.4
C = 100
T = 330
N = 200
A = 1
a) T < C
= 330 < 100
Hence, the given inequality is not true.
b) C + N ≤ A
= ( 100 + 200 ) ≤ 1
= 300 ≤ 1
Hence, the given inequality is not true.
c) N < A
= 200 < 1
Hence, the given inequality is not true.
d) A – C ≥ M
M = C – N
A-C ≥ C – N
( 1 – 100 ) ≥ ( 100 – 200 )
= -99 ≥ -100
= 99 ≥ 100
Hence, the given inequality is not true.
EXPLORATION 2
Finding Solutions of Inequalities
Work with a partner.
Use the passing efficiency formula to create a passing record that makes each inequality true. Record your results in the table. Then describe the values of P that make each inequality true.

a. P < 0
b. P + 100 ≥ 250
c. P – 250 > -80
Answer:

The formula for passing efficiency is:
![]()
a) P < 0
To make P < 0,
The value of A or any of the values of the numerator must be less than 0
b) P + 100 ≥ 250
P ≥ 250 – 100
P ≥ 150
c ) P – 250 > -80
P > -80 + 250
P > 170
Communicate Your Answer
Question 3.
How can you use addition or subtraction to solve an inequality?
Answer:
If you want to add or subtract from one side of the equation, you have to perform the same operation on the other side of the equation. When solving inequalities by adding or subtracting, our aim is to have the variable on its own.
Question 4.
Solve each inequality.
a. x + 3 < 4 b. x – 3 ≥ 5 c. 4 > x – 2
d. -2 ≤ x + 1
Answer:
a) x + 3 < 4
x < 4 – 3
x < 1
b) x – 3 ≥ 5
x ≥ 5 + 3
x ≥ 8
c) 4 > x – 2
4 + 2 > x
6 > x
x < 6
d) -2 ≤ x + 1
-2 – 1 ≤ x
-3 ≤ x
x ≥ -3
2.2 Lesson
Monitoring Progress
Solve the inequality. Graph the solution.
Question 1.
b – 2 > -9
Answer:
b – 2 > -9
b > -9 + 2
b > -7

Question 2.
m – 3 ≤ 5
Answer:
m – 3 ≤ 5
m ≤ 5 + 3
m ≤ 8

Question 3.
\(\frac{1}{4}\) > y – \(\frac{1}{4}\)
Answer:
\(\frac{1}{4}\) > y – \(\frac{1}{4}\)
\(\frac{1}{4}\) + \(\frac{1}{4}\) > y
\(\frac{1 + 1}{4}\) > y
\(\frac{2}{4}\) > y
\(\frac{1}{2}\) > y
y < \(\frac{1}{2}\)

Solve the inequality. Graph the solution.
Question 4.
k + 5 ≤ -3
Answer:
k + 5 ≤ -3
k ≤ -3 – 5
k ≤ -8

Question 5.
\(\frac{5}{6}\) ≤ z + \(\frac{1}{6}\)
Answer:
\(\frac{5}{6}\) ≤ z + \(\frac{1}{6}\)
\(\frac{5}{6}\) – \(\frac{1}{6}\) ≤ z
\(\frac{5 – 1}{6}\) ≤ z
\(\frac{4}{6}\) ≤ z
\(\frac{2}{3}\) ≤ z
z ≥ \(\frac{2}{3}\)
z ≥ 0.6
z ≥ 1 ( Approx. )

Question 6.
p + 0.7 > -2.3
Answer:
p + 0.7 > -2.3
p > -2.3 – 0.7
p > -3

Monitoring Progress
Question 7.
The microwave oven uses only 1000 watts of electricity. Does this allow you to have both the microwave oven and the toaster plugged into the circuit at the same time? Explain your reasoning.
Answer:
Given,
The microwave oven uses only 1000 watts of electricity.
The toaster consumes less electricity than the microwave oven.
1000 watts of electricity allow you to have both the microwave oven and the toaster plugged into the circuit at the same time.
Solving Inequalities Using Addition or Subtraction 2.2 Exercises
In Exercises 3−6, tell which number you would add to or subtract from each side of the inequality to solve it.
Question 1.
VOCABULARY
why is the inequality x ≤ 6 equivalent to the inequality x – 5 ≤ 6 – 5 ?
Answer:
Question 2.
WRITING
Compare solving equations using addition with solving inequalities using addition.
Answer:
Solving equations and inequalities using addition is very similar. Add the same quantity on every side and the sign between the two sides does not change. It remains the equal sign “=” in the case of equations and the inequality sign in the case of inequalities
Question 3.
k + 11 < -3
Answer:

Question 4.
v – 2 > 14
Answer:
Given,
v – 2 > 14
Add 2 on both sides
v – 2 + 2 > 14 + 2
v > 16
Question 5.
-1 ≥ b – 9
Answer:

Question 6.
-6 ≤ 17 + p
Answer:
Given,
-6 ≤ 17 + p
Add 6 on both sides
-6 + 6 ≤ 17 + 6 + p
0 ≤ 23 + p
-23 ≤ p
p ≥ -23
In Exercises 7−20, solve the inequality. Graph the solution.
Question 7.
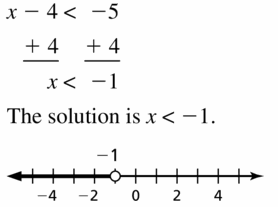
x – 4 < -5
Answer:
Question 8.
1 ≤ s – 8
Answer:
Given,
1 ≤ s – 8
1 + 8 ≤ s – 8 + 8
9 ≤ s
s ≥ 9

Question 9.
6 ≥ m – 1
Answer:
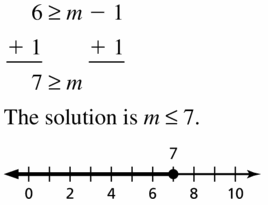
Question 10.
c – 12 > -4
Answer:
Given,
c – 12 > -4
c – 12 + 4 > -4 + 4
c – 8 > 0
c > 0 + 8
c > 8

Question 11.
r + 4 < 5
Answer:
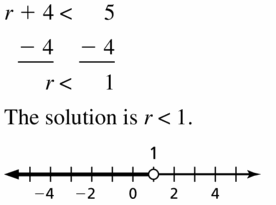
Question 12.
-8 ≤ 8 + y
Answer:
Given,
-8 ≤ 8 + y
-8 + 8 ≤ 8 + 8 + y
0 ≤ 16 + y
-16 ≤ y
y ≥ -16
The representation of the inequality in the number line is

Question 13.
9 + w > 7
Answer:
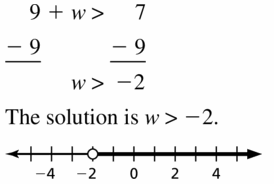
Question 14.
15 ≥ q + 3
Answer:
Given,
15 ≥ q + 3
15 – 15 ≥ q + 3 – 15
0 ≥ q – 12
12 ≥ q
q ≤ 12
The representation of the inequality in the number line is

Question 15.
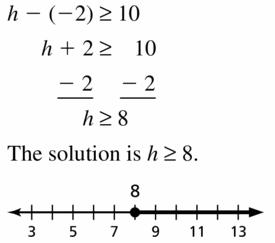
h – (-2) ≥ 10
Answer:
Question 16.
-6 > t – (-13)
Answer:
Given,
-6 > t – ( -13 )
-6 + 6 > t + 13 + 6
0 > t + 19
-19 > t
t < -19
The representation of the inequality in the number line is
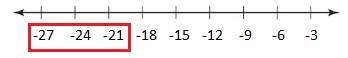
Question 17.
j + 9 – 3 < 8
Answer:
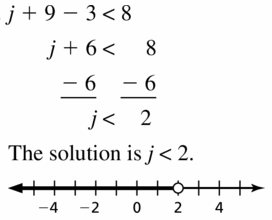
Question 18.
1 – 12 + y ≥ -5
Answer:
Given,
1 – 12 + y ≥ -5
-11 + y ≥ -5
-11 + 5 + y ≥ -5 + 5
6 + y ≥ 0
y ≥ -6
The representation of the inequality in the number line is

Question 19.
10 ≥ 3p – 2p – 7
Answer:
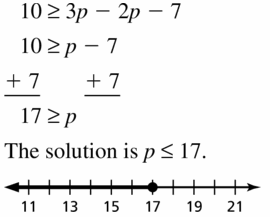
Question 20.
18 – 5z + 6z > 3 + 6
Answer:
Given,
18 – 5z + 6z > 3 + 6
18 + z > 9
18 – 9 + z > 9 – 9
z + 9 > 0
z > -9
The representation of the inequality in the number line is

In Exercises 21−24, write the sentence as an inequality. Then solve the inequality.
Question 21.
A number plus 8 is greater than 11.
Answer:
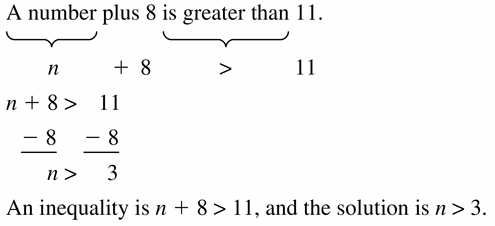
Question 22.
A number minus 3 is at least -5.
Answer:
A number minus 3 is at least -5
Let the number be x
x – 3 ≥ -5
x – 3 + 5 ≥ -5 + 5
x + 2 ≥ 0
x ≥ -2
Question 23.
The difference of a number and 9 is fewer than 4.
Answer:
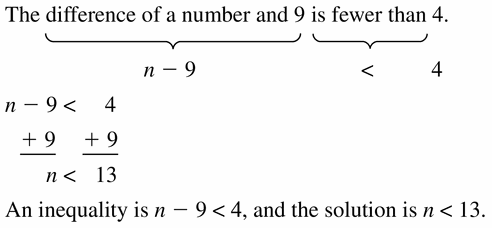
Question 24.
Six is less than or equal to the sum of a number and 15.
Answer:
Six is less than or equal to the sum of a number and 15
Let the number be x
6 ≤ x + 15
6 – 6 ≤ x + 15 – 6
0 ≤ x + 9
-9 ≤ x
x ≥ -9
Question 25.
MODELING WITH MATHEMATICS
You are riding a train. Your carry-on bag can weigh no more than 50 pounds. Your bag weighs 38 pounds.
a. Write and solve an inequality that represents how much weight you can add to your bag.
b. Can you add both a 9-pound laptop and a 5-pound pair of boots to your bag without going over the weight limit? Explain.
Answer:

Question 26.
MODELING WITH MATHEMATICS
You order the hardcover book shown from a website that offers free shipping on orders of $25 or more. Write and solve an inequality that represents how much more you must spend to get free shipping.

Answer:
You order the hardcover book shown from a website that offers free shipping on orders of $25 or more.
The cost of a hardcover book is: $19.76
The amount more money you must spend to get free shipping to be x
x + 19.76 ≥ 25
x + 19.76 – 25 ≥ 25 – 25
x – 5.24 ≥ 0
x ≥ $5.24
ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in solving the inequality or graphing the solution.
Question 27.
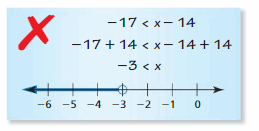
Answer:

Question 28.
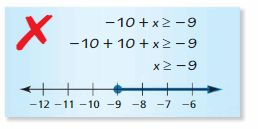
Answer:
Given,
-10 + x ≥ -9
-10 + 9 + x ≥ -9 + 9
-1 + x ≥ 0
x ≥ 1
The representation of the inequality in the number line is

Question 29.
PROBLEM-SOLVING
An NHL hockey player has 59 goals so far in a season. What are the possible numbers of additional goals the player can score to match or break the NHL record of 92 goals in a season?
Answer:
Question 30.
MAKING AN ARGUMENT
In an aerial ski competition, you perform two acrobatic ski jumps. The scores on the two jumps are then added together.
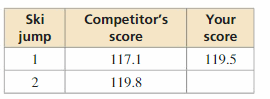
a. Describe the score that you must earn on your second jump to beat your competitor.
Answer:

Let the score of your second acrobatic ski jump be x
We can say that your score must be greater than your competitor’s score to beat your competitor
The inequality that represents the score you must earn on your second jump to beat your competitor is
x > 119.8
b. Your coach says that you will beat your competitor if you score 118.4 points. A teammate says that you only need 117.5 points. Who is correct? Explain.
Answer:

In the 1st acrobatic ski jump,
Your competitor’s score is: 117.1
Your score is: 119.5
If you want to beat your competitor, then you have to score more than 117.1
x > 117.1
It is given that your coach says that you will beat your competitor if you score 118.4 points. A teammate says that you only need 117.5 points
You have to score 118.4 points to beat your competitor
118.4 > 117.1
You have to score 117.5 points to beat your competitor
117.5 > 117.1
Question 31.
REASONING
Which of the following inequalities are equivalent to the inequality x – b < 3, where b is a constant? Justify your answer.
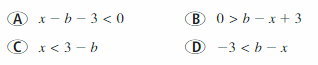
Answer:
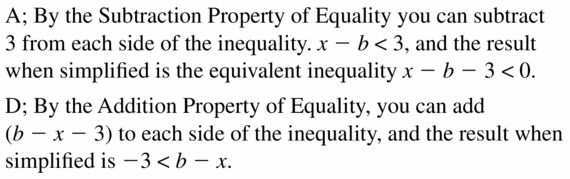
MATHEMATICAL CONNECTIONS
In Exercises 32 and 33, write and solve an inequality to find the possible values of x.
Question 32.
Perimeter < 51.3 inches
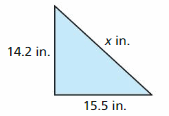
Answer:
The figure is the triangle
The perimeter is the sum of all of the sides
The perimeter of the triangle = 15.5 + 14.2 + x
Perimeter < 51.3 inches
51.3 < 29.7 + x
51.3 – 29.7 < x
21.6 < x
x > 21.6
The value of x is greater than 21.6 inches.
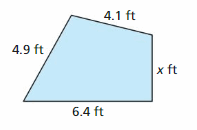
Question 33.
Perimeter ≤ 18.7 feet
Answer:

Question 34.
THOUGHT-PROVOKING
Write an inequality that has the solution shown in the graph. Describe a real-life situation that can be modeled by inequality.
![]()
Answer:
The marked line is starting from 16 and continued till the left end of the number line
The inequality that represents the given number line is:
x ≤ 16
The real-life situation that can be modeled by inequality is “A lift carrying no more than 16 people”.
Question 35.
WRITING
Is it possible to check all the numbers in the solution set of an inequality? When you solve the inequality x – 11 ≥ -3, which numbers can you check to verify your solution? Explain your reasoning.
Answer:

Question 36.
HOW DO YOU SEE IT?
The diagram represents the numbers of students in a school with brown eyes, brown hair, or both.
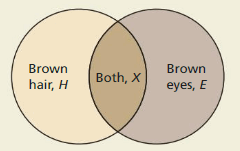
Determine whether each inequality must be true. Explain your reasoning.
a. H ≥ E
b. H + 10 ≥ E
c. H ≥ X
d. H + 10 ≥ X
e. H > X
f. H + 10 > X
Answer:
The spaces occupied by H and E are equal
The spaces occupied by H and E are greater than X
H = E; H > X; E > X
a. H ≥ E
The given inequality is not true
b. H + 10 ≥ E
The given inequality is not true
c. H ≥ X
The given inequality is not true
d. H + 10 ≥ X
The given inequality is not true
e. H > X
The given inequality is true
f. H + 10 > X
The given inequality is true
Question 37.
REASONING
Write and graph an inequality that represents the numbers that are not solutions to each inequality.
a. x + 8 < 14
b. x – 12 ≥ 5.7
Answer:
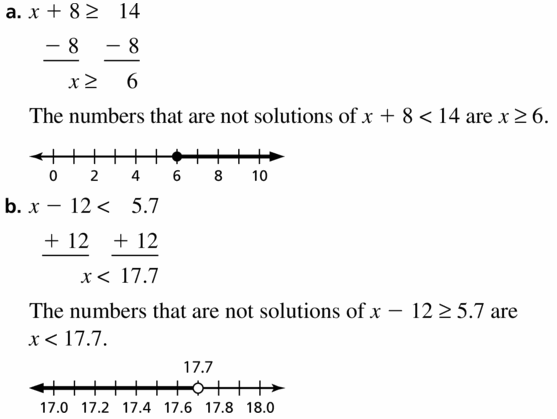
Question 38.
PROBLEM-SOLVING
Use the inequalities c – 3 ≥ d, b + 4 < a + 1, and a – 2 ≤ d – 7 to order a, b, c, and d from least to greatest.
Answer:
The given inequalities are:
A) c – 3 ≥ d
B) b + 4 < a + 1
C) a – 2 ≤ d – 7
Now,
A) c – 3 ≥ d
c ≥ d + 3
B) b + 4 < a + 1
b < a + 1 – 4
b < a – 3
b + 3 < a
a > b + 3
C) a – 2 ≤ d – 7
a ≤ d – 7 + 2
a ≤ d – 5
a + 5 ≤ d
d ≥ a + 5
The order of a, b, c, d from least to greatest is b, a, c, and d
Maintaining Mathematical Proficiency
Find the product or quotient.
Question 39.
7 • (-9)
Answer:
![]()
Question 40.
-11 • (-12)
Answer:
-11 ⋅ ( -12 )
= 11 ⋅ 12
= 132
Question 41.
-27 ÷ (-3)
Answer:
![]()
Question 42.
20 ÷ (-5)
Answer:
20 ÷ ( -5 )
= -20 ÷ 5
= -4
Solve the equation. Check your solution.(Section 1.1)
Question 43.
6x = 24
Answer:

Question 44.
-3y = -18
Answer:
-3y = -18
y = -18 ÷ ( -3 )
y = 6
Question 45.
\(\frac{s}{-8}\) = 13
Answer:

Question 46.
\(\frac{n}{4}\) = -7.3
Answer:
\(\frac{n}{4}\) = -7.3
n = -7.3 × 4
n = -29.2
Lesson 2.3 Solving Inequalities Using Multiplication or Division
Essential Question
How can you use division to solve inequality?
EXPLORATION 1
Writing a Rule
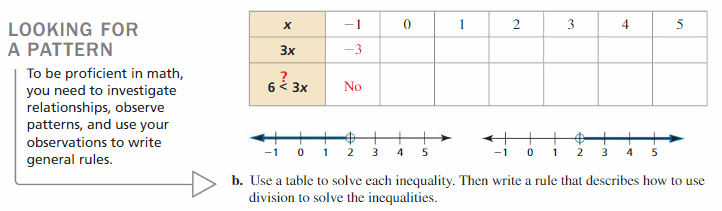
Work with a partner.
a. Copy and complete the table. Decide which graph represents the solution of the inequality 6 < 3x. Write the solution to the inequality.
Answer:
a)
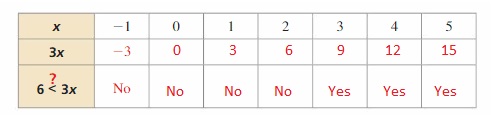
The given number lines are:
![]()
We can say that the expression 6 < 3x will be true if the value of x is greater than 2
From the 2nd number line,
The value of x is greater than 2
b)
6 < 3x
3x > 6
x > 6 ÷ 3
x > 2
x > 2 means x = 3, 4, 5
The value of x is: 3, 4, 5
i. 2x < 4
Answer:
2x < 4
x < 4 / 2
x < 2
x < 2 will be held true if the value of x is -1, 0, 1
ii. 3 ≥ 3x
Answer:
3 ≥ 3x
1 ≥ x
x ≤ 1
We can observe that x ≤ 1 will be held true if the value of the x is -1, 0, 1
iii. 2x < 8
Answer:
2x < 8
x < 8 / 2
x < 4
We can observe that x < 4 will be held true if the value of x is -1, 0, 1, 2, 3
iv. 6 ≥ 3x
Answer:
6 ≥ 3x
So,
6 / 3 ≥ x
2 ≥ x
x ≤ 2
x ≤ 2 will be held true if the value of x is -1, 0, 1, 2
EXPLORATION 2
Writing a Rule
Work with a partner.
a. Copy and complete the table. Decide which graph represents the solution of the inequality 6 < -3x. Write the solution of the inequality.
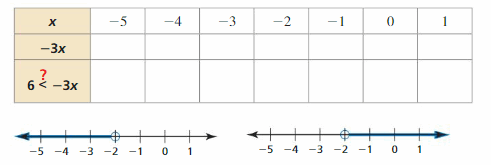
Answer:
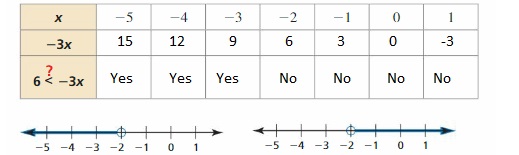
From the given number lines,
The first graph indicates the inequality
x < -2
The second graph indicates the inequality
x > -2
The inequality that represents the table is x < -2
b. Use a table to solve each inequality. Then write a rule that describes how to use division to solve the inequalities.
i. -2x < 4
Answer:
-2x < 4
-x < 4 / 2
-x < 2
x < -2
The values of x for the inequality x < -2 is -5, -4, -3
ii. 3 ≥ -3x
Answer:
3 ≥ -3x
1 ≥ -x
-1 ≥ x
x ≤ -1
The values of x for the inequality x ≤ -1 is -5, -4, -3, -2, -1
iii. -2x < 8
Answer:
-2x < 8
x < -8 /2
x < -4
The values of x for the inequality x < -4 is -5
iv.6 ≥ -3x
Answer:
6 ≥ -3x
6 / ( -3 ) ≥ x
-2 ≥ x
x ≤ -2
The values of x for the inequality x ≤ -2 is -5, -4, -3, -2
Communicate Your Answer
Question 3.
How can you use division to solve inequality?
Answer:
Division Property of Inequality:
If you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number.
Question 4.
Use the rules you wrote in Explorations 1(b) and 2(b) to solve each inequality.
a. 7x < -21
b. 12 ≤ 4x
c. 10 < -5x d. -3x ≤ 0
Answer:
a. 7x < -21
Answer:
7x < -21
x < -21/7
x < -3
b. 12 ≤ 4x
Answer:
12 ≤ 4x
12 / 4 ≤ x
3 ≤ x
x ≥ 3
c. 10 < -5x
Answer:
10 < -5x
10 / -5 < x
2 < x
x > 2
d. -3x ≤ 0
Answer:
-3x ≤ 0
x ≤ 0 / -3
x ≤ 0
2.3 Lesson
Monitoring Progress Solve the inequality. Graph the solution.
Question 1.
\(\frac{n}{7}\) ≥ -1
Answer:
\(\frac{n}{7}\) ≥ -1
n ≥ -1 ( 7 )
n ≥ -7
The representation of the inequality in the number line is

Question 2.
-6.4 ≥ \(\frac{1}{5}\)w
Answer:
-6.4 ≥ \(\frac{1}{5}\)w
-6.4 ( 5 ) ≥ w
-32 ≥ w
w ≤ -32
The representation of the inequality in the number line is

Question 3.
4b ≥ 36
Answer:
4b ≥ 36
b ≥ 36 / 4
b ≥ 9
The representation of the inequality in the number line is

Question 4.
-18 > 1.5q
Answer:
-18 > 1.5q
-18 / 1.5 > q
-180 / 15 > q
-12 > q
q < -12
The representation of the inequality in the number line is

Monitoring Progress
Solve the inequality. Graph the solution.
Question 5.
\(\frac{p}{-4}\) < 7
Answer:
\(\frac{p}{-4}\) < 7
–\(\frac{p}{4}\) < 7
-p < 7 ( 4 )
-p < 28
p < -28
The representation of the inequality in the number line is
![]()
Question 6.
\(\frac{x}{-5}\) ≤ -5
Answer:
\(\frac{x}{-5}\) ≤ -5
–\(\frac{x}{5}\) ≤ -5
\(\frac{x}{5}\) ≤ 5
x ≤ 5 ( 5 )
x ≤ 25
The representation of the inequality in the number line is
![]()
Question 7.
-1 ≥ –\(\frac{1}{10}\)z
Answer:
-1 ≥ –\(\frac{1}{10}\)z
1 ≥ \(\frac{1}{10}\)z
1 ( 10 ) ≥ z
10 ≥ z
z ≤ 10
The representation of the inequality in the number line is

Question 8.
-9m > 63
Answer:
-9m > 63
m > -63 / 9
m > -7
The representation of the inequality in the number line is

Question 9.
-2r ≥ -22
Answer:
-2r ≥ -22
2r ≥ 22
r ≥ 22 / 2
r ≥ 11
The representation of the inequality in the number line is

Question 10.
-0.4y ≥ -12
Answer:
-0.4y ≥ -12
0.4y ≥ 12
y ≥ 12 / 0.4
y ≥ 120 / 4
y ≥ 30
The representation of the inequality in the number line is

Question 11.
You have at most $3.65 to make copies. Each copy costs $0.25. Write and solve an inequality that represents the number of copies you can make.
Answer:
You have at most $3.65 i.e., you have a maximum of only $3.65 to make copies and it is also given that each copy costs $0.25.
The additional cost to make the copies be $x
The total cost = x + 0.25
The total cost won’t be greater than 3.65
The inequality that represents the number of copies you can make is x + 0.25 ≤ 3.65
Question 12.
The maximum speed limit for a school bus is 55 miles per hour. Write and solve an inequality that represents the number of hours it takes to travel 165 miles in a school bus.
Answer:
Given,
The maximum speed limit for a school bus is 55 miles per hour.
x be the number of hours
The inequality that represents the number of hours it takes to travel 165 miles in a school bus is
55x ≥ 165
x ≥ 165 / 55
x ≥ 3
Solving Inequalities Using Multiplication or Division 2.3 Exercises
In Exercises 3–10, solve the inequality. Graph the solution.
Vocabulary and Core Concept Check
Question 1.
WRITING
Explain how solving 2x < -8 is different from solving -2x < 8
Answer:
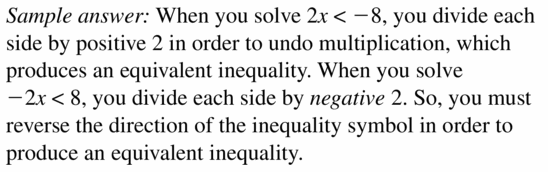
Question 2.
OPEN-ENDED
Write an inequality that is solved using the Division property of Inequality where the inequality symbol needs to be reversed.
Answer:
The required inequality is -6 < 3x
Using the Division Property of Inequality,
-6 / 3 < ( 3 / 3 )x
-2 < x
x > -2
Question 3.
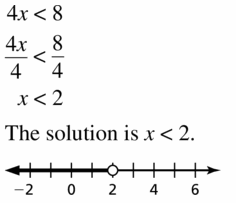
4x < 8
Answer:
Question 4.
3y ≤ -95.
Answer:
Given,
3y ≤ -95
y ≤ -95 / 3
y ≤ -31.6
y ≤ -32 [ Approximate value ]
The representation of the inequality in the number line is

Question 5.
-20 ≤ 10n
Answer:
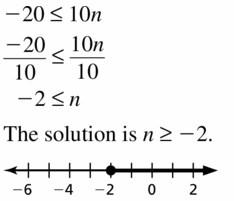
Question 6.
35 < 7t
Answer:
Given,
35 < 7t
35 / 7 < t
5 < t
t > 5
The representation of the inequality in the number line is

Question 7.
\(\frac{x}{2}\) > -2
Answer:
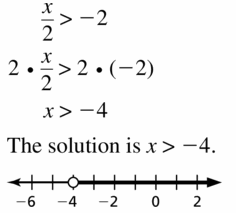
Question 8.
\(\frac{a}{4}\) < 10.2
Answer:
Given,
\(\frac{a}{4}\) < 10.2
a < 10.2 ( 4 )
a < 40.8
a < 40 [ Approximate value ]
The representation of the inequality in the number line is
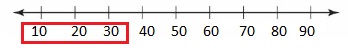
Question 9.
20 ≥ \(\frac{4}{5}\)w
Answer:

Question 10.
-16 ≤ \(\frac{8}{3}\)t
Answer:
-16 ≤ \(\frac{8}{3}\)t
-16 ( 3) ≤ 8t
-48 ≤ 8t
-48 / 8 ≤ t
-6 ≤ t
t ≥ -6

In Exercises 11–18, solve the inequality. Graph the solution.
Question 11.
-6t < 12
Answer:
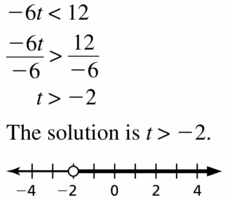
Question 12.
-9y > 9
Answer:
-9y > 9
y > -9 / 9
y > -1

Question 13.
-10 ≥ -2z
Answer:

Question 14.
-15 ≤ -3c
Answer:
-15 ≤ -3c
15 ≤ 3c
15 / 3 ≤ c
5 ≤ c
c ≥ 5

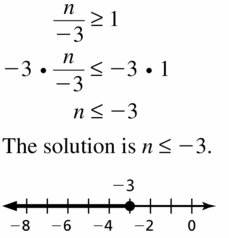
Question 15.
\(\frac{n}{-3}\) ≥ 1
Answer:
Question 16.
\(\frac{w}{-5}\) ≤ 16
Answer:
\(\frac{w}{-5}\) ≤ 16
w ≤ -16 ( 5 )
w ≤ -80

Question 17.
-8 < –\(\frac{1}{4}\)m
Answer:

Question 18.
-6y > –\(\frac{2}{3}\)
Answer:
-6 > –\(\frac{2}{3}\)y
6 > \(\frac{2}{3}\)y
6 ( 3 ) > 2y
18 > 2y
18 / 2 > y
9 > y
y < 9

Question 19.
MODELING WITH MATHEMATICS
You have $12 to buy five goldfish for your new fish tank. Write and solve an inequality that represents the prices you can pay per fish.
Answer:

Question 20.
MODELING WITH MATHEMATICS
A weather forecaster predicts that the temperature in Antarctica will decrease by 8°F each hour for the next 6 hours. Write and solve an inequality to determine how many hours it will take for the temperature to drop at least 36°F.
Answer:
A weather forecaster predicts that the temperature in Antarctica will decrease by 8°F each hour for the next 6 hours.
Let the number of hours that will take to drop the temperature be x
8x ≥ 36
x ≥ 36 / 8
x ≥ 4.5 hours
USING TOOLS
In Exercises 21–26, solve the inequality. Use a graphing calculator to verify your answer.
Question 21.
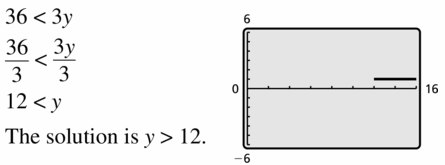
36 < 3y
Answer:
Question 22.
17v ≥ 51
Answer:
17v ≥ 51
v ≥ 51 / 17
v ≥ 3

Question 23.
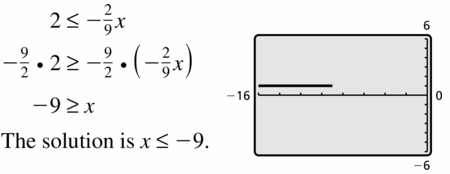
2 ≤ –\(\frac{2}{9}\)x
Answer:
Question 24.
4 > \(\frac{n}{-4}\)
Answer:
4 > \(\frac{n}{-4}\)
4 ( -4 ) > n
-16 > n
n < -16

Question 25.
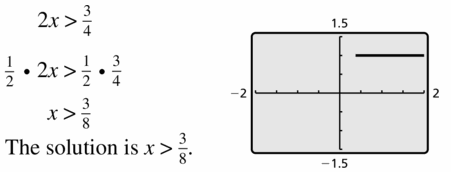
2x > \(\frac{3}{4}\)
Answer:
Question 26.
1.1y < 4.4
Answer:
1.1y < 4.4
\(\frac{11}{10}\)y > \(\frac{44}{10}\)
y > \(\frac{10 × 44}{11 × 10}\)
y > 4

ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in solving the inequality.
Question 27.

Answer:
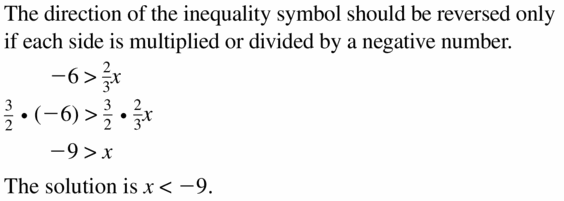
Question 28.

Answer:
-4y ≤ -32
4y ≤ 32
y ≤ 32 /4
y ≤ 8
Question 29.
ATTENDING TO PRECISION
You have $700 to buy a new carpet for your bedroom. Write and solve an inequality that represents the costs per square foot that you can pay for the new carpet. Specify the units of measure in each step.
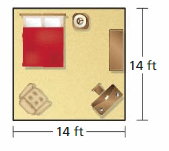
Answer:
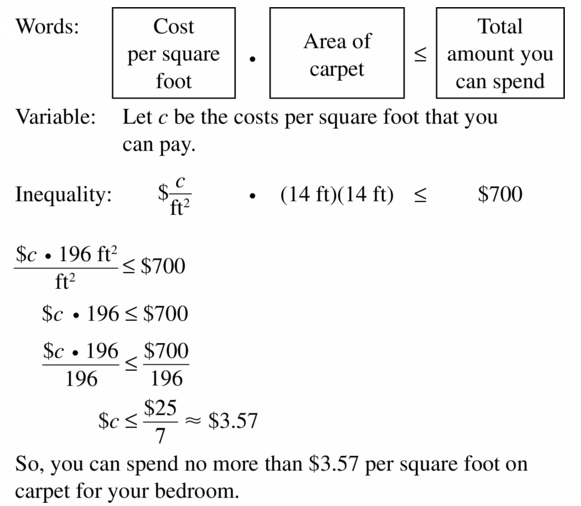
Question 30.
HOW DO YOU SEE IT?
Let m > 0. Match each inequality with its graph. Explain your reasoning.
Answer:
a. \(\frac{x}{m}\) < -1
\(\frac{1}{m}\) < -1
1 < -m
-1 < m
m > -1
From the number lines, D) represents the required number line for this inequality
b. \(\frac{x}{m}\) > 1
x > m
1 > m
m < 1
From the number lines, B) represents the required number line for this inequality
c. \(\frac{x}{m}\) < 1
x < m
1 < m
m > 1
From the number lines, A) represents the required number line for this inequality
d.
–\(\frac{x}{m}\) < 1
-x < -m
x < m
1 < m
m > 1
From the number lines, A) represents the required number line for this inequality
Question 31.
MAKING AN ARGUMENT
You run for 2 hours at a speed no faster than 6.3 miles per hour.
a. Write and solve an inequality that represents the possible numbers of miles you run.
b. A marathon is approximately 26.2 miles. Your friend says that if you continue to run at this speed, you will not be able to complete a marathon in less than 4 hours. Is your friend correct? Explain.
Answer:

Question 32.
THOUGHT-PROVOKING
The inequality
\(\frac{x}{4}\) ≤ 5 has a solution of x = p. Write a second inequality that also has a solution of x = p.
Answer:
\(\frac{x}{4}\) ≤ 5
It is given that the given inequality has a solution of x = p
The second inequality that also has a second solution of x = p is:
\(\frac{x}{4}\) ≤ 5
x ≤ 5 ( 4 )
x ≤ 20
Question 33.
PROBLEM-SOLVING
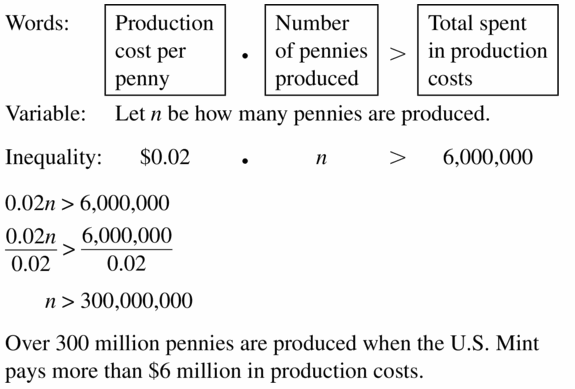
The U.S. Mint pays $0.02 to produce every penny. How many pennies are produced when the U.S. Mint pays more than $6 million in production costs?
Answer:
Question 34.
REASONING
Are x ≤ \(\frac{2}{3}\) and -3x ≤ -2 equivalent? Explain your reasoning.
Answer:
The given inequalities are -3x ≤ -2 and x ≤ \(\frac{2}{3}\)
x ≤ \(\frac{2}{3}\)
3x ≤ 2
-3x ≤ -2
3x ≤ 2
Two inequalities are equivalent.
Question 35.
ANALYZING RELATIONSHIPS
Consider the number line shown.

a. Write an inequality relating A and B.
b. Write an inequality relating -A and -B.
c. Use the results from parts (a) and (b) to explain why the direction of the inequality symbol must be reversed when multiplying or dividing each side of an inequality by the same negative number.
Answer:

Question 36.
REASONING
Why might solving the inequality \(\frac{4}{x}\) ≥ 2 by multiplying each side by x lead to an error? (Hint: Consider x > 0 and x < 0.)
Answer:
\(\frac{4}{x}\) ≥ 2
4 ≥ 2x
4 / 2 ≥ x
2 ≥ x
x ≤ 2
It is given that to consider x > 0 and x < 0 i.e., x as a positive number and a negative number
Multiply the given inequality by x on both sides and consider x as positive
4x ≥ 2x²
4x / 2 ≥ x²
2x / x ≥ x
2 ≥ x
x ≤ 2
Multiply the given inequality by x on both sides and consider x as negative
-4x ≥ -2x²
4x / 2 ≥ x²
2x ≥ x²
2x / x ≥ x
2 ≥ x
x ≤ 2
Question 37.
MATHEMATICAL CONNECTIONS
The radius of a circle is represented by the formula r = \(\frac{C}{2π}\). Write and solve an inequality that represents the possible circumferences C of the circle.
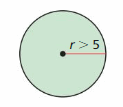
Answer:

Question 38.
CRITICAL THINKING
A water-skiing instructor recommends that a boat pulling a beginning skier has a speed less than 18 miles per hour. Write and solve an inequality that represents the possible distances d (in miles) that a beginner can travel in 45 minutes of practice time.
Answer:
A water-skiing instructor recommends that a boat pulling a beginning skier has a speed less than 18 miles per hour
The given speed is in terms of miles per hour
The time should also be in hours
But the given time is in minutes
60 minutes = 1 hour
45 minutes = \(\frac{45}{60}\) hours
= \(\frac{3}{4}\) hours
It is also given that the distance is d
Speed = \(\frac{Distance}{Time}\)
Distance = Speed × Time
d < 18 ( \(\frac{3}{4}\) )
d < \(\frac{18 × 3}{4}\)
d < \(\frac{54}{4}\)
d < \(\frac{27}{2}\)
d < 13.5 miles
Question 39.
CRITICAL THINKING
A local zoo employs 36 people to take care of the animals each day. At most, 24 of the employees work full time. Write and solve an inequality that represents the fraction of employees who work part-time. Graph the solution. Maintaining Mathematical Proficiency Solve the equation. Check your solution. (Section 1.2 and Section 1.3)
Answer:

Question 40.
5x + 3 = 13
Answer:
5x + 3 = 13
5x = 13 – 3
5x = 10
x = 10 / 2
x = 5
Question 41.
\(\frac{1}{2}\)y – 8 = -10
Answer:

Question 42.
-3n + 2 = 2n – 3
Answer:
-3n + 2 = 2n – 3
-3n – 2n = -3 – 2
-5n = -5
5n = 5
n = 5 / 5
n = 1
Question 43.
\(\frac{1}{2}\)z + 4 = \(\frac{5}{2}\)z – 8 Tell which number is greater.
Answer:
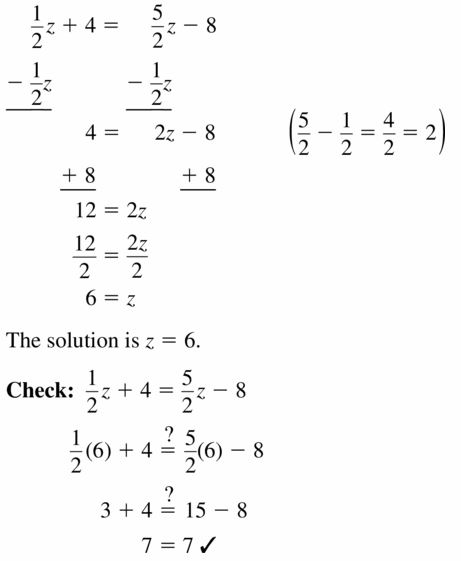
Question 44.
0.8, 85%
Answer:
x% = \(\frac{x}{100}\)
We can rewrite 0.8 as 0.80 since both 0.8 and 0.80 are the same
85% = \(\frac{85}{100}\)
0.8 = \(\frac{80}{100}\)
By comparison, we can get
0.8 is less than 85%
0.8 < 85%
Question 45.
\(\frac{16}{30}\), 50%
Answer:
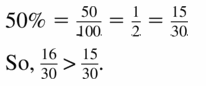
Question 46.
120%, 0.12
Answer:
x% = \(\frac{x}{100}\)
120% = \(\frac{120}{100}\)
0.12 = \(\frac{12}{100}\)
By comparison, we can get
120% is greater than 0.12
120% > 0.12
Question 47.
60%, \(\frac{2}{3}\)
Answer:
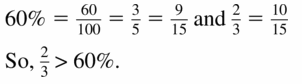
Lesson 2.4 Solving Multi-step Inequalities
Essential Question
How can you solve a multi-step inequality?
EXPLORATION 1
Solving a Multi-Step Inequality
Work with a partner.
• Use what you already know about solving equations and inequalities to solve each multi-step inequality. Justify each step.
• Match each inequality with its graph. Use a graphing calculator to check your answer.
a. 2x + 3 ≤ x + 5
b. -2x + 3 > x + 9
c. 27 ≥ 5x + 4x
d. -8x + 2x – 16 < -5x + 7x
e. 3(x – 3) – 5x > -3x – 6
f. -5x – 6x ≤ 8 – 8x – x

Answer:
The given inequalities are:
a. 2x + 3 ≤ x + 5
b. -2x + 3 > x + 9
c. 27 ≥ 5x + 4x
d. -8x + 2x – 16 < -5x + 7x
e. 3(x – 3) – 5x > -3x – 6
f. -5x – 6x ≤ 8 – 8x – x
The given graphing calculators are:

Now,
From the graphing calculators, we can observe that the graph is divided into 4 parts.
The first part indicates +x
The second part indicates -x
Now,
a.
The given inequality is:
2x + 3 ≤ x + 5
So,
2x – x ≤ 5 – 3
x ≤ 2
Hence, from the above,
We can conclude that the solution to the given inequality is x ≤ 2
The graph B) matches the solution of the given inequality
b.
The given inequality is:
-2x + 3 > x + 9
So,
-2x – x > 9 -3
-3x > 6
x > -6 / 3
x > -2
The solution to the given inequality is x > -2
The graph C) matches the solution of the given inequality
c. 27 ≥ 5x + 4x
27 ≥ 9x
27 / 9 ≥ x
3 ≥ x
x ≤ 3
We can conclude that the solution to the given inequality is x ≤ 3
Graph E) matches the solution of the given inequality.
d. -8x + 2x – 16 < -5x + 7x
-6x – 16 < 2x
-6x – 2x < 16
-8x < 16
x < -16 / 8
x < -2
We can conclude that the solution to the given inequality is x < -2
Graph A) matches the solution of the given inequality
e. 3(x – 3) – 5x > -3x – 6
3 ( x ) – 3 ( 3 ) – 5x > -3x – 6
3x – 9 – 5x > -3x – 6
-2x – 9 > -3x – 6
-2x + 3x > -6 + 9
x > 3
We can conclude that the solution to the given inequality is x > 3
The graph D) matches the solution of the given inequality
f. -5x – 6x ≥ 8 – 8x – x
-11x ≥ 8 – 9x
-11x + 9x ≥ 8
-2x ≥ 8
x ≥ -8 / 2
x ≥ -4
The solution to the given inequality is x ≥ -4
The graph F) matches the solution of the given inequality
Question 2.
How can you solve a multi-step inequality?
Answer:
a) Clear parenthesis i.e., Brackets on both sides of the inequality and collect like terms
b) Addor subtract terms so the variable is on one side and the constant is on another side of the inequality sign
Question 3.
Write two different multi-step inequalities whose solutions are represented by the graph.
Answer:
The marking started from -1 but by excluding -1 and continued till the left end of the graph.
The inequality represented by the graph is given as,
x < -1
2.4 Lesson
Monitoring Progress
Solve the inequality. Graph the solution.
Question 1.
4b – 1 < 7
Answer:
4b – 1 < 7
So,
4b < 7 + 1
4b < 8
b < 8 / 4
b < 2

Question 2.
8 – 9c ≥ -28
Answer:
8 – 9c ≥ -28
-9c ≥ -28 – 8
-9c ≥ -36
9c ≥ 36
c ≥ 36 / 9
c ≥ 4

Question 3.
\(\frac{n}{-2}\) + 11 > 12
Answer:
\(\frac{n}{-2}\) + 11 > 12
\(\frac{n}{-2}\) > 12 – 11
\(\frac{n}{-2}\) > 1
n > 1 (-2)
n > -2

Question 4.
6 ≥ 5 – \(\frac{v}{3}\)
Answer:
6 ≥ 5 – \(\frac{v}{3}\)
6 – 5 ≥ – \(\frac{v}{3}\)
-1 ≥ \(\frac{v}{3}\)
-3 ≥ v
v ≤ -3

Solve the inequality.
Question 5.
5x – 12 ≤ 3x – 4
Answer:
5x – 12 ≤ 3x – 4
5x – 3x ≤ 12 – 4
2x ≤ 8
x ≤ 8 / 2
x ≤ 4
Question 6.
2(k – 5) < 2k + 5
Answer:
2 ( k – 5 ) < 2k + 5
2 ( k ) – 2 ( 5 ) < 2k + 5
2k – 10 < 2k + 5
2k – 2k < 5 + 10
-10 < 5
Question 7.
-4(3n – 1) > -12n + 5.2
Answer:
-4 ( 3n – 1 ) > -12n + 5.2
-4 ( 3n ) – 4 ( -1 ) > -12n + 5.2
-12n + 4 > -12n + 5.2
-12n + 12n + 4 > 5.2
4 > 5.2
Question 8.
3(2a – 1) ≥ 10a – 11
Answer:
3 ( 2a – 1 ) ≥ 10a – 11
3 ( 2a ) – 3 ( 1 ) ≥ 10a – 11
6a – 3 ≥ 10a – 11
6a – 10a ≥ -11 + 3
-4a ≥ -8
4a ≥ 8
a ≥ 8 / 4
a ≥ 2
Question 9.
WHAT IF?
You need a mean score of at least 85 points to advance to the next round. What scores in the fifth game will allow you to advance?
Answer:
You need a mean score of at least 85 points to advance to the next round.
(95 + 91 + 77 + 89 + x)/5 ≥ 85
(352 + x)/5 ≥ 85
85 × 5 = 425
352 + x ≥ 425
x = 425 – 352
x = 73
Solving Multi-step Inequalities 2.4 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Compare solving multi-step inequalities and solving multi-step equations.
Answer:

Question 2.
WRITING
Without solving, how can you tell that the inequality 4x + 8 ≤ 4x – 3 has no solution?
Answer:
4x + 8 ≤ 4x – 3
4x – 4x ≤ -3 – 8
0 + 8 ≤ -3
8 ≤ -3
In Exercises 3–6, match the inequality with its graph.
Question 3.
7b – 4 ≤ 10
Answer:

Question 4.
4p + 4 ≥ 12
Answer:
4p + 4 ≥ 12
4p ≥ 12 – 4
4p ≥ 8
p ≥ 8 / 4
p ≥ 2
Question 5.
-6g + 2 ≥ 20
Answer:

Question 6.
3(2 – f) ≤ 15
Answer:
3 (2 – f) ≤ 15
3 (2) – 3 (f) ≤ 15
6 – 3f ≤ 15
-3f ≤ 15 – 6
-3f ≤ 9
f ≤ -9 / 3
f ≤ -3
In Exercises 7–16, solve the inequality. Graph the solution.
Question 7.
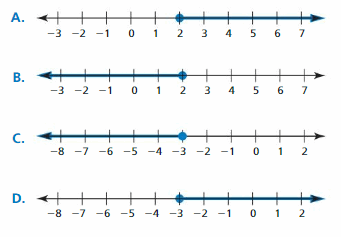
2x – 3 > 7
Answer:
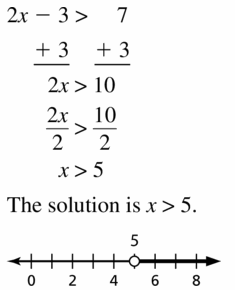
Question 8.
5y + 9 ≤ 4
Answer:
5y + 9 ≤ 4
5y ≤ 4 -9
5y ≤ -5
y ≤ -5 / 5
y ≤ -1

Question 9.
-9 ≤ 7 – 8v
Answer:
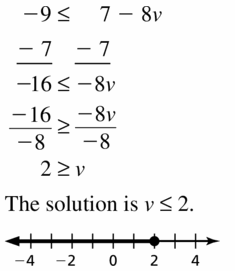
Question 10.
2 > -3t – 10
Answer:
2 > -3t – 10
2 + 10 > -3t
12 > -3t
-12 / 3 > t
-4 > t
t < -4

Question 11.
\(\frac{w}{2}\) + 4 > 5
Answer:
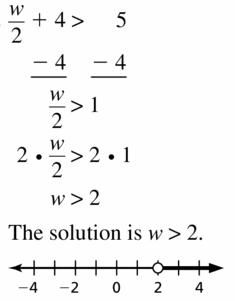
Question 12.
1 + \(\frac{m}{3}\) ≤ 6
Answer:
1 + \(\frac{m}{3}\) ≤ 6
\(\frac{m}{3}\) ≤ 6 – 1
\(\frac{m}{3}\) ≤ 5
m ≤ 5 (3)
m ≤ 15

Question 13.
\(\frac{p}{-8}\) + 9 > 13
Answer:
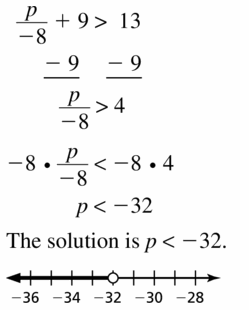
Question 14.
3 + \(\frac{r}{-4}\) ≤ 6
Answer:
3 + \(\frac{r}{-4}\) ≤ 6
\(\frac{r}{-4}\) ≤ 6 – 3
\(\frac{r}{-4}\) ≤ 3
r ≤ 3 (-4)
r ≤ -12

Question 15.
6 ≥ -6(a + 2)
Answer:
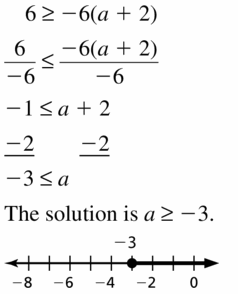
Question 16.
18 ≤ 3(b – 4)
Answer:
18 ≤ 3 (b – 4)
18 ≤ 3 (b) – 3 (4)
18 ≤ 3b – 12
18 + 12 ≤ 3b
30 ≤ 3b
30 / 3 ≤ b
10 ≤ b
b ≥ 10

In Exercises 17–28, solve the inequality.
Question 17.
4 – 2m > 7 – 3m
Answer:
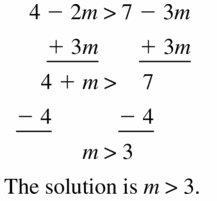
Question 18.
8n+ 2 ≤ 8n – 9
Answer:
8n + 2 ≤ 8n – 9
8n – 8n + 2 ≤ -9
2 ≤ 9
Question 19.
-2d – 2 < 3d + 8
Answer:
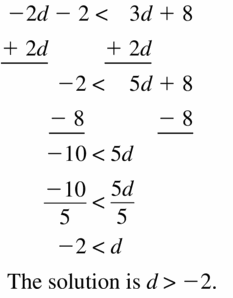
Question 20.
8 + 10f > 14 – 2f
Answer:
8 + 10f > 14 – 2f
10f + 2f > 14 – 8
12f > 6
f > 6 / 12
f > \(\frac{1}{2}\)
Question 21.
8g – 5g – 4 ≤ -3 + 3g
Answer:
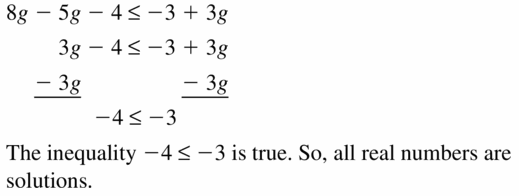
Question 22.
3w – 5 > 2w + w – 7
Answer:
3w – 5 > 2w + w – 7
3w – 5 > 3w – 7
3w – 5 – 3w > -7
-5 > -7
5 > 7
Question 23.
6(ℓ + 3) < 3(2ℓ + 6)
Answer:
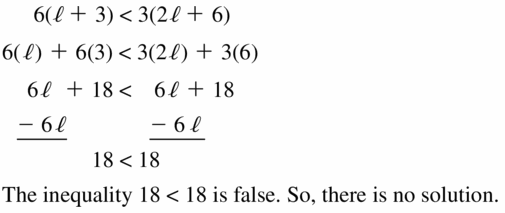
Question 24.
2(5c – 7) ≥ 10(c – 3)
Answer:
2 (5c – 7) ≥ 10 (c – 3)
2 (5c) – 2 (7) ≥ 10 (c) – 10 (3)
10c – 14 ≥ 10c – 30
10c – 10c – 14 ≥ -30
-14 ≥ -30
14 ≥ 30
Question 25.
4 (\(\frac{1}{2}\)t – 2 )> 2(t – 3)
Answer:
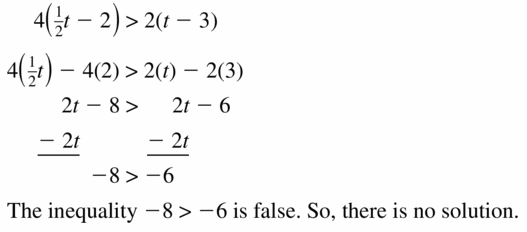
Question 26.
15 (\(\frac{1}{3}\)b + 3 ) ≤ 6(b + 9)
Answer:
15 ( (\(\frac{1}{3}\)b + 3 ) ) ≤ 6 (b + 9)
15 ( (\(\frac{1}{3}\)b ) ) + 15 (3) ≤ 6 (b) + 6 (9)
5b + 45 ≤ 6b + 54
5b – 6b ≤ 54 – 45
-b ≤ 9
b ≤ -9
Question 27.
9j – 6 + 6j ≥ 3(5j – 2)
Answer:
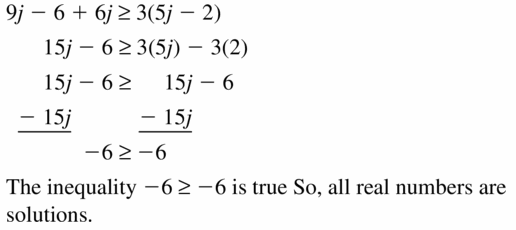
Question 28.
6h – 6 + 2h < 2(4h – 3)
Answer:
6h – 6 + 2h < 2 (4h – 3)
8h – 6 < 2 (4h) – 2 (3)
8h – 6 < 8h – 6
8h – 8h < -6 + 6
0 < 0
ERROR ANALYSIS
In Exercises 29 and 30, describe and correct the error in solving the inequality.
Question 29.

Answer:

Question 30.
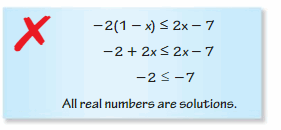
Answer:
-2 (1 – x) ≤ 2x – 7
-2 (1) + 2 (x) ≤ 2x – 7
-2 + 2x ≤ 2x – 7
-2 + 2x – 2x ≤ -7
-2 ≤ -7
2 ≤ 7
Question 31.
MODELING WITH MATHEMATICS
Write and solve an inequality that represents how many $20 bills you can withdraw from the account without going below the minimum balance.
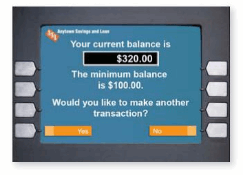
Answer:

Question 32.
MODELING WITH MATHEMATICS
A woodworker wants to earn at least $25 an hour making and selling cabinets. He pays $125 for materials. Write and solve an inequality that represents how many hours the woodworker can spend building the cabinet.

Answer:
A woodworker wants to earn at least $25 an hour making and selling cabinets. He pays $125 for materials.
Let x be the number of hours taken by the woodworker to build the cabinet
The inequality is
25 (x) ≥ 125
x ≥ 125 / 25
x ≥ 5
Question 33.
MATHEMATICAL CONNECTIONS
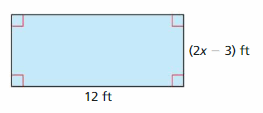
The area of the rectangle is greater than 60 square feet. Write and solve an inequality to find the possible values of x.
Answer:

Question 34.
MAKING AN ARGUMENT
Forest Park Campgrounds charges a $100 membership fee plus $35 per night. Woodland Campgrounds charges a $20 membership fee plus $55 per night. Your friend says that if you plan to camp for four or more nights, then you should choose Woodland Campgrounds. Is your friend correct? Explain.
Answer:
Given,
Forest Park Campgrounds charges a $100 membership fee plus $35 per night. Woodland Campgrounds charges a $20 membership fee plus $55 per night.
Let x be the number of nights you spend
The charge of the Forest Park Campgrounds for x nights = 100 + 35x
The charge of the Woodland Campgrounds = 20 + 55x
It is given that for four or more nights i.e., x ≥ 4, you will choose Woodland Campgrounds
20 + 55x ≥ 100 + 35x
55x – 35x ≥ 100 – 20
20x ≥ 80
x ≥ 80 / 20
x ≥ 4
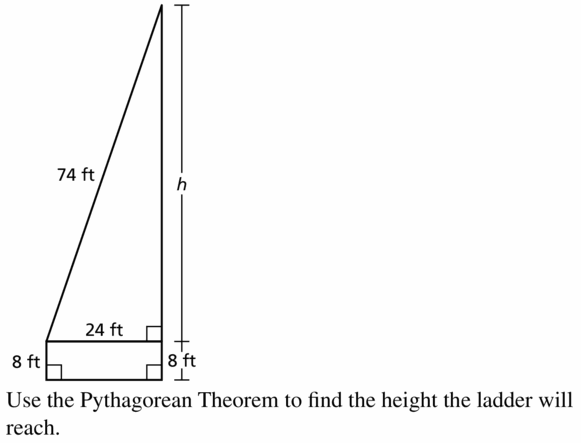
Question 35.
PROBLEM-SOLVING
The height of one story of a building is about 10 feet. The bottom of the ladder on the truck must be at least 24 feet away from the building. How many stories can the ladder reach? Justify your answer.

Answer:

Question 36.
HOW DO YOU SEE IT?
The graph shows your budget and the total cost of x gallons of gasoline and a car wash. You want to determine the possible amounts (in gallons) of gasoline you can buy within your budget.
a. What is your budget?
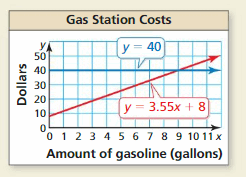
Answer:
We can observe that x-axis represents the amount of gasoline ( gallons ) and the y-axis represents the budget
The line is represented parallel to the x-axis i.e., the Budget
y = 40
So, the budget is $40
b. How much does a gallon of gasoline cost? How much does a car wash cost?
Answer:
It is given that the graph shows your budget and the total cost of x gallons of gasoline and a car wash.
The x-axis represents the amount of gasoline
The equation represented by the x-axis is
y = 3.55x + 8
The coefficient of x represents the cost of x gallons of gasoline and the constant term represents the cost of a car wash
The cost of a gallon of gasoline is $3.55
The cost of a car wash is $8
c. Write an inequality that represents the possible amounts of gasoline you can buy.
Answer:
The x-axis represents the amount of gasoline you can buy
y = 3.55x + 8
The budget will be less than or equal to $40
3.55x + 8 ≤ 40
3.55x ≤ 40 – 8
3.55x ≤ 32
x ≤ 32 / 3.55
x ≤ 9 [ Approx. ]
d. Use the graph to estimate the solution of your inequality in part (c).
Answer:
The required inequality is:
3.55x + 8 ≤ 40
We can see that the x-axis and y-axis intersected at one particular point.
This particular point is the estimated solution to the inequality
The particular point = (x , y ) = ( 9 , 40 )
Hence, the estimated solution to your inequality in part (c) is ( 9, 40 )
Question 37.
PROBLEM-SOLVING
For what r values of r will the area of the shaded region be greater than or equal to 9(π – 2)?
Answer:

Question 38.
THOUGHT-PROVOKING
A runner’s times (in minutes) in the four races he has completed are 25.5, 24.3, 24.8, and 23.5. The runner plans to run at least one more race and wants to have an average time of less than 24 minutes. Write and solve an inequality to show how the runner can achieve his goal.
Answer:
A runner’s times (in minutes) in the four races he has completed are 25.5, 24.3, 24.8, and 23.5.
The runner plans to run at least one more race and wants to have an average time of less than 24 minutes.
Let x be the time in the fifth race [ Since it is given that the runner plans to run at least one more race ]
Average = \(\frac{The sum of all the items}{The number of items}\)
Average = \(\frac{25.5 + 24.3 + 24.8 + 23.5 + x}{5}\)
Average = \(\frac{98.1 + x}{5}\)
It is given that the average time will be less than 24 minutes
\(\frac{98.1 + x}{5}\) < 24
98.1 + x < 24 (5)
98.1 + x < 120
x < 120 – 98.1
x < 21.9 minutes
So, the inequality that shows the runner can achieve his goal is x < 21.9 minutes
REASONING
In Exercises 39 and 40, find the value of a for which the solution of the inequality is all real numbers.
Question 39.
a(x + 3) < 5x + 15 – x
Answer:
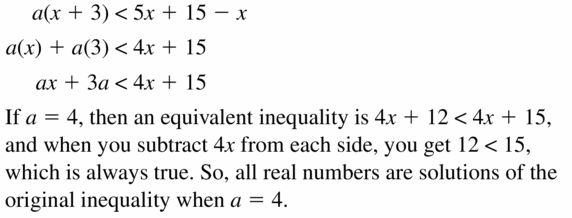
Question 40.
3x + 8 + 2ax ≥ 3ax – 4a
Answer:
3x + 8 + 2ax ≥ 3ax – 4a
3x + 2ax – 3ax ≥ -4a – 8
3x – ax ≥ -4a – 8
x = 0
To make x = 0,
We can observe from the inequality that ‘a’ must be equal to 3
So, the value of a is: 3
Maintaining Mathematical Proficiency
Write the sentence as an inequality. (Section 2.1)
Question 41.
Six times a number y is less than or equal to 10.
Answer:
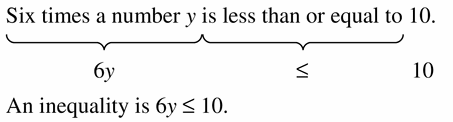
Question 42.
A number p plus 7 is greater than 24.
Answer:
A number p plus 7 is greater than 24
The representation of the worded form in the form of inequality is p + 7 > 24
Question 43.
The quotient of a number r and 7 is no more than 18.
Answer:
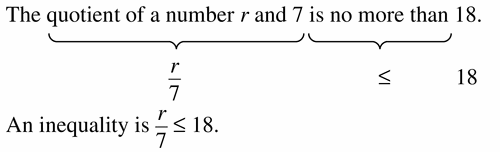
Solving Linear Inequalities Study Skills: Analyzing Your Errors
2.1–2.4 What Did You Learn?
Core Vocabulary

Core Concepts
Section 2.1
Representing Linear Inequalities, p. 57
Section 2.2
![]()
Section 2.3
Multiplication and Division Properties of Inequality (c > 0), p. 68
Multiplication and Division Properties of Inequality (c < 0), p. 69
Section 2.4
Solving Multi-Step Inequalities, p. 74
Special Solutions of Linear Inequalities, p. 75
Mathematical Practices
Question 1.
Explain the meaning of the inequality symbol in your answer to Exercise 47 on page 59. How did you know which symbol to use?
Answer:
In Exercise 47 on page 59,
The inequality symbol we used is ≤
The meaning of ≤ is ” Less than or equal to ”
In Exercise 47,
It is given that the Xianren bridge arch is the longest natural arch with a length of 400 feet i.e., there is no arch longer than the Xianren bridge arch and the remaining natural arches are shorter than the Xianren arch
The lengths of all the arches including the Xianren arch will be represented by the inequality symbol “≤”
Question 2.
In Exercise 30 on page 66, why is it important to check the reasonableness of your answer in part (a) before answering part (b)?
Answer:
In part (a), it is given that you have to beat your competitor with your score.
Your score must be greater than your competitor
Then only you can solve part (b).
Question 3.
Explain how considering the units involved in Exercise 29 on page 71 helped you answer the question.
Answer:
In Exercise 29 on page 71,
The mat that is given is in the form of a square since its length and width both are the same
Area of the square = Side²
Let the cost per square foot be x
The inequality formed will be like
( Area of the square ) ⋅ x ≤ $700
Study Skills
Analyzing Your Errors
Application Errors
What Happens: You can do numerical problems, but you struggle with problems that have context.
How to Avoid This Error: Do not just mimic the steps of solving an application problem. Explain out loud what the question is asking and why you are doing each step. After solving the problem, ask yourself, “Does my solution make sense?”

Solving Linear Inequalities Maintaining 2.1 – 2.4 Quiz
Write the sentence as an inequality. (Section 2.1)
Question 1.
A number z minus 6 is greater than or equal to 11.
Answer:
A number z minus 6 is greater than or equal to 11
The representation of the worded form in the form of inequality is z – 6 ≥ 11
Question 2.
Twelve is no more than the sum of -1.5 times a number w and 4.
Answer:
Twelve is no more than the sum of -1.5 times a number w and 4
The representation of the worded form in the form of inequality is 12 ≤ -1.5w + 4
Write an inequality that represents the graph.(Section 2.1)
Question 3.

Answer:
We can observe that the marked line started from 0 excludes 0 and continued till the left end of the number line
The inequality that represents the given graph is
x < 0
Question 4.

Answer:
The marked line started from 8 which includes 8 and continued till the right end of the number line.
The inequality that represents the given graph is:
x ≥ 8
Solve the inequality. Graph the solution. (Section 2.2 and Section 2.3)
Question 5.
9 + q ≤ 15
Answer:
Given,
9 + q ≤ 15
q ≤ 15 – 9
q ≤ 6

Question 6.
z – (-7) < 5
Answer:
Given,
z – (-7) < 5
z + 7 < 5
z < 5 – 7
z < -2

Question 7.
-3 < y – 4
Answer:
-3 < y – 4
So,
-3 + 4 < y
1 < y
y > 1

Question 8.
3p ≥ 18
Answer:
3p ≥ 18
p ≥ 18 / 3
p ≥ 6

Question 9.
6 > \(\frac{w}{-2}\)
Answer:
Given,
6 > \(\frac{w}{-2}\)
6 (-2) > w
-12 > w
w < -12

Question 10.
-20x > 5
Answer:
-20x > 5
x > -5 / 20
x > – \(\frac{1}{4}\)
![]()
Solve the inequality. (Section 2.4)
Question 11.
3y – 7 ≥ 17
Answer:
3y – 7 ≥ 17
3y ≥ 17 + 7
3y ≥ 24
y ≥ 24 / 3
y ≥ 8
Question 12.
8(3g – 2) ≤ 12(2g + 1)
Answer:
8 (3g – 2) ≤ 12 (2g + 1)
8 (3g) – 8 (2) ≤ 12 (2g) + 12 (1)
24g – 16 ≤ 24g + 12
24g – 24g – 16 ≤ 12
-16 ≤ 12
Question 13.
6(2x – 1) ≥ 3(4x + 1)
Answer:
Given,
6 (2x – 1)≥ 3 (4x + 1)
6 (2x) – 6 (1) ≥ 3 (4x) + 3 (1)
12x – 6 ≤ 12x + 3
12x – 6 – 12x ≤ 3
-6 ≤ 3
Question 14.
Three requirements for a lifeguard training course are shown. (Section 2.1)
a. Write and graph three inequalities that represent the requirements.
b. You can swim 250 feet, tread water for 6 minutes, and swim 35 feet underwater without taking a breath. Do you satisfy the requirements of the course? Explain.

Answer:
a.
The given requirements are:
1. Swim at least 100 yards
2. Tread water for at least 5 minutes
3. Swim 10 yards or more underwater without taking a breath
Now,
1. The inequality that represents the first requirement is:
x ≥ 100 yards
2. The inequality that represents the second requirement is:
x ≥ 5 minutes
3. The inequality that represents the third requirement is:
x ≥ 10 yards
b.
From part (a),
The inequalities for the three requirements are:
x ≥ 100 yards
x ≥ 5 minutes
x ≥ 10 yards
Question 15.
The maximum volume of an American white pelican’s bill is about 700 cubic inches. A pelican scoops up 100 cubic inches of water. Write and solve an inequality that represents the additional volumes the pelican’s bill can contain. (Section 2.2)
Answer:
Given,
The maximum volume of an American white pelican’s bill is about 700 cubic inches. A pelican scoops up 100 cubic inches of water.
Let x be the additional volumes the pelican’s bill can contain
The maximum volume is 700 cubic inches and a pelican’s bill scoops up 100 cubic inches of water
The inequality that represents the additional volumes of the pelican’s bill can contain is
x + 100 ≤ 700
x ≤ 700 – 100
x ≤ 600
Question 16.
You save $15 per week to purchase one of the bikes shown. (Section 2.3and Section 2.4)
a. Write and solve an inequality to find the numbers of weeks you need to save to purchase a bike.
b. Your parents give you $65 to help you buy the new bike. How does this affect your answer in part (a)? Use an inequality to justify your answer.

Answer:
a.
You save $15 per week to purchase one of the bikes
It is given that the starting price of the bike is $120
Let x be the number of weeks
The inequality that represents the number of weeks you need to save to purchase a bike is
15 ⋅ x ≥ 120
15x ≥ 120
x ≥ 120 / 15
x ≥ 8
The number of weeks you need to save to purchase a bike is 8 weeks
b.
Your parents give you $65 to help you buy the new bike.
The starting price of the bike is $120
The remaining amount that needs to purchase a bike = 120 – 65 = $55
Lesson 2.5 Solving Compound Inequalities
Essential Question
How can you use inequalities to describe intervals on the real number line?
EXPLORATION 1
Describing Intervals on the Real Number
Work with a partner.
In parts (a)–(d), use two inequalities to describe the interval.
e. Do you use “and” or “or” to connect the two inequalities in parts (a)–(d)? Explain.
Answer:
(a) – (d):
The given graphs are:

a.
The marked line starting from -3 excluding -3 and continued till -6 including -6
The inequality that represents the given interval is
x ≥ -6 and x < -3
The compound inequality that represents the given interval is
-6 ≤ x < -3
b.
The marked line starting from -5 excluding -5 and continued till 4 including 4
The inequality that represents the given interval is
x > -5 and x < 4
The compound inequality that represents the given interval is
-5 < x < 4
c.
The marked line starting from -4 including -4 and continued till 5 including 5
The inequality that represents the given interval is
x ≥ -4 and x ≤ 5
The compound inequality that represents the given interval is
-4 ≤ x ≤ 5
d.
The marked line starting from -3 excluding -3 and continued till 6 including 6
The inequality that represents the given interval is
x > -3 and x < 6
The compound inequality that represents the given interval is
-3 < x < 6
e.
We use “and” to connect the two inequalities in parts (a) – (d)
From (a) – (d),
For Half-open interval,
We use ≥ and <
For closed interval,
We use ≥ and ≤
For open interval,
We use > and <
EXPLORATION 2
Describing Two Infinite Intervals
Work with a partner. In parts (a)–(d), use two inequalities to describe the interval.
e. Do you use “and” or “or” to connect the two inequalities in parts (a)–(d)? Explain.
Answer:
The given graphs are:

(a) – (d):
a.
The first marked line starting from -6 including -6 and continued till the end of the left side of the graph
The second marked line starting from 3 excluding 3 and continued till the end of the right side of the graph
The inequality that represents the given intervals are
x ≤ -6 and x > 3
The compound inequality that represents the given interval is
-6 ≤ x > 3
b.
The first marked line starting from -5 excluding -5 and continued till the end of the left side of the graph
The second marked line starting from 4 including 4 and continued till the end of the right side of the graph
The inequality that represents the given intervals are
x < -5 and x ≥ 4
The compound inequality that represents the given interval is
-5 < x ≥ 4
c.
The first marked line starting from -4 including -4 and continued till the end of the left side of the graph
The second marked line starting from 5 including 5 and continued till the end of the right side of the graph
The inequality that represents the given intervals are
x ≤ -4 and x ≥ 5
The compound inequality that represents the given interval is
-4 ≤ x ≥ 5
d.
The first marked line starting from -3 excluding -3 and continued till the end of the left side of the graph
The second marked line starting from 6 excluding 6 and continued till the end of the right side of the graph
The inequality that represents the given intervals are
x < -3 and x > 6
The compound inequality that represents the given interval is
-3 < x > 6
e.
From (a) – (d),
For Half-open interval,
We use ≥ and <
For closed interval,
We use ≥ and ≤
For open interval,
We use > and <
Communicate Your Answer
Question 3.
How can you use inequalities to describe intervals on the real number line?
Answer:
An inequality that includes the boundary point indicated by the “or equal” part of the symbols ≤ and ≥ with a closed dot on the number line. The symbol (∞) indicates the interval is unbounded to the right. Express ordering relationships using the symbol < for “less than” and > for “greater than.”
2.5 Lesson
Monitoring Progress
Write the sentence as an inequality. Graph the inequality.
Question 1.
A number d is more than 0 and less than 10.
Answer:
A number d is more than 0 and less than 10
The representation of the given worded form in the form of inequality is
d > 0 and d < 10
The representation of the inequalities in the form of compound inequality is
0 < d < 10

Question 2.
A number a is fewer than -6 or no less than -3.
Answer:
A number a is fewer than -6 or no less than -3
The representation of the given worded form in the form of inequality is
a < -6 or a > -3

Solve the inequality. Graph the solution.
Question 3.
5 ≤ m + 4 < 10
Answer:
5 ≤ m + 4 < 10
Subtract by 4 on both sides
5 – 4 ≤ m + 4 – 4 < 10 – 4
1 ≤ m < 6

Question 4.
-3 < 2k – 5 < 7
Answer:
-3 < 2k – 5 < 7
-3 + 5 < 2k – 5 + 5 < 7 + 5
2 < 2k < 12
1 < k < 6

Question 5.
4c + 3 ≤ -5 or c – 8 > -1
Answer:
4c + 3 ≤ -5 or c – 8 > -1
4c ≤ -5 – 3 or c > -1 + 8
4c ≤ -8 or c > 7
c ≤ -8 / 4 or c > 7
c ≤ -2 or c > 7

Question 6.
2p + 1 < -7 or 3 – 2p ≤ -1
Answer:
2p + 1 < -7 or 3 – 2p ≤ -1
2p < -7 – 1 or -2p ≤ -1 – 3
2p < -8 or -2p ≤ -4
p < -8 / 2 or p ≤ -4 / (-2)
p < -4 or p ≤ 2

Question 7.
Write and solve a compound inequality that represents the temperature rating (in degrees Fahrenheit) of the winter boots.

Answer:
The range of the temperature rating ( In °C ) of the winter boots is: -40°C to 15°C
°F = ( °C × \(\frac{9}{5}\) ) + 32
To convert -40°C into °F,
°F = ( -40°C × \(\frac{9}{5}\) ) + 32
°F = -72 + 32
°F = – 40°F
To convert 15°C into °F,
°F = ( 15 × \(\frac{9}{5}\) ) + 32
°F = 27 + 32
°F = 59°F
Let t be the temperature in °F
The representation of the temperature ranges in the form of inequalities is t > -40°F and t < 59°F
The representation of the temperature ranges in the form of compound inequality is -40°F < t < 59°F
Solving Compound Inequalities 2.5 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Compare the graph of -6 ≤ x ≤ -4 with the graph of x ≤ -6 or x ≥ -4.
Answer:

Question 2.
WHICH ONE do DOESN’T BELONG?
Which compound inequality does not belong with the other three? Explain your reasoning.
![]()
Answer:
a. a > 4 or a < -3

b. a < -2 or a > 8

c.
a > 7 or a < -5

d.
a < 6 or a > -9

C does not belong with the other three inequalities
In Exercises 3–6, write a compound inequality that is represented by the graph.
Question 3.
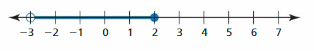
Answer:
![]()
Question 4.
![]()
Answer:
The marked line started from 7 excluding 7 and continued till 14 excluding 14
The representation of the inequalities from the given graph is
x > 7 and x < 14
The representation of the inequalities in the form of compound inequality is
7 < x < 14
Question 5.
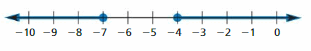
Answer:
![]()
Question 6.
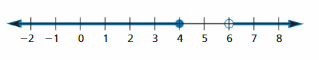
Answer:
The first marked line started from 4 including 4 and continued till the end of the left end of the graph.
The second marked line started from 6 excluding 6 and continued till the end of the right end of the graph.
The representation of the given graph in the form of inequality is x ≤ 4 or x > 6
In Exercises 7–10, write the sentence as an inequality. Graph the inequality.
Question 7.
A number p is less than 6 and greater than 2.
Answer:
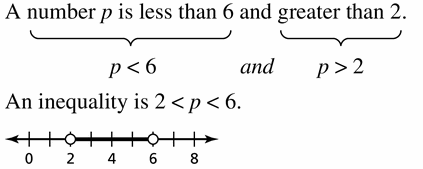
Question 8.
A number n is less than or equal to -7 or greater than 12.
Answer:
A number n is less than or equal to -7 or greater than 12
The representation of the given worded form in the form of inequality is
n ≤ -7 or n > 12

Question 9.
A number m is more than -7\(\frac{2}{3}\) or at most -10.
Answer:
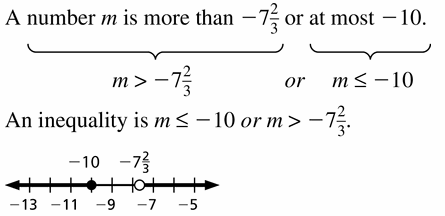
Question 10.
A number r is no less than -1.5 and fewer than 9.5.
Answer:
A number r is no less than -1.5 and fewer than 9.5
The representation of the given worded form in the form of inequality is
r > -1.5 and r < 9.5
The representation of the given worded form in the form of compound inequality is
-1.5 < r < 9.5

Question 11.
MODELING WITH MATHEMATICS
Slitsnails are large mollusks that live in deep waters. They have been found in the range of elevations shown. Write and graph a compound inequality that represents this range.

Answer:

Question 12.
MODELING WITH MATHEMATICS
The life zones on Mount Rainier, a mountain in Washington, can be approximately classified by elevation, as follows.
Low-elevation forest: above 1700 feet to 2500 feet mid-elevation forest: above 2500 feet to 4000 feet Subalpine: above 4000 feet to 6500 feet
Alpine: above 6500 feet to the summit

Write a compound inequality that represents the elevation range for each type of plant life.
a. trees in the low-elevation forest zone
b. flowers in the subalpine and alpine zones
Answer:
a.
The inequality that represents the elevation range of trees in the low-elevation forest zone is
x > 1700 feet and x < 2500 feet
The representation of the elevation range of trees in the low-elevation forest zone in the form of compound inequality is
1700 feet < x < 2500 feet
b.
The inequalities that represent the elevation range of trees in the subalpine and alpine zones is
Subalpine zone: x > 4000 feet and x < 6500 feet
Alpine zone: x > 6500 feet
The representation of the elevation range of trees in the Subalpine zone and Alpine zone in the form of compound inequality is:
Subalpine zone: 4000 feet < x < 6500 feet
Alpine zone: x > 6500 feet
In Exercises 13–20, solve the inequality. Graph the solution.
Question 13.
6 < x + 5 ≤ 11
Answer:
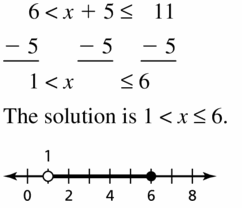
Question 14.
24 > -3r ≥ -9
Answer:
24 > -3r ≥ -9
( 24 / 3 ) > ( -3r / 3 ) ≥ ( -9 / 3 )
8 > -r ≥ -3
-8 < r ≤ 3

Question 15.
v + 8 < 3 or -8v < -40
Answer:
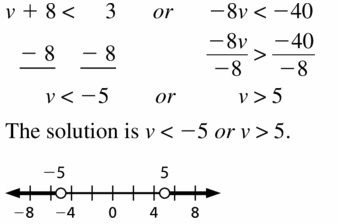
Question 16.
-14 > w + 3 or 3w ≥ -27
Answer:
Given,
-14 > w + 3 or 3w ≥ -27
-14 – 3 > w or w ≥ -27 / 3
-17 > w or w ≥ -9
w < -17 or w ≥ -9
![]()
Question 17.
2r + 3 < 7 or -r + 9 ≤ 2
Answer:
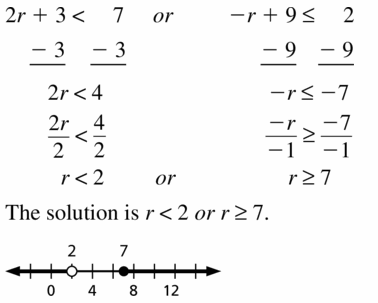
Question 18.
-6 < 3n + 9 < 21
Answer:
-6 < 3n + 9 < 21
-6 – 9 < 3n + 9 – 9 < 21 – 9
-15 < 3n < 12
( -15 / 3 ) < ( 3n / 3 ) < ( 12 / 3 )
-5 < n < 4

Question 19.
-12 < \(\frac{1}{2}\)(4x + 16) < 18
Answer:
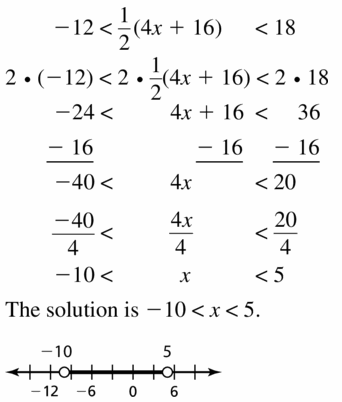
Question 20.
35 < 7(2 – b) or \(\frac{1}{3}\)(15b – 12) ≥ 21
Answer:
35 < 7 (2 – b) or \(\frac{1}{3}\) ( 15b – 12 ) ≥ 21
35 < 7 (2) – 7 (b) or 15b – 12 ≥ 21 (3)
35 < 14 – 7b or 15b – 12 ≥ 63
7b < 14 – 35 or 15b ≥ 63 + 12
7b < -21 or 15b ≥ 75
b < -21 / 7 or b ≥ 75 / 15
b < -3 or b ≥ 5

ERROR ANALYSIS
In Exercises 21 and 22, describe and correct the error in solving the inequality or graphing the solution.
Question 21.
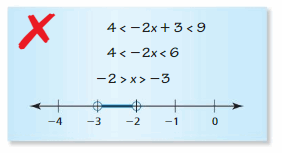
Answer:

Question 22.
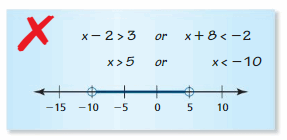
Answer:
x – 2 > 3 or x + 8 < -2
x > 3 + 2 or x < -2 – 8
x > 5 or x < -10
![]()
Question 23.
MODELING WITH MATHEMATICS
Write and solve a compound inequality that represents the possible temperatures (in degrees Fahrenheit) of the interior of the iceberg.

Answer:
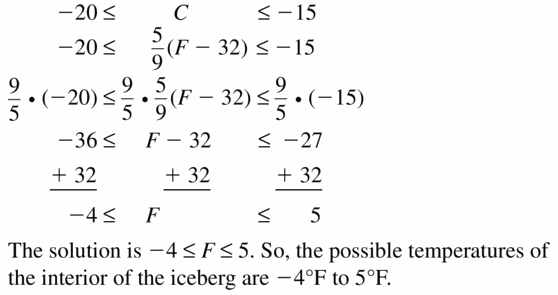
Question 24.
PROBLEM-SOLVING
A ski shop sells skis with lengths ranging from 150 centimeters to 220 centimeters. The shop says the length of the skis should be about 1.16 times a skier’s height (in centimeters). Write and solve a compound inequality that represents the heights of skiers the shop does not provide skis for.
Answer:
Ski shop sells skis with lengths ranging from 150 centimeters to 220 centimeters.
The shop says the length of the skis should be about 1.16 times a skier’s height (in centimeters).
Let x be the possible length of the skis
Let h be the possible height of the skiers for whom the shop does not provide skis
The inequality that represents the lengths of the skis is
x < 150 centimeters or x > 220 centimeters
The compound inequality that represents the length of the skis is
150 centimeters > x > 220 centimeters
x = 1.16h
150 centimeters > 1.16h > 220 centimeters
(150 / 1.16) centimeters > h > (220 / 1.16) centimeters
129.3 centimeters > h > 189.7 centimeters
In Exercises 25–30, solve the inequality. Graph the solution, if possible.
Question 25.
22 < -3c + 4 < 14
Answer:
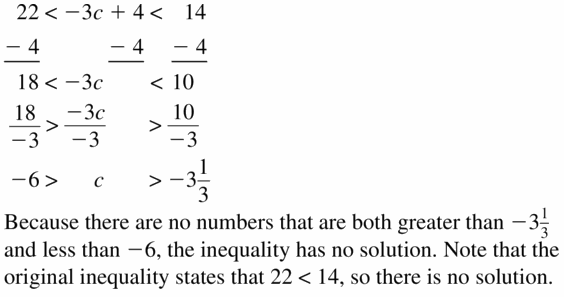
Question 26.
2m – 1 ≥ 5 or 5m > -25
Answer:
2m – 1≥ 5 or 5m > -25
2m ≥ 5 + 1 or m > -25 / 5
2m ≥ 6 or m > -5
m ≥ 6 / 2 or m > -5
m ≥ 3 or m > -5
We can conclude that the solutions to the given inequality are
m ≥ 3 or m > -5
The compound inequality of the solutions of the given inequality is
m > -5

Question 27.
-y + 3 ≤ 8 and y + 2 > 9
Answer:
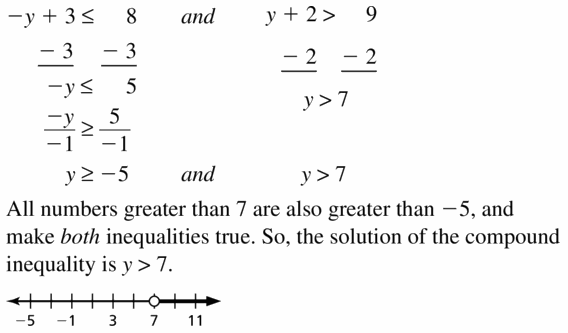
Question 28.
x – 8 ≤ 4 or 2x + 3 > 9
Answer:
x – 8 ≤ 4 or 2x + 3 > 9
x ≤ 4 + 8 or 2x > 9 – 3
x ≤ 12 or 2x > 6
x ≤ 12 or x > 6 / 2
x ≤ 12 or x > 3
We can conclude that the solutions to the given inequality are
x ≤ 12 or x > 3
The compound inequality of the solutions of the given inequality is
3 < x ≤ 12

Question 29.
2n + 19 ≤ 10 + n or -3n + 3 < -2n + 33
Answer:
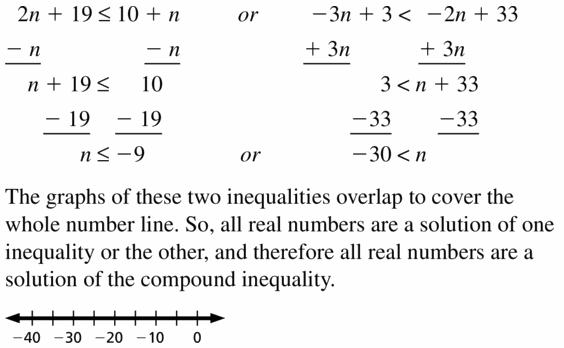
Question 30.
3x – 18 < 4x – 23 and x – 16 < -22
Answer:
3x – 18 < 4x – 23 and x – 16 < -22
3x – 4x < -23 + 18 and x < -22 + 16
-x < -5 and x < – 6
x < 5 and x < -6
We can conclude that the solutions to the given inequality are
x < 5 and x < -6
The compound inequality that represents the solutions of the given inequality is
x < 5

Question 31.
REASONING
Fill in the compound inequality ![]() and 5(x + 2) ≥ 2(x + 8) with <, ≤, >, or ≥ so that the solution is only one value.
and 5(x + 2) ≥ 2(x + 8) with <, ≤, >, or ≥ so that the solution is only one value.
Answer:
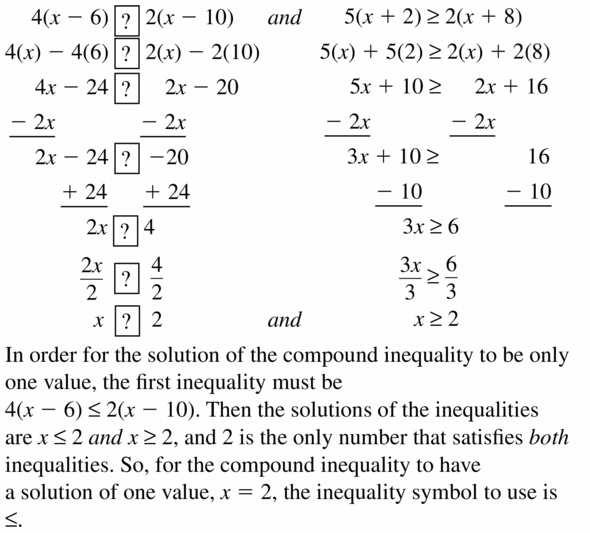
Question 32.
THOUGHT-PROVOKING
Write a real-life story that can be modeled by the graph.
Answer:
Suppose we have 100 children in a school. Out of the 100 children, there are 60 boys and the rest are girls.
The attendance of all the boys in a particular month is 50% and all of the girls is 70%. Mark the percentage attendance that is between the attendance of all the boys and girls?

Question 33.
MAKING AN ARGUMENT
The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Use the triangle shown to write and solve three inequalities. Your friend claims the value of x can be 1. Is your friend correct? Explain.
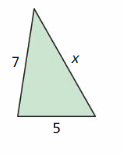
Answer:
Question 34.
HOW DO YOU SEE IT?
The graph shows the annual profits of a company from 2006 to 2013.
a. Write a compound inequality that represents the annual profits from 2006 to 2013.
Answer:
We can observe that the annual profits from 2006 to 2013
The minimum value in the graph is: $65 million
The highest value in the graph is: $100 million
Let x be the annual profit
The inequalities that represent the annual profits from 2006 to 2013 are
x ≥ $65 million and x ≤ $100 million
The compound inequality that represents the annual profits from 2006 to 2013 is
$65 million ≤ x ≤ $100 million
b. You can use the formula P = R – C to find the profit P, where R is the revenue and C is the cost. From 2006 to 2013, the company’s annual cost was about $125 million. Is it possible the company had annual revenue of $160 million from 2006 to 2013? Explain.
Answer:
From part (a),
The total profit from 2006 to 2013 is:
P = 65 + 70 + 85 + 50 + 65 + 70 + 90
= $575 million
P = R – C to find the profit P, where R is the revenue and C is the cost.
It is also given that from 2006 to 2013, the company’s annual cost was about $125 million.
P = R – C
R = P + C
R = 575 + 125
= $700 million
Maintaining Mathematical Proficiency
Solve the equation. Graph the solutions, if possible.
Question 35.
| \(\frac{d}{9}\) | = 6
Answer:
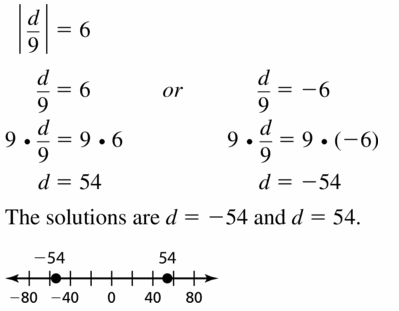
Question 36.
7 | 5p – 7 | = -21
Answer:
7 | 5p – 7 | = 21
| 5p – 7 | = -21 / 7
| 5p – 7 | = -3
| x | = x for x > 0
| x | = -x for x < 0
5p – 7 = -3 or 5p – 7 = – (-3)
5p = -3 + 7 or 5p = 3 + 7
5p = 4 or 5p = 10
p = \(\frac{4}{5}\) or p = 2
p = 0.8 or p = 2
p = 1 [Approx. value] or p = 2

Question 37.
| r + 2 | = | 3r – 4 |
Answer:
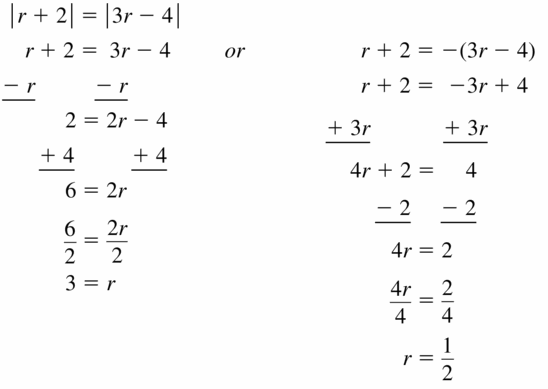
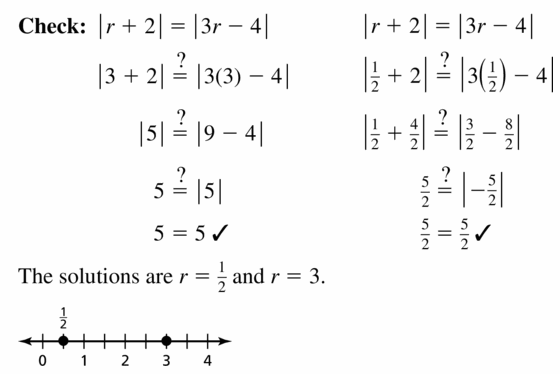
Question 38.
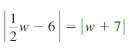
Answer:
| \(\frac{1}{2}\)w – 6 | = | w + 7 |
\(\frac{1}{2}\)w – 6 = w + 7
\(\frac{1}{2}\)w – w = 7 + 6
–\(\frac{1}{2}\)w = 13
w = 13 (-2)
w = -26
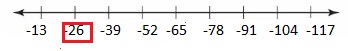
Find and interpret the mean absolute deviation of the data.
Question 39.
1, 1, 2, 5, 6, 8, 10, 12, 12, 13
Answer:
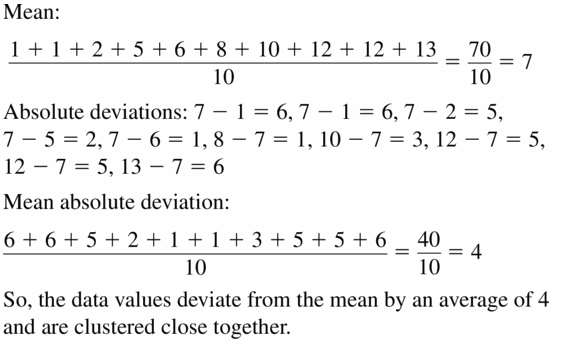
Question 40.
24, 26, 28, 28, 30, 30, 32, 32, 34, 36
Answer:
24, 26, 28, 28, 30, 30, 32, 32, 34, 36
Mean = \(\frac{The sum of the given numbers}{The total number of numbers}\)
= \(\frac{24 + 26+ 28 + 28 + 30 + 30 + 32 + 32 + 34 + 36}{10}\)
= \(\frac{300}{10}\)
= 30
Absolute deviation = ( The mean ) – ( Given number )
Absolute deviations are:
30 – 24, 30 – 26, 30 – 28, 30 – 28, 30 – 30, 30 – 30, 30 – 32, 30 – 32, 30 – 34, 30 – 36
= 6, 4, 2, 2, 0, 0, -2, -2, -6, -4
Absolute Mean deviation = \(\frac{Sum of Absolute deviations}{The number of absolute deviations}\)
= \(\frac{6 + 4 + 2 + 2 + 0 + 0 – 2 – 2 – 6 – 4}{10}\)
= \(\frac{0}{10}\)
= 0
Lesson 2.6 Solving Absolute Value Inequalities
Essential Question
How can you solve an absolute value inequality? Solving an Absolute Value Inequality Algebraically
EXPLORATION 1
Solving an Absolute Value Inequality Algebraically
Work with a partner.
Consider the absolute value inequality | x + 2 | ≤ 3.
a. Describe the values of x + 2 that make the inequality true. Use your description to write two linear inequalities that represent the solutions of the absolute value inequality.
b. Use the linear inequalities you wrote in part (a) to find the solutions of the absolute value inequality.

c. How can you use linear inequalities to solve an absolute value inequality?
Answer:
a.
| x | = x for x > 0
| x | = -x for x < 0
x + 2 ≤ 3 or x + 2 ≤ -3
x ≤ 3 – 2 or x ≤ -3 – 2
x ≤ 1 or x ≤ -5
b.
| x + 2 | ≤ 3
The solutions of the given absolute value equation are:
x ≤ 1 or x ≤ -5
| x | = x for x > 0
| x | = -x for x < 0
For x = 1,
| 1 + 2 | ≤ 3
| 3 | ≤ 3
3 ≤ 3
For x = -5,
| -5 + 2 | ≤ 3
| -3 | ≤ 3
3 ≤ 3
c.
The following are the steps to solve the absolute value inequality:
A) Isolate the absolute value expression on the left side of the inequality
B) If the number on the other side of the inequality sign is negative, then your equation either has no solution or all real numbers as solutions
C) Remove the absolute value bars by setting up a compound inequality
D) Solve the inequalities
EXPLORATION 2
Solving an Absolute Value Inequality Graphically
Work with a partner. Consider the absolute value inequality
| x + 2 | ≤ 3.
a. On a real number line, locate the point for which | x + 2 | ≤ 3
Answer:
The given absolute value inequality is
| x + 2 | ≤ 3
From Exploration 1,
The solutions of the absolute value inequality | x + 2 | ≤ 3 are
x ≤ 1 and x ≤ -5
The compound inequality of the solution of the given absolute value inequality is
x ≤ 1 ( Since the absolute value inequality can never be negative )
![]()
b. Locate the points that are within 3 units from the point you found in part (a). What do you notice about these points?
Answer:
The compound inequality that represents the solution of the given absolute value inequality is:
x ≤ 1
The points that are within 3 units from the point x ≤ 1, i.e., the given point + 3
1 + 3 = 4
The point we have to locate in the graph is:
x ≤ 4
![]()
c. How can you use a number line to solve an absolute value inequality?
Answer:
You begin the marking of the points on the number line by making them into separate equations and then solving them separately. An absolute value equation has no solution if the absolute value expression equals a negative number since an absolute value can never be negative. You can write an absolute value inequality as a compound value inequality
EXPLORATION 3
Solving an Absolute Value Inequality Numerically
Work with a partner.
Solving an Absolute Value Inequality Numerically
Work with a partner. Consider the absolute value inequality | x + 2 | ≤ 3.
a. Use a spreadsheet, as shown, to solve the absolute value inequality.
b. Compare the solutions you found using the spreadsheet with those you found in Explorations 1 and 2. What do you notice?
c. How can you use a spreadsheet to solve an absolute value inequality?
Answer:
Communicate Your Answer
Question 4.
How can you solve an absolute value inequality?
Answer:
To solve inequalities with absolute values, use a number line to see how far the absolute value is from zero. Isolate the absolute value expression on the left side of the inequality. If the number on the other side of the inequality sign is negative, your equation either has no solution or all real numbers as solutions. Use the sign of each side of your inequality to decide which of these cases holds.
Question 5.
What do you like or dislike about the algebraic, graphical, and numerical methods for solving an absolute value inequality? Give reasons for your answers.
Answer:
Use algebraic, graphical, and numerical methods for solving an absolute value inequality depending on the situation.
The algebraic and graphical methods for solving an absolute value inequality are useful when the size of the inequality is small i.e., have only one variable
2.6 Lesson
Monitoring Progress
Solve the inequality. Graph the solution, if possible
Question 1.
| x | ≤ 3.5
Answer:
| x | ≤ 3.5
| x | =x for x > 0
| x | = -x for x < 0
x ≤ 3.5
x ≤ 4 [Approximate value}
![]()
Question 2.
| k – 3 | < -1
Answer:
| k – 3 | < -1
If the number on the other side of the absolute value expression is negative, then the given absolute value equation has no solution or has real numbers as a solution
The given absolute value inequality has no solution
Question 3.
| 2w – 1 | < 11
Answer:
| 2w – 1 | < 11
| x | =x for x > 0
| x | = -x for x < 0
2w – 1 < 11
2w < 11 + 1
2w < 12
w < 12 / 2
w < 6
![]()
Question 4.
| x + 3 | > 8
Answer:
| x + 3 | > 8
| x | = x for x > 0
| x | = -x for x < 0
x + 3 > 8
x > 8 – 3
x > 5
![]()
Question 5.
| n + 2 | – 3 ≥ -6
Answer:
| n + 2 | – 3 ≥ -6
| n + 2 | ≥ -6 + 3
| n + 2 | ≥ -3
If the number on the other side of the absolute value expression is negative, then the given absolute value equation has no solution or has real numbers as a solution.
The given absolute value inequality has no solution.
Question 6.
3 | d + 1 | – 7 ≥ -1
Answer:
3 | d + 1 | – 7 ≥ -1
3 | d + 1 | ≥ -1 + 7
3 | d + 1 | ≥ 6
| d + 1 | ≥ 6 / 3
| d + 1 | ≥ 2
| x | = x for x > 0
| x | = -x for x < 0
d + 1 ≥ 2
d ≥ 2 – 1
d ≥ 1
![]()
Question 7.
WHAT IF?
You are willing to pay the mean price with an absolute deviation of at most $75. How many of the computer prices meet your condition?
Answer:
Solving Absolute Value Inequalities 2.6 Exercises
Question 1.
REASONING
Can you determine the solution of | 4x – 2 | ≥ -6 without solving it? Explain
Answer:
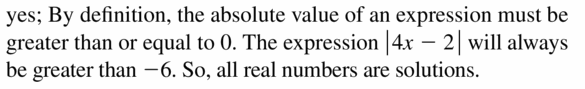
Question 2.
WRITING
Describe how solving | w – 9 | ≤ 2 is different from solving | w – 9 | ≥ 2.
Answer:
| w – 9 | ≤ 2 and | w – 9 | ≥ 2
| x | = x for x > 0
| x | = -x for x < 0
w – 9 ≤ 2 and w – 9 ≥ 2
w ≤ 2 + 9 and w ≥ 2 + 9
w ≤ 11 and w ≥ 11
w – 9 ≤ -2 and w – 9 ≥ -2
w ≤ -2 + 9 and w ≥ -2 + 9
w ≤ 7 and w ≥ 7
Monitoring Progress and Modeling with Mathematics
In Exercises 3–18, solve the inequality. Graph the solution, if possible.
Question 3.
| x | < 3
Answer:
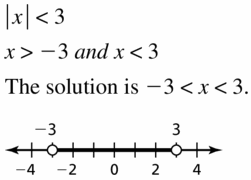
Question 4.
| y | ≥ 4.
Answer:
| y | ≥ 4
| x | = x for x > 0
| x | = -x for x < 0
y ≥ 4 or y ≤ -4
![]()
Question 5.
| d + 9 | > 3
Answer:
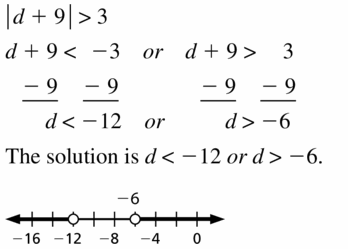
Question 6.
| h – 5 | ≤ 10
Answer:
| h – 5 | ≤ 10
| x | = x for x > 0
| x | = -x for x < 0
h – 5 ≤ 10
h ≤ 10 + 5 and h ≥ -10 + 5
h ≤ 15 and h ≥ -5
-5 ≤ h ≤ 15

Question 7.
| 2s – 7 | ≥ -1
Answer:
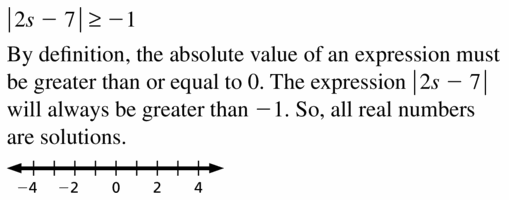
Question 8.
| 4c + 5 | > 7
Answer:
| 4c + 5 | > 7
| x | = x for x > 0
| x | = -x for x < 0
4c + 5 > 7 or 4c + 5 < -7
4c > 7 – 5 or 4c < -7 – 5
4c > 2 or 4c < -12
c > \(\frac{2}{4}\) or c < –\(\frac{4}{12}\)
c > \(\frac{1}{2}\) or c < –\(\frac{1}{3}\)
c > \(\frac{1}{2}\) or c < –\(\frac{1}{3}\)
c > 1 or c < 0 [ Approximate values of the inequality ]
![]()
Question 9.
| 5p + 2 | < -4
Answer:
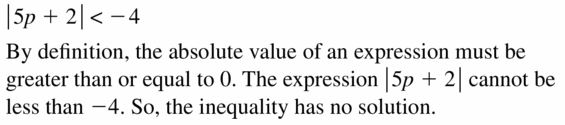
Question 10.
| 9 – 4n | < 5
Answer:
| 9 – 4n | < 5
| x | = x for x > 0
| x | = -x for x < 0
9 – 4n < 5 and 9 – 4n > -5
9 – 5 < 4n and 9 + 5 > 4n
4 < 4n and 14 > 4n
4n > 4 and 4n < 14
n > 4/ 4 and n < 14 / 4
n > 1 and n < 7 / 2
n > 1 and n < 3.5
1 < n < 3.5
![]()
Question 11.
| 6t – 7 | – 8 ≥ 3
Answer:
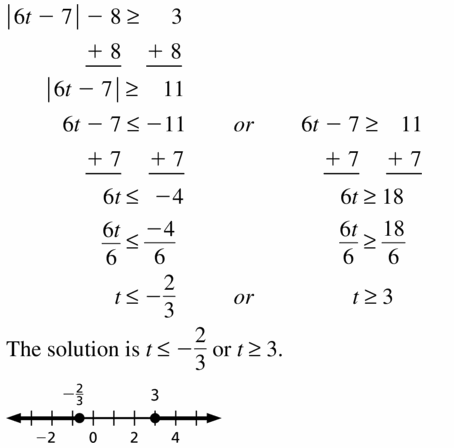
Question 12.
| 3j – 1 | + 6 > 0
Answer:
| 3j – 1 | + 6 > 0
| 3j – 1 | > 0 – 6
| 3j – 1 | > -6
The expression | 3j – 1 | will always be greater than -6
For the given absolute value inequality, all the real numbers are solutions
Question 13.
3 | 14 – m | > 18
Answer:
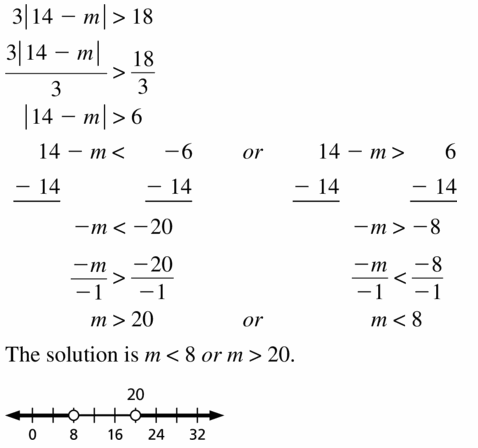
Question 14.
-4 | 6b – 8 | ≤ 12
Answer:
-4 | 6b – 8 | ≤ 12
| 6b – 8 | ≤ -3
The expression | 6b – 8 | must not be less than -3
For the given absolute value inequality, there is no solution
Question 15.
2 | 3w + 8 | ≥ 13
Answer:
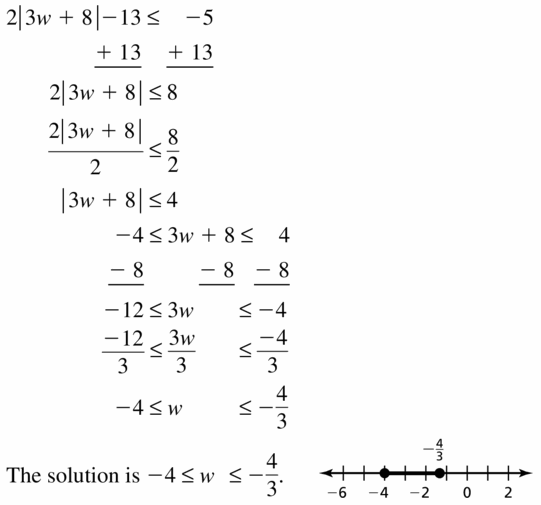
Question 16.
3 | 2 – 4u | + 5 < -13
Answer:
3 | 2 – 4u | + 5 < -13
3 | 2 – 4u | < -13 – 5
3 | 2 – 4u | < -18
| 2 – 4u | < -6
The expression | 2 – 4u | must not be less than -6
For the given absolute value inequality, there is no solution
Question 17.
6 | -f + 3 | + 7 > 7
Answer:
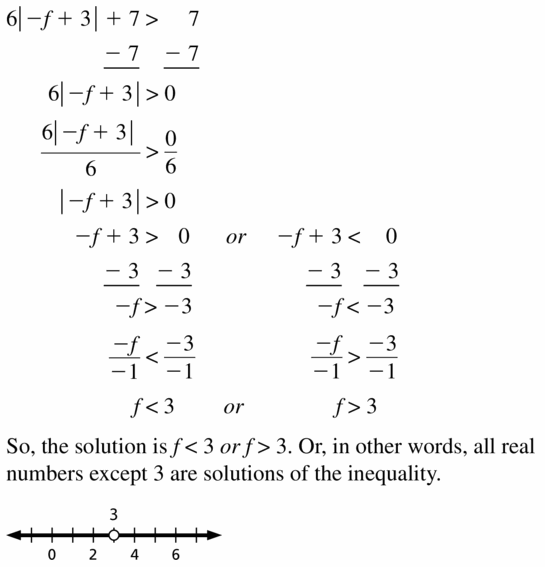
Question 18.
\(\frac{2}{3}\) |4v + 6 | – 2 ≤ 10
Answer:
\(\frac{2}{3}\) | 4v + 6 | – 2 ≤ 10
\(\frac{2}{3}\) | 4v + 6 | ≤ 10 + 2
\(\frac{2}{3}\) | 4v + 6 | ≤ 12
| 4v + 6 | ≤ 12 × \(\frac{3}{2}\)
| 4v + 6 | ≤ 18
| x | = x for x > 0
| x | = -x for x < 0
4v + 6 ≤ 18 and 4v + 6 ≥ -18
4v ≤ 18 – 6 and 4v ≥ -18 – 6
4v ≤ 12 and 4v ≥ -24
v ≤ 12 / 4 and v ≥ -24 / 4
v ≤ 3 and v ≥ -6
-6 ≤ v ≤ 3
![]()
Question 19.
MODELING WITH MATHEMATICS
The rules for an essay contest say that entries can have 500 words with an absolute deviation of at most 30 words. Write and solve an absolute value inequality that represents the acceptable numbers of words.
Answer:

Question 20.
MODELING WITH MATHEMATICS
The normal body temperature of a camel is 37°C. This temperature varies by up to 3°C throughout the day. Write and solve an absolute value inequality that represents the range of normal body temperatures (in degrees Celsius) of a camel throughout the day.

Answer:
The normal body temperature of a camel is 37°C and this temperature varies by up to 3°C throughout the day.
Let t be the temperature in °C
The absolute value inequality that represents the range of normal body temperatures of a camel throughout the day is:
37 – 3 ≤ t ≤ 37 + 3
34°C ≤ t ≤ 40°C
ERROR ANALYSIS
In Exercises 21 and 22, describe and correct the error in solving the absolute value inequality.
Question 21.

Answer:
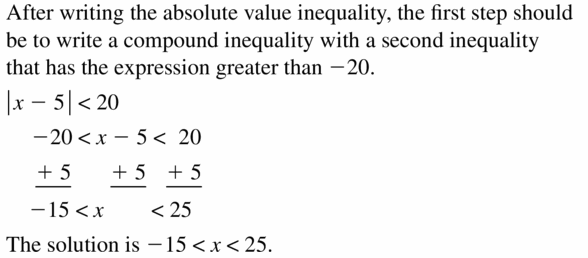
Question 22.
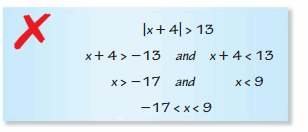
Answer:
| x + 4 | > 13
| x | = x for x > 0
| x | = -x for x < 0
x + 4 > 13 or x + 4 < -13
x > 13 – 4 or x < -13 – 4
x > 9 or x < -17
In Exercises 23–26, write the sentence as an absolute value inequality. Then solve the inequality.
Question 23.
A number is less than 6 units from 0.
Answer:
Question 24.
A number is more than 9 units from 3.
Answer:
A number is more than 9 units from 3
Let n be the number
| n – 3 | > 9
| x | = x for x > 0
| x | = -x for x < 0
n – 3 > 9 or n – 3 < -9
n > 9 + 3 or n < -9 + 3
n > 12 or n < -6
Question 25.
Half of a number is at most 5 units from 14.
Answer:
Question 26.
Twice a number is no less than 10 units from -1.
Answer:
Twice a number is no less than 10 units from -1
Let x be the number
| 2x – (-1) | > 10
| 2x + 1 | > 10
| x | = x for x > 0
| x | = -x for x < 0
2x + 1 > 10 or 2x + 1 < -10
2x > 10 – 1 or 2x < -10 – 1
2x > 9 or 2x < -11
x > \(\frac{9}{2}\) or x < –\(\frac{11}{2}\)
Question 27.
PROBLEM SOLVING
An auto parts manufacturer throws out gaskets with weights that are not within 0.06 pound of the mean weight of the batch. The weights (in pounds) of the gaskets in a batch are 0.58, 0.63, 0.65, 0.53, and 0.61. Which gasket(s) should be thrown out?
Answer:

Question 28.
PROBLEM-SOLVING
Six students measure the acceleration (in meters per second ) of an object in free fall. The measured values are shown. The students want to state that the absolute deviation of each measured value x from the mean is at most d. Find the value of d.
10.56, 9.52, 9.73, 9.80, 9.78, 10.91
Answer:
10.56, 9.52, 9.73, 9.80, 9.78, 10.91
Mean = \(\frac{Sum of the given observations}{Number of observations}\)
= \(\frac{10.56 + 9.52 + 9.73 + 9.80 + 9.78 + 10.91}{6}\)
= \(\frac{60.3}{6}\)
= 10.05
Absolute deviation = Mean – ( Given observation)
| x – 10.05 | ≤ d
| 10.56 – 10.05 | ≤ d
| 9.52 – 10.05 | ≤ d
| 9.73 – 10.05 | ≤ d
| 9.80 – 10.05 | ≤ d
| 9.78 – 10.05 | ≤ d
| 10.91 – 10.05 | ≤ d
d ≥ 0.51
d ≥ 0.53
d ≥ 0.32
d ≥ 0.25
d ≥ 0.27
d ≥ 0.86
The value of d is: 0.86
MATHEMATICAL CONNECTIONS
In Exercises 29 and 30, write an absolute value inequality that represents the situation. Then solve the inequality.
Question 29.
The difference between the areas of the figures is less than 2.
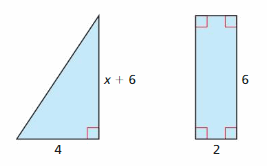
Answer:

Question 30.
The difference between the perimeters of the figures is less than or equal to 3.
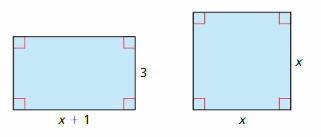
Answer:
The given figures are Rectangle and square
The perimeter of a rectangle = 2 ( Length + Width )
The perimeter of a square = 4 ( Side )
The perimeter of a rectangle = 2 ( 3 + x + 1 ) = 2 ( x + 4 )
The perimeter of a square = 4 (x) = 4x
It is given that the difference of the perimeters of the given figures is less than or equal to 3
| 2 ( x + 4 ) – 4x | ≤ 3
| x | = x for x > 0
| x | = -x for x < 0
2 (x + 4) – 4x ≤3 and 2 ( x + 4 ) – 4x ≥ -3
2x + 8 – 4x ≤ 3 and 2x + 8 – 4x ≥ -3
8 – 2x ≤ 3 and 8- 2x ≥ -3
-2x ≤ 3 – 8 and -2x ≥ -3 – 8
-2x ≤ -5 and -2x ≥ -11
2x ≤ 5 and 2x ≥ 11
x ≤ \(\frac{5}{2}\) and x ≥ \(\frac{11}{2}\)
REASONING
In Exercises 31–34, tell whether the statement is true or false. If it is false, explain why.
question 31.
If a is a solution of | x + 3 | ≤ 8, then a is also a solution of x + 3 ≥ -8.
Answer:
![]()
Question 32.
If a is a solution of | x + 3 | > 8, then a is also a solution of x + 3 > 8.
Answer:
If a is a solution of | x + 3 | > 8, then a is also a solution of x + 3 > 8
| x + 3 | > 8
| x | = x for x > 0
| x | = -x for x < 0
x + 3 > 8 or x + 3 < -8
The value of the absolute value expression must be greater than or equal to 0
x + 3 < -8 has no solution
a is a solution of x + 3 > 8
The statement is true.
Question 33.
If a is a solution of | x + 3 | ≥ 8, then a is also a solution of x + 3 ≥ -8.
Answer:
Question 34.
If a is a solution of x + 3 ≤ -8, then a is also a solution of | x + 3 | ≥ 8.
Answer:
If a is a solution of x + 3 ≤ -8, then a is a solution of | x + 3 | ≥ 8
The given absolute value inequality is:
| x + 3 | ≥ 8
| x | = x for x > 0
| x | = -x for x < 0
x + 3 ≥ 8 or x + 3 ≤ -8
If a is a solution of x + 3 ≥ 8, then a is also a solution of x + 3 ≤ -8
The statement is true
Question 35.
MAKING AN ARGUMENT
One of your classmates claims that the solution of | n | > 0 is all real numbers. Is your classmate correct? Explain your reasoning.
Answer:

Question 36.
THOUGHT-PROVOKING
Draw and label a geometric figure so that the perimeter P of the figure is a solution to the inequality | P – 60 | ≤ 12.
Answer:
| p – 60 | ≤ 12
| x | = x for x > 0
| x | = -x for x < 0
p – 60 ≤ 12 and p – 60 ≥ -12
p ≤ 12 + 60 and p ≥ -12 + 60
p ≤ 72 and p ≥ 48
The representation of the compound inequality of the perimeter of the figure is
48 ≤ p ≤ 72
Now, find the value of 4p i.e., the perimeter of the square
192 ≤ 4p ≤ 288
Question 37.
REASONING
What is the solution of the inequality | ax + b | < c, where c < 0? What is the solution of the inequality | ax + b | > c, where c < 0? Explain.
Answer:
Question 38.
HOW DO YOU SEE IT?
Write an absolute value inequality for each graph.
How did you decide which inequality symbol to use for each inequality?
Answer:
a. The 1st marked line starts from -1 including -1 and continued till the left end of the number line
The 2nd marked line starts from 5 including from 5 and continued till the right end of the number line
The representation of the marked lines in the form of absolute value inequality is
| x + 1 | ≤ 3 and | x – 5 | ≥ 1
b. The marked line starts from -1 excluding -1 and continued till 5 on the right end of the number line
The representation of the marked line in the form of absolute value inequality is
| x + 1 | > 6
c. The marked line starts from -1 including -1 and continued till 5 on the right end of the number line
The representation of the marked line in the form of absolute value inequality is
| x + 1 | ≥ 6
d. The 1st marked line starts from -1 excluding -1 and continued till the left end of the number line
The 2nd marked line starts from 5 excluding 5 and continued till the right end of the number line
The representation of the marked lines in the form of absolute value inequality is
| x + 1 | < 3 and | x – 5 | > 1
If the marked point is indicated on the number line and if that marked line continued till the right end of the number line, then we will use ≥
If the marked point is not indicated on the number line and if that marked line continued till the right end of the number line, then we will use >
If the marked point is indicated on the number line and if that marked line continued till the left end of the number line, then we will use ≤
If the marked point is not indicated on the number line and if that marked line continued till the left end of the number line, then we will use <
Question 39.
WRITING
Explain why the solution set of the inequality | x | < 5 is the intersection of two sets, while the solution set of the inequality | x | > 5 is the union of two sets.
Answer:

Question 40.
PROBLEM-SOLVING
Solve the compound inequality below. Describe your steps.
| x – 3 | < 4 and | x + 2 | > 8
Answer:
| x + 3 | < 4 and | x + 2 | > 8
| x | = x for x > 0
| x | = -x for x < 0
x + 3 < 4 or x + 3 > -4 and x + 2 > 8 or x + 2 < -8
x < 4 – 3 or x > -4 – 3 and x > 8 – 2 or x < -8 – 2
x < 1 or x > -7 and x > 6 or x < -10
-7 < x < 1 and -10 > x > 6
Maintaining Mathematical Proficiency
Plot the ordered pair in a coordinate plane. Describe the location of the point.
Question 41.
A(1, 3)
Answer:
Question 42.
B(0, -3)
Answer:
In the graph,
X-axis:
The right side of the x-axis will be: +ve
The left side of the x-axis will be: -ve
Y-axis:
The top side of the y-axis will be: +ve
The downside of the y-axis will be: -ve
B(0, -3) will be in the 4th Quadrant
The representation of point B in the graph is
Question 43.
C(-4, -2)
Answer:
Question 44.
D(-1, 2)
Answer:
X-axis:
The right side of the x-axis will be: +ve
The left side of the x-axis will be: -ve
Y-axis:
The top side of the y-axis will be: +ve
The downside of the y-axis will be: -ve
D(-1, 2) will be in the 2nd Quadrant
The representation of point D in the graph is
Copy and complete the table.
Question 45.
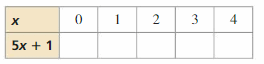
Answer:

Question 46.
Answer:
The completed table is:
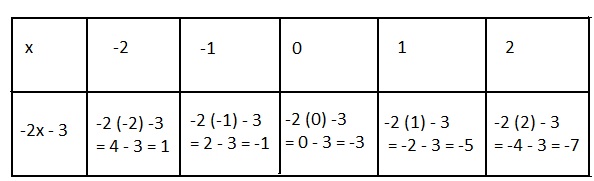
Solving Linear Inequalities Performance Task: Grading Calculations
2.5–2.6 What Did You Learn?
Core Vocabulary
compound inequality, p. 82
absolute value inequality, p. 88
absolute deviation, p. 90
Core Concepts
Section 2.5
Writing and Graphing Compound Inequalities, p. 82
Solving Compound Inequalities, p. 83
Section 2.6
Solving Absolute Value Inequalities, p. 88
Mathematical Practices
Question 1.
How can you use a diagram to help you solve Exercise 12 on page 85?
Answer:
In Exercise 12 on page 85,
The given diagram represents the maximum elevation of Mount Rainier
In the diagram,
The given maximum elevation of Mount Rainier is: 14,410 ft
So,
This 14,410 ft is divided into different types of elevation in Exercise 12
Question 2.
In Exercises 13 and 14 on page 85, how can you use structure to break down the compound inequality into two inequalities?
Answer:
In Exercises 13 and 14 on page 85,
First, perform the necessary mathematical operations so that only the variable must be present
After performing the necessary mathematical operations, the structure of the compound inequality will be like
a < x < b or a > x > b
The breakdown of the compound inequality a < x < b will be like x >a and x < b
The breakdown of the compound inequality a > x > b will be like x < a and x > b
We can put the different types of inequality symbols in the breakdown of inequalities
Question 3.
Describe the given information and the overall goal of Exercise 27 on page 91.
Answer:
An auto parts manufacturer throws out gaskets with weights that are not within 0.06 pounds of the mean weight of the batch. The weights (in pounds) of the gaskets in a batch are 0.58, 0.63, 0.65, 0.53, and 0.61
The overall goal of Exercise 27:
Find the mean of the given weights and find the absolute deviation of the gaskets
The absolute deviation of the gaskets that are less than 0.0 pounds of the man weight should be thrown out
Question 4.
For false statements in Exercises 31–34 on page 92, use examples to show the statements are false.
Answer:
In Exercises 31 – 34 on page 92,
Exercises 33 and 34 are false
The Exercise 33 is: | x + 3 | ≥ 8
The Exercise 34 is: | x + 3 | ≥ 8
In Exercise 33,
a is a solution for x + 3 ≥ 8 and x + 3 ≤ -8
In Exercise 34,
a is a solution of x + 3 ≥ 8 and x + 3 ≤ -8
Performance Task
Grading Calculations
You are not doing as well as you had hoped in one of your classes. So, you want to figure out the minimum grade you need on the final exam to receive the semester grade that you want. Is it still possible to get an A? How would you explain your calculations to a classmate?
To explore the answers to this question and more, go to 

Solving Linear Inequalities Chapter Review
2.1 Writing and Graphing Inequalities (pp. 53–60)
a. A number x plus 36 is no more than 40. Write this sentence as an inequality.
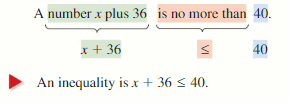
b. Graph w > −3.
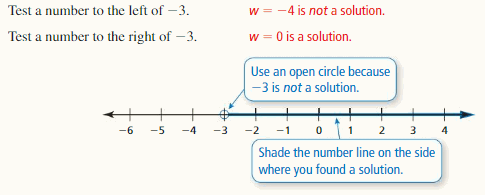
Write the sentence as an inequality.
Question 1.
A number d minus 2 is less than -1.
Answer:
A number d minus 2 is less than -1
The representation of the given worded form in the form of inequality is
d – 2 < -1
Question 2.
Ten is at least the product of a number h and 5.
Answer:
Ten is at least the product of a number h and 5
The representation of the given worded form in the form of inequality is
10 ≥ h(5)
10 ≥ 5h
10 / 5 ≥ h
2 ≥ h
h ≤ 2
Graph the inequality.
Question 3.
x > 4
Answer:
x > 4
![]()
Question 4.
y ≤ 2
Answer:
y ≤ 2
![]()
Question 5.
-1 ≥ z
Answer:
-1 ≥ z
z ≤ -1
![]()
2.2 Solving Inequalities Using Addition or Subtraction (pp. 61–66)
Solve x + 2.5 ≤ −6. Graph the solution.

Solve the inequality. Graph the solution.
Question 6.
p + 4 < 10
Answer:
p + 4 < 10
p < 10 – 4
p < 6
![]()
Question 7.
r – 4 < -6
Answer:
r – 4 < -6
r < -6 + 4
r < -2
![]()
Question 8.
2.1 ≥ m – 6.7
Answer:
2.1 ≥ m – 6.7
2.1 + 6.7 ≥ m
8.8 ≥ m
9 ≥ m [Approximate value]
m ≤ 9
![]()
2.3 Solving Inequalities. Using Multiplication or Division
Solve \(\frac{n}{-10}\) > 5. Graph the solution.

Solve the inequality. Graph the solution.
Question 9.
3x > -21
Answer:
3x > -21
x > -21 / 3
x > -7
![]()
Question 10.
-4 ≤ \(\frac{g}{5}\)
Answer:
-4 ≤ \(\frac{g}{5}\)
-4 (5) ≤ g
-20 ≤ g
g ≥ -20
![]()
Question 11.
–\(\frac{3}{4}\)n ≤ 3
Answer:
–\(\frac{3}{4}\)n ≤ 3
n ≤ 3 × –\(\frac{4}{3}\)
n ≤ –\(\frac{3 × 4}{3}\)
n ≤ -4
![]()
Question 12.
\(\frac{s}{-8}\) ≥ 11
Answer:
\(\frac{s}{-8}\) ≥ 11
s ≥ 11 (-8)
s ≥ -88
![]()
Question 13.
36 < 2q
Answer:
36 < 2q
So,
36 / 2 < q
18 < q
q > 18

Question 14.
-1.2k > 6
Answer:
-1.2k > 6
k > 6 / -1.2
k > -60 / 12
k > -5
![]()
2.4 Solving Multi-step Inequalities
Solve 22 + 3y ≥ 4. Graph the solution.

Solve the inequality. Graph the solution, if possible.
Question 15.
3x – 4 > 11
Answer:
3x – 4 > 11
3x > 11 + 4
3x > 15
x > 15 / 3
x > 5
![]()
Question 16.
-4 < \(\frac{b}{2}\) + 9
Answer:
-4 < \(\frac{b}{2}\) + 9
-4 – 9 < \(\frac{b}{2}\)
-13 < \(\frac{b}{2}\)
-13 (2) < b
-26 < b
b > -26
![]()
Question 17.
7 – 3n ≤ n + 3
Answer:
7 – 3n ≤ n + 3
-3n – n ≤ 3 – 7
-4n ≤ -4
4n ≤ 4
n ≤ 4 / 4
n ≤ 1
![]()
Question 18.
2(-4s + 2) ≥ -5s – 10
Answer:
2 (-4s +2) ≥ -5s – 10
2 (-4s) + 2 (2) ≥ -5s – 10
-8s + 4 ≥ -5s – 10
-8s + 5s ≥ -10 – 4
-3s ≥ -14
3s ≥ 14
s ≥ 14 / 3
s ≥ 5 [ Approximate value }
![]()
Question 19.
6(2t + 9) ≤ 12t – 1
Answer:
6(2t + 9) ≤ 12t – 1
6 (2t) + 6 (9) ≤ 12t – 1
12t + 54 ≤ 12t – 1
1t – 12t + 54 ≤ -1
54 ≤ -1
Question 20.
3r – 8 > 3(r – 6)
Answer:
3r – 8 > 3 ( r – 6 )
3r – 8 > 3 (r) – 3 (6)
3r – 8 > 3r – 18
3r – 8 – 3r > -18
-8 > -18
8 > 18
2.5 Solving Compound Inequalities
Solve −1 ≤ −2d + 7 ≤ 9. Graph the solution.

Question 21.
A number x is more than -6 and at most 8. Write this sentence as an inequality. Graph the inequality.
Answer:
A number x is more than -6 and at most 8
The representation of the given worded form in the form of inequality is
x > -6 and x ≤ 8
The representation of the solutions of the given worded form in the form of compound inequality is
-6 < x ≤ 8
![]()
Solve the inequality. Graph the solution.
Question 22.
19 ≥ 3z + 1 ≥ -5
Answer:
19 ≥ 3z + 1 ≥ -5
19 – 1 ≥ 3z + 1 – 1 ≥ -5 – 1
18 ≥ 3z ≥ -6
(18 / 3) ≥ (3z / 3) ≥ (-6 / 3)
6 ≥ z ≥ -2
-2 ≤ z ≤ 6
![]()
Question 23.
\(\frac{r}{4}\) < -5 or -2r – 7 ≤ 3
![]()
Answer:
\(\frac{r}{4}\) < -5 or -2r – 7 ≤ 3
r < -5 (4) or -2r ≤ 3 + 7
r < -20 or -2r ≤ 10
r < -20 or r ≤ -5
![]()
2.6 Solving Absolute Value Inequalities
Solve the inequality. Graph the solution, if possible.
Question 24.
| m | ≥ 10
Answer:
| m | ≥ 10
| x | = x for x > 0
| x | = -x for x < 0
m ≥ 10 or m ≤ -10
The value of the absolute value expression must be greater than or equal to 0
m ≥ 10
![]()
Question 25.
| k – 9 | < -4
Answer:
| k – 9 | < 4
| x | = x for x > 0
| x | = -x for x < 0
k – 9 < 4 and k – 9 > -4
k < 4 + 9 and k > -4 + 9
k < 13 and k > 5
5 < k < 13

Question 26.
4 | f – 6 | ≤ 12
Answer:
4 | f – 6 | ≤ 12
| f – 6 | ≤ 3
| x | = x for x > 0
| X | = -x for x < 0
f – 6 ≤ 3 and f – 6 ≥ -3
f ≤ 3 + 6 and f ≥ -3 + 6
f ≤ 9 and f ≥ 3
3 ≤ f ≤ 9
![]()
Question 27.
5 | b + 8 | – 7 > 13
Answer:
5 | b + 8 | – 7 > 13
5 | b + 8 | > 13 + 7
5 | b + 8 | > 20
| b + 8 | > 4
| x | = x for x > 0
| x | = -x for x < 0
b + 8 > 4 or b + 8 < -4
b > 4 + 8 or b < -4 – 8
b > 12 or b < -12
b > 12

Question 28.
| -3g – 2 | + 1 < 6
Answer:
| -3g – 2 | + 1 < 6
– | 3g + 2 | < 6 – 1
– | 3g + 2 | < 5
| 3g + 2 | < -5
Question 29.
| 9 – 2j | + 10 ≥ 2
Answer:
| 9 – 2j | + 10 ≥ 2
| 9 – 2j | ≥ 2 – 10
| 9 – 2j | ≥ -8
The value of the absolute value expression must be greater than or equal to 0
We can conclude that there is no solution to the given absolute value inequality
Question 30.
A safety regulation states that the height of a guardrail should be 106 centimeters with an absolute deviation of no more than 7 centimeters. Write and solve an absolute value inequality that represents the acceptable heights of a guardrail.
Answer:
A safety regulation states that the height of a guardrail should be 106 centimeters with an absolute deviation of no more than 7 centimeters.
Absolute deviation = ( Mean ) – ( The given observation )
Let the Mean be x
Absolute deviation = x – 106
| x – 106 | ≤ 7
| x | = x for x > 0
| x | = -x for x < 0
x – 106 ≤ 7 and x – 106 ≥ -7
x ≤ 7 + 106 and x ≥ -7 + 106
x ≤ 113 and x ≥ 99
| x – 106 | ≤ 7
Solving Linear Inequalities Chapter Test
Write the sentence as an inequality.
Question 1.
The sum of a number y and 9 is at least -1.
Answer:
The sum of a number y and 9 is at least -1
The representation of the given worded form in the form of inequality is:
y + 9 ≥ -1
Question 2.
A number r is more than 0 or less than or equal to -8.
Answer:
A number r is more than 0 or less than or equal to -8
The representation of the given worded form in the form of inequality is:
r > 0 or r ≤ -8
Question 3.
A number k is less than 3 units from 10.
Answer:
A number k is less than 3 units from 10
The representation of the given worded form in the form of inequality is:
k – 10 < 3
Solve the inequality. Graph the solution, if possible.
Question 4.
\(\frac{x}{2}\) – 5 ≥ -9
Answer:
\(\frac{x}{2}\) – 5 ≥ -9
\(\frac{x}{2}\) ≥ -9 + 5
\(\frac{x}{2}\) ≥ -4
x ≥ -4 (2)
x ≥ -8
![]()
Question 5.
-4s < 6s + 1
Answer:
-4s < 6s + 1
-4s – 6s < 1
-10s < 1
10s < -1
s < –\(\frac{1}{10}\)
s < -0.1

Question 6.
4p + 3 ≥ 2(2p + 1)
Answer:
4p + 3 ≥ 2 (2p + 1)
4p + 3 ≥ 2 (2p) + 2 (1)
4p + 3 ≥ 4p + 2
4p – 4p + 3 ≥ 2
3 ≥ 2
We can conclude that there is no solution for the given inequality
Question 7.
-7 < 2c – 1 < 10
Answer:
-7 < 2c – 1 < 10
-7 + 1 < 2c – 1 + 1 < 10 + 1
-6 < 2c < 11
(-6 / 2) < (2c / 2) < (11 / 2)
-3 < c < 5.5
-3 < c < 6 [Approximate inequality]
![]()
Question 8.
-2 ≤ 4 – 3a ≤ 13
Answer:
-2 ≤ 4 – 3a ≤ 13
-2 – 4 ≤ 4 – 4 – 3a ≤ 13 – 4
-6 ≤ -3a ≤ 9
6 ≥ 3a ≥ -9
(6 / 3) ≥ (3a / 3) ≥ (-9 / 3)
2 ≥ a ≥ -3
-3 ≤ a ≤ 2
![]()
Question 9.
-5 < 2 – h or 6h + 5 > 71
Answer:
-5 < 2 – h or 6h + 5 > 71
-5 – 2 < h or 6h > 71 – 5
-7 < -h or 6h > 66
7 < h or h > 66 / 6
h > 7 or h > 11

Question 10.
| 2q + 8 | > 4
Answer:
| 2q + 8 | > 4
| x | = x for x > 0
| x | = -x for x < 0
2q + 8 > 4 or 2q + 8 < -4
2q > 4 – 8 or 2q < -4 – 8
2q > -4 or 2q < -12
The given absolute value inequality has no solution
Question 11.
-2 | y – 3 | – 5 ≥ -4
Answer:
-2 | y – 3 | – 5 ≥ -4
-2 | y – 3 | ≥ -4 + 5
-2 | y – 3 | ≥1
| y – 3 | ≥ –\(\frac{1}{2}\)
The value of the absolute value expression must be greater than or equal to 0
The given absolute inequality has no solution
Question 12.
4 | -3b + 5 | – 9 < 7
Answer:
4 | -3b + 5 | – 9 < 7
4 | -3b + 5 | < 7 + 9
4 | -3b + 5 | < 16
| -3b + 5 | < 16 / 4
| -3b + 5 | < 4
| x | = x for x > 0
| x | = -x for x < 0
-3b + 5 < 4 and -3b + 5 > -4
-3b < 4 – 5 and -3b > -4 – 5
-3b < -1 and -3b > -9
3b < 1 and b > 3
b < \(\frac{1}{3}\) and b > 3
b < 0 and b > 3 [ Approximate value of inequality ]
![]()
Question 13.
You start a small baking business, and you want to earn a profit of at least $250 in the first month. The expenses in the first month are $155. What are the possible revenues that you need to earn to meet the profit goal?
Answer:
You start a small baking business, and you want to earn a profit of at least $250 in the first month. The expenses in the first month are $155.
P is the profit
R is the Revenue
E is the expenses
P = R – E
It is given that P ≥ $250
R – E ≥250
R – 155 ≥ 250
R ≥ 250 + 155
R ≥ 405
Question 14.
A manufacturer of bicycle parts requires that a bicycle chain have a width of 0.3 inches with an absolute deviation of at most 0.0003 inches. Write and solve an absolute value inequality that represents the acceptable widths.
Answer:
A manufacturer of bicycle parts requires that a bicycle chain have a width of 0.3 inches with an absolute deviation of at most 0.0003 inches.
Absolute deviation = Mean – Observation
Let the Mean be x
x – 0.3 ≤ 0.0003
The absolute value inequality that represents the acceptable widths is
| x – 0.3 | ≤ 0.0003
-0.0003 ≤ x – 0.3 ≤ 0.0003
-0.0003 + 0.3 ≤ x – 0.3 + 0.3 ≤ 0.0003 + 0.3
0.2997 ≤ x ≤ 0.3003
0.2997 inches ≤ w ≤0.3003 inches
Question 15.
Let a, b, c, and d be constants. Describe the possible solution sets of the inequality ax + b < cx + d.
Answer:
Write and graph a compound inequality that represents the numbers that are not solutions to the inequality represented by the graph shown. Explain your reasoning.
Question 16.
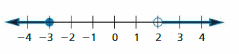
Answer:
The 1st marked line starts from -3 including -3 and continued till the left end of the number line
The 2nd marked line starts from 2 excluding 2 and continued till the right end of the number line
The representation of the inequalities from the graph is:
x ≤ -3 and x > 2
Question 17.

Answer:
The marked line starts from -4 including -4 and continued till -1 including -1 to the right end of the number line
The representation of the inequality from the graph is
x ≥ -4 and x ≤ -1
The representation of the inequalities in the form of compound inequality is
-4 ≤ x ≤ -1
Question 18.
A state imposes a sales tax on items of clothing that cost more than $175. The tax applies only to the difference in the price of the item and $175.
a. Use the receipt shown to find the tax rate (as a percent).
b. A shopper has $430 to spend on a winter coat. Write and solve an inequality to find the prices p of coats that the shopper can afford. Assume that p ≥ 175.
c. Another state imposes a 5% sales tax on the entire price of an item of clothing. For which prices would paying the 5% tax to be cheaper than paying the tax described above? Write and solve an inequality to find your answer and list three prices that are solutions.

Answer:
a. From the given receipt,
The price is: $295
The total price is: $302.50
Tax = Product price – $175
Let R be the tax rate
R (product price – 175) = 7.5
R ( 295 – 175 ) = 7.5
R ( 120 ) = 7.5
%R = \(\frac{7.5}{120}\) × 100
%R = \(\frac{75}{1200}\) × 100
%R = 0.0625 × 100
%R = 6.25%
b.
It is given that a shopper has $430 to spend on a winter coat
Let p be the number of coats
p ≥ 175
The total price = The given price + Tax
p + R ( p – 175 ) ≤ 430
p + 0.0625 (p – 175) ≤ 430
1.0625p – 10.9375 ≤ 430
1.0625p ≤ 430 + 10.9375
1.0625p ≤ 440.9375
p ≤ 440.9375 / 1.0625
p ≤ 415
c.
Given that another state imposes a 5% sales tax on the entire price of an item of clothing.
Let t be the tax rate that another state-imposed
Let x be the price
(1+0.05) × t ≤ t + 0.0625 (t – 175)
1.05t ≤ 1.0625t – 10.9375
10.9375 ≤ 1.0625t – 1.05t
10.9375 ≤ 0.0125t
10.9375 / 0.0125 ≤ t
875 ≤ t
t ≥ 875
$875 is cheaper
Solving Linear Inequalities Maintaining Cumulative Assessment
Question 1.
The expected attendance at a school event is 65 people. The actual attendance can vary by up to 30 people. Which equation can you use to find the minimum and maximum attendances?
A. | x – 65 | = 30
B. | x + 65 | = 30
C. | x – 30 | = 65
D. | x + 30 | = 65
Answer:
Given,
The expected attendance at a school event is 65 people.
The actual attendance can vary by up to 30 people.
The absolute value equation that represents the maximum and minimum attendances are
| x – Expected maximum attendance | ≤ 30
| x – 65 | ≤ 30
| x – 65 | = 30
We can conclude that option A represents the minimum and maximum attendance at a school event
Question 2.
Fill in values for a and b so that each statement is true for the inequality ax + 4 ≤ 3x + b.
a. When a = 5 and b = _____, x ≤ -3.
b. When a = _____ and b = _____, the solution of the inequality is all real numbers.
c. When a = _____ and b = _____, the inequality has no solution.
Answer:
a.
When a = 5,
5x + 4 ≤ 3x + b
5x – 3x + 4 ≤ b
2x + 4 ≤ b
2x ≤ b – 4
x ≤ ( b – 4 ) / 2
The solution x ≤ -3 will be possible only if b = -2
b.
ax + 4 ≤ 3x + b
Compare the like coefficients
The values of a and b so that the solution of an inequality is all real numbers are
a = 3, b ≥ 4
c.
ax + 4 ≤ 3x + b
The values of a and b so that the inequality has no solution are
a = 3 and b < 4
Question 3.
Place each inequality into one of the two categories.

Answer:
The inequalities that have at least one integer solution must have x variable
The inequalities that have no integer solution must not have x variable
a. 5x – 6 + x ≥ 2x – 8
b. x – 8 + 4x ≤ 3 (x – 3) + 2x
c. 2 (3x + 8) > 3 (2x + 6)
d. 9x – 3 < 12 or 6x + 2 > -10
e. 17 < 4x + 5 < 21
f. 5 (x – 1) ≤ 5x – 3
The inequalities that have at least one integer solution are: a, d, e
The inequalities that have no integer solution are: b, c, f
Question 4.
Admission to a play costs $25. A season pass costs $180.
a. Write an inequality that represents the number x of plays you must attend for the season pass to be a better deal.
b. Select the number of plays for which the season pass is not a better deal.

Answer:
a.
It is given that admission to a play costs $25 and a season pass costs $180
Let the number of plays be x
The total number of pays = 25x
The inequality that represents the number x of plays you must attend for the season pass to be a better deal is:
25x > 180
x > 180 / 25
x > 7.2
b.
From part (a),
The inequality that represents the season past to be a better deal is
x > 7.2
The inequality that represents the season pass not being a better deal is
x < 7.2
The number of plays that the season pass is not a better deal is: 0, 1, 2, 3, 4, 5, 6, and 7
Question 5.
Select the values of a that make the solution of the equation 3(2x – 4) = 4(ax – 2) positive.

Answer:
3 (2x – 4) = 4 (ax – 2)
3 (2x) – 3 (4) = 4 (ax) – 4 (2)
6x – 12 = 4ax – 8
6x – 12 + 8 = 4ax
6x – 4 = 4ax
6x – 4ax = 4
x (6 – 4a) = 4
The given numbers are: -2, -1, 0, 1, 2, 3, 4, 5
x (6 – 4(-2) ) = 4
x ( 6 – 4 ( -1) ) = 4
x ( 6 – 4(0) ) = 4
x ( 6 – 4(1) ) = 4
x ( 6 – 4 (2) ) = 4
x ( 6 – 4 (3) ) = 4
x ( 6 – 4 (4) ) = 4
x ( 6 – 4 (5) ) = 4
So, the values of a so that the solution is positive are: -2, -1, 0, 1
Question 6.
Fill in the compound inequality with <, ≤, , ≥, or > so the solution is shown in the graph.
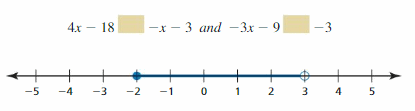
Answer:
-2 ≤ x < 3
4x – 18 ____ -x – 3 and -3x – 9 _____ -3
4x + x ____ -3 + 18 and -3x ___ -3 + 9
5x ____ 15 and -3x ___ 6
x ____ 15 / 5 and x ____ -3 / 6
x ____ 3 and x ____ -2
x < 3 and x ≥ -2
Question 7.
You have a $250 gift card to use at a sporting goods store.

a. Write an inequality that represents the possible numbers x of pairs of socks you can buy when you buy 2 pairs of sneakers. Can you buy 8 pairs of socks? Explain.
b. Describe what the inequality 60 + 80x ≤ 250 represents in this context.
Answer:
a.
The cost of a pair of sneakers is $80
The cost of a pair of socks is $12
It is given that there are 2 pairs of sneakers and x pairs of socks
2 (80) + 12x ≤ 250
160 + 12x ≤ 250
12x ≤ 250 – 160
12x ≤ 90
x ≤ 90 / 12
x ≤ 7.5
Thus you can buy only 7 pairs of socks
b.
60 + 8x ≤ 250
12 (5) + 8x ≤ 250
Thus you can buy 5 pairs of sneakers in this context
Question 8.
Consider the equation shown, where a, b, c, and d are integers.
ax + b = cx + d
Student A claims the equation will always have one solution. Student B claims the equation will always have no solution. Use the numbers shown to answer parts (a)–(c).

a. Select values for a, b, c, and d to create an equation that supports Student A’s claim.
Answer:
ax + b = cx + d
Student A claims the equation will have always one solution
The values of a, b, c, and d are
a = -1, b = 2, c = -1, d = 4
The value of x is:
-x + 2 = x + 4
-x – x = 4 – 2
-2x = 2
x = -2 /2
x = -1
The values of a, b, c, and d are
a = -1, b = 2, c = 1, d = 4
b. Select values for a, b, c, and d to create an equation that supports Student B’s claim.
Answer:
ax + b = cx + d
Student B claims that the equation will have no solution
The value of x must be equal to 0
a must be equal to c
The values of a, b, c, and d are: a = c and the values of b and d will be any number from the given numbers
c. Select values for a, b, c, and d to create an equation that shows both Student A and Student B are incorrect.
Answer:
ax + b = cx + d
For the claims of both Student A and Student B to be false,
The given equation must have the real numbers as a solution
To have the real numbers as a solution, the values of a and b will be arbitrary from the given numbers.