Big Ideas Math Book 6th Grade Advanced Answer Key Chapter 2 Fractions and Decimals
Fractions and Decimals STEAM Video/ Performance Task
STEAM Video

Space is Big
An astronomical unit (AU) is the average distance between Earth and the Sun, about 93 million miles. Why do asn000mers use astronomical units to measure distances in space? In what different ways can you compare the distances between objects and the locations of objects using the four mathematical operations?
Watch the STEAM Video ‘Space is Big: Then answer the following questions.
Question 1.
You know the distances between the Sun and each planet. How can you find the minimum and maximum distances between two planets as they rotate around the Sun?
Answer:
Question 2.
‘The table shows the distances of three celestial bodies from Earth. It takes about three days to travel from Earth to the Moon. I low can you estimate the amount of Lime it would take to travel from Earth to the Sun or to Venus?
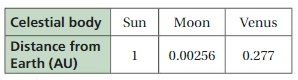
Answer:
Performance Task
Space Explorers

After completing this Chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task.
You will use a table that shows the average distances between the Sun and each planet in our solar system to find several distances in space. Then you will use the speed of the Orion spacecraft to answer questions about time and distance.
Is it realistic for a manned spacecraft to travel to each planet in our solar system? Explain why or why not.
Answer:
Getting Ready for Chapter Fractions and Decimals
Chapter Exploration
Work with a partner. ‘the area model represents the multiplication of two fractions. Copy and complete the statement.
Question 1.
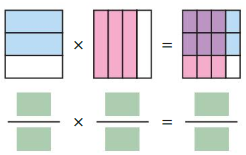
Answer:
Question 2.
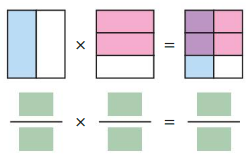
Answer:
Question 3.
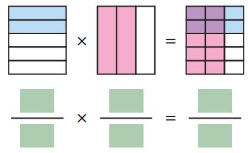
Answer:
Question 4.
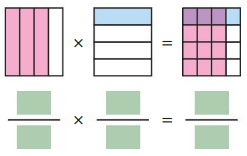
Answer:
Work with a partner. use an area model to find the product.
Question 5.
\(\frac{1}{2} \times \frac{1}{3}\)
Answer:
Question 6.
\(\frac{4}{5} \times \frac{1}{4}\)
Answer:
Question 7.
\(\frac{1}{6} \times \frac{3}{4}\)
Answer:
Question 8.
\(\frac{3}{5} \times \frac{1}{4}\)
Answer:
Question 9.
MODELING REAL LIFE
You have a recipe that serves 6 people. The recipe uses three-fourths of a cup of milk.

a. How can you use the recipe to serve more people? How much milk would you need? Give 2 examples.
Answer:
b. How can you use the recipe to serve fewer people? How much milk would you need? Give 2 examples.
Answer:
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
reciprocals multiplicative inverses
Answer:
Section 2.1 Multiplying Fractions
Exploration 1
Using Models to Solve a Problem
Work with a partner. A bottle of water is \(\frac { 1 }{ 2 }\) full. You drink \(\frac { 2 }{ 3 }\) the water. Use one of the models to find the portion of the bottle of water that you drink. Explain your steps.

number line
![]()
area model
tape diagram
![]()
Answer:
Exploration 2
Solving a Problem Involving Fractions
Work with a partner. A park has a playground that is \(\frac { 3 }{ 4 }\) of its width and \(\frac { 4 }{ 5 }\) of its length.
a. use a model to find the portion of the park that is covered by the playground. Explain your steps.
Answer:
b. How can you find the solution of part (a) without using a model?
Answer:
Math Practice
Find General Methods
How can you use your answer to find a method for multiplying fractions?
Answer:
Lesson 2.1 Multiplying Fractions
Try It MuItiply
Question 1.
\(\frac{1}{3} \times \frac{1}{5}\)
Answer:
Question 2.
\(\frac{2}{3} \times \frac{3}{4}\)
Answer:
Question 3.
\(\frac{1}{2} \cdot \frac{5}{6}\)
Answer:
Try It Multiply. Write the answer in simplest form.
Question 4.
\(\frac{3}{7} \times \frac{2}{3}\)
Answer:
Question 5.
\(\frac{4}{9} \cdot \frac{3}{10}\)
Answer:
Question 6.
\(\frac{6}{5} \cdot \frac{5}{8}\)
Answer:
Question 7.
WHAT IF?
You use \(\frac{1}{4}\) of the flour to make the dough. How much of the entire bag do you use to make the dough?
Answer:
Try It Multiply. Write the answer in simplest form.
Question 8.
\(\frac{1}{3} \times 1 \frac{1}{6}\)
Answer:
Question 9.
\(3 \frac{1}{2} \times \frac{4}{9}\)
Answer:
Question 10.
\(4 \frac{2}{3} \cdot \frac{3}{4}\)
Answer:
Try It Multiply. Write the answer in simplest form.
Question 11.
\(1 \frac{7}{8} \cdot 2 \frac{2}{5}\)
Answer:
Question 12.
\(5 \frac{5}{7} \times 2 \frac{1}{10}\)
Answer:
Question 13.
\(2 \frac{1}{3} \cdot 7 \frac{2}{3}\)
Answer:
MULTIPLYING FRACTIONS AND MIXED NUMBERS
Multiply. Write the answer in simplest form.
Question 14.
\(\frac{1}{8} \times \frac{1}{6}\)
Answer:
Question 15.
\(\frac{3}{8} \cdot \frac{2}{3}\)
Answer:
Question 16.
\(2 \frac{1}{6} \cdot 4 \frac{2}{5}\)
Answer:
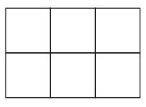
Question 17.
MP REASONING
What is the missing denominator?
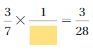
Answer:
Question 18.
USING TOOLS
Write a multiplication problem involving fractions that is represented by the model. Explain your reasoning.
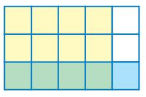
Answer:
Question 19.
USING TOOLS
Use the number line to find \(\frac{3}{4} \times \frac{1}{2}\) Explain your reasoning.
![]()
Answer:
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 20.
You spend \(\frac{5}{12}\) of a day at an amusement park. You spend \(\frac{2}{5}\) of that time riding waterslides. How many hours do you spend riding waterslides? Draw a model to show why your answer makes sense.
Answer:
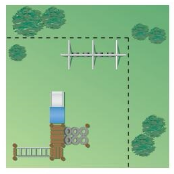
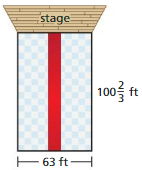
Question 21.
A venue is preparing for a concert on the floor shown. The width of the red carpet is \(\frac{1}{6}\) of the width of the floor. What is the area of the red carpet?

Answer:
Question 22.
You travel 9\(\frac{3}{8}\) miles from your house to a shopping mall. You travel \(\frac{2}{3}\) of that distance on an interstate. The only road construction you encounter is on the first \(\frac{2}{5}\) of the interstate. On how many miles of your trip do you encounter construction?
Answer:
Multiplying Fractions Practice 2.1
Review & Refresh
Find the LCM of the numbers.
Question 1.
8, 10
Answer:
Question 2.
5, 7
Answer:
Question 3.
2, 5, 7
Answer:
Question 4.
6, 7, 10
Answer:
Divide. Use a diagram to justify your answer.
Question 5.
6 ÷ \(\frac{1}{2}\)
Answer:
Question 6.
\(\frac{1}{4}\) ÷ 8
Answer:
Question 7.
4 ÷ \(\frac{1}{3}\)
Answer:
Question 8.
\(\frac{1}{5}\) ÷ 4
Answer:
Write the product as a power.
Question 9.
10 × 10 × 10
Answer:
Question 10.
5 × 5 × 5 × 5
Answer:
Question 11.
How many inches arc in 5\(\frac{1}{2}\) yards?
A. 15\(\frac{1}{2}\)
B. 16\(\frac{1}{2}\)
C. 66
D. 198
Answer:
Concepts, Skills, & Problem Solving
MP CHOOSE TOOLS
A bottle of water is \(\frac{2}{3}\) full. You drink the given portion of the water. Use a model to find the portion of the bottle of water that you drink.
Question 12.
\(\frac{1}{2}\)
Answer:
Question 13.
\(\frac{1}{4}\)
Answer:
Question 14.
\(\frac{3}{4}\)
Answer:
MULTIPLYING FRACTIONS
Multiply. Write the answer in simplest form.
Question 15.
\(\frac{1}{7} \times \frac{2}{3}\)
Answer:
Question 16.
\(\frac{5}{8} \cdot \frac{1}{2}\)
Answer:
Question 17.
\(\frac{1}{4} \times \frac{2}{5}\)
Answer:
Question 18.
\(\frac{3}{7} \times \frac{1}{4}\)
Answer:
Question 19.
\(\frac{2}{3} \times \frac{4}{7}\)
Answer:
Question 20.
\(\frac{5}{7} \times \frac{7}{8}\)
Answer:
Question 21.
\(\frac{3}{8} \cdot \frac{1}{9}\)
Answer:
Question 22.
\(\frac{5}{6} \cdot \frac{2}{5}\)
Answer:
Question 23.
\(\frac{5}{12}\) × 10
Answer:
Question 24.
6 • \(\frac{7}{8}\)
Answer:
Question 25.
\(\frac{3}{4} \times \frac{8}{15}\)
Answer:
Question 26.
\(\frac{4}{9} \times \frac{4}{5}\)
Answer:
Question 27.
\(\frac{3}{7} \cdot \frac{3}{7}\)
Answer:
Question 28.
\(\frac{5}{6} \times \frac{2}{9}\)
Answer:
Question 29.
\(\frac{13}{18} \times \frac{6}{7}\)
Answer:
Question 30.
\(\frac{7}{9} \cdot \frac{21}{10}\)
Answer:
Question 31.
MODELING REAL LIFE
In an aquarium, \(\frac{2}{5}\) of the fish are surgeonfish. of these, \(\frac{3}{4}\) are yellow tangs. What portion of all fish in the aquarium are yellow tangs?
Answer:
Question 32.
MODELING REAL LIFE
You exercise for \(\frac{3}{4}\) of an hour. You jump rope for \(\frac{1}{3}\) of that time. What portion of the hour do you spend jumping rope?
Answer:
MP REASONING
Without finding the products copy and complete the statement using <, >, or =. Explain your reasoning.
Question 33.
![]()
Answer:
Question 34.
![]()
Answer:
Question 35.
![]()
Answer:
MULTIPLYING FRACTIONS AND MIXED NUMBERS
Multiply. Write the answer in simplest form.
Question 36.
\(1 \frac{1}{3} \cdot \frac{2}{3}\)
Answer:
Question 37.
\(6 \frac{2}{3} \times \frac{3}{10}\)
Answer:
Question 38.
\(2 \frac{1}{2} \cdot \frac{4}{5}\)
Answer:
Question 39.
\(\frac{3}{5} \cdot 3 \frac{1}{3}\)
Answer:
Question 40.
\(7 \frac{1}{2} \times \frac{2}{3}\)
Answer:
Question 41.
\(\frac{5}{9} \times 3 \frac{3}{5}\)
Answer:
Question 42.
\(\frac{3}{4} \cdot 1 \frac{1}{3}\)
Answer:
Question 43.
\(3 \frac{3}{4} \times \frac{2}{5}\)
Answer:
Question 44.
\(4 \frac{3}{8} \cdot \frac{4}{5}\)
Answer:
Question 45.
\(\frac{3}{7} \times 2 \frac{5}{6}\)
Answer:
Question 46.
\(1 \frac{3}{10} \times 18\)
Answer:
Question 47.
\(15 \cdot 2 \frac{4}{9}\)
Answer:
Question 48.
\(1 \frac{1}{6} \times 6 \frac{3}{4}\)
Answer:
Question 49.
\(2 \frac{5}{12} \cdot 2 \frac{2}{3}\)
Answer:
Question 50.
\(5 \frac{5}{7} \cdot 3 \frac{1}{8}\)
Answer:
Question 51.
\(2 \frac{4}{5} \times 4 \frac{1}{16}\)
Answer:
YOU BE THE TEACHER
Your friend finds the product. Is your friend correct? Explain your reasoning.
Question 52.
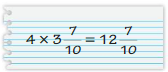
Question 53.

Question 54.
MODELING REAL LIFE
A vitamin C tablet contains \(\frac{1}{4}\) of a gram of vitamin C. You take 1\(\frac{1}{2}\) every day. How many grams of vitamin C do you take every day?
Question 55.
MP PROBLEM SOLVING
You make a banner for a football ralIy.

a. What is the area of the banner?
Answer:
b. You add a\(\frac{1}{4}\) foot border on each side. What is the area of the new banner?
Answer:
MULTIPLYING FRACTIONS AND MIXED NUMBERS
Multiply. Write the answer in simplest form.
Question 56.
\(\frac{1}{2} \times \frac{3}{5} \times \frac{4}{9}\)
Answer:
Question 57.
\(\frac{4}{7} \cdot 4 \frac{3}{8} \cdot \frac{5}{6}\)
Answer:
Question 58.
\(1 \frac{1}{15} \times 5 \frac{2}{5} \times 4 \frac{7}{12}\)
Answer:
Question 59.
\(\left(\frac{3}{5}\right)^{3}\)
Answer:
Question 60.
\(\left(\frac{4}{5}\right)^{2} \times\left(\frac{3}{4}\right)^{2}\)
Answer:
Question 61.
\(\left(\frac{5}{6}\right)^{2} \cdot\left(1 \frac{1}{10}\right)^{2}\)
Answer:
Question 62.
OPEN-ENDED
Find a fraction that, when multiplied by \(\frac{1}{2}\), is less than \(\frac{1}{4}\).
Answer:
Question 63.
MP LOGIC
You are in a bike race. When you get to the first checkpoint, you arc \(\frac{2}{5}\) of the distance to the second checkpoint. When you get to the second checkpoint, you are \(\frac{1}{4}\) of the distance to the finish. What is the distance from the start to the first checkpoint?

Answer:
Question 64.
MP NUMBER SENSE
Is the product of two positive mixed numbers ever less than 1? Explain.
Answer:
Question 65.
MP REASONING
You plan to add a fountain to your garden.
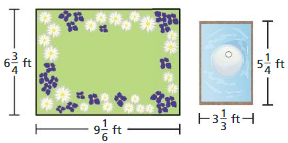
a. Draw a diagram o[thc fountain in the garden. Label the dimensions.
Answer:
b. Describe two methods for finding the area of the garden that surrounds the fountain.
Answer:
c. find the area. Which method did you use, and why?
Answer:
Question 66.
MP PROBLEM SOLVING
The cooking time for a ham is \(\frac{2}{5}\) of an hour for each pound. What time should you start cooking a ham that weighs 12\(\frac{3}{4}\) pounds so that it is done at 4:45 P.M. ?
Answer:
Question 67.
MP PRECISION
Complete the Four Square for \(\frac{7}{8} \times \frac{1}{3}\)
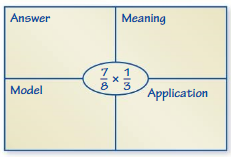
Answer:
Question 68.
DIG DEEPER!
You ask 150 people about their pets. The results show that \(\frac{9}{25}\) of the people own a dog. of the people who own a dog, \(\frac{1}{6}\) of them also own a cat.
a. What portion of the people own a dog and a cat?
Answer:
b. How many people own a dog but not a cat? Explain.
Answer:
Question 69.
MP NUMBER SENSE
Use each of the numbers from 1 to 9 exactly once to create three mixed numbers with the greatest possible product. then use each of the numbers exactly once to create three mixed numbers with the least possible product. Find each product. Explain your reasoning. The fraction portion of each mixed number should be proper.
![]()
Answer:
Section 2.2 Dividing Fractions
Exploration 1
Dividing by Fractions
Work with a partner. Answer each question using a model.

a. How many two-thirds arc in four?
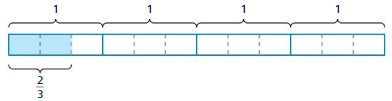
Answer:
b. How many three-fourths arc in three?
Answer:
c. How many two-fifths arc in four-fifths?
Answer:
d. How many two-thirds arc in three?
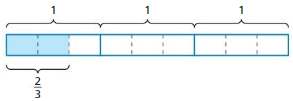
Answer:
e. How many one-thirds arc in five-sixths?
Exploration 2
Finding a Pattern
Work with a partner. The table shows the division expressions from Exploration 1. Complete each multiplication expression so that it has the same value as the division expression above it. What can you conclude about dividing by fractions?
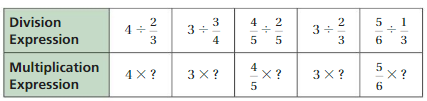
Answer:
Math Practice
Look for Structure
Can the pattern you found be applied to division by a whole number? Why or why not?
Answer:
Lesson 2.2 Dividing Fractions
Try It Write hie reciprocal of the number.
Question 1.
\(\frac{3}{4}\)
Answer:
Question 2.
5
Question 3.
\(\frac{7}{2}\)
Answer:
Question 4.
\(\frac{4}{9}\)
Answer:
Try It Divide. Write the answer in simplest form. Use a model to justify your answer.
Question 5.
\(\frac{1}{2} \div \frac{1}{8}\)
Answer:
Question 6.
\(\frac{2}{5} \div \frac{3}{10}\)
Answer:
Question 7.
\(\frac{3}{8} \div \frac{3}{4}\)
Answer:
Question 8.
\(\frac{2}{7} \div \frac{9}{14}\)
Answer:
Try It Divide. Write the answer in simplest form.
Question 9.
\(\frac{1}{3}\) ÷ 3
Answer:
Question 10.
\(\frac{2}{3}\) ÷ 10
Answer:
Question 11.
\(\frac{5}{8}\) ÷ 4
Answer:
Question 12.
\(\frac{6}{7}\) ÷ 4
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
DIVIDING FRACTIONS
Divide. Write the answer in simplest form. Draw a model to justify your answer.
Question 13.
\(\frac{2}{3} \div \frac{5}{6}\)
Answer:
Question 14.
\(\frac{6}{7}\) ÷ 3
Answer:
Question 15.
WHICH ONE DOESN’T BELONG?
Which of the following does not belong with the other three? Explain your reasoning.
\(\frac{2}{3} \div \frac{4}{5}\) \(\frac{3}{2} \cdot \frac{4}{5}\) \(\frac{5}{4} \times \frac{2}{3}\) \(\frac{5}{4} \div \frac{3}{2}\)
Answer:
MATCHING
Match the expression with its value.
| 16. \( \frac{2}{5} \div \frac{8}{15}\) | (A) \( \frac{1}{12}\) |
| 17. \( \frac{8}{15} \div \frac{2}{5}\) | (B) \( \frac{3}{4}\) |
| 18. \( \frac{2}{15} \div \frac{8}{5}\) | (c) 12 |
| 19. \( \frac{8}{5} \div \frac{2}{15}\) | (D) 1\( \frac{1}{3}\) |
Answer:
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding, of the success criteria in your journal.
Question 20.
You have 5 cups of rice to make bibimbap, a popular Korean meal. The recipe calls for \(\frac{4}{5}\) cup of rice per serving. H0w many full servings of bibimbap can you make? How much rice is left over?

Answer:
Question 21.
A band earns \(\frac{2}{3}\) of their profit from selling concert tickets and \(\frac{1}{5}\) of their profit from selling merchandise. The band earns a profit of $1500 from selling concert tickets. How much profit does the band earn from selling merchandise?

Answer:
Dividing Fractions Practice 2.2
Review & Refresh
Multiply. Write the answer in simplest form.
Question 1.
\(\frac{7}{10} \cdot \frac{3}{4}\)
Answer:
Question 2.
\(\frac{5}{6} \times 2 \frac{1}{3}\)
Answer:
Question 3.
\(\frac{4}{9} \times \frac{3}{8}\)
Answer:
Question 4.
\(2 \frac{2}{5} \cdot 6 \frac{2}{3}\)
Answer:
Match the expression with its value.
| 5. 3 + 2 × 42 | A. 22 |
| 6. (3 + 2) × 42 | B. 35 |
| 7. 2 + 3 × 42 | C. 50 |
| 8. 42 + 2 × 3 | D. 80 |
Answer:
Find the area of the rectangle.
Question 9.
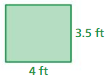
Answer:
Question 10.

Answer:
Question 11.

Answer:
Concepts, skills, & Problem Solving
CHOOSE TOOLS
Answer the question using a model. (See Exploration 1, Page.No 53.)
Question 12.
How many three-fifths are in three?
Answer:
Question 13.
How many two-ninths are in eight-ninths?
Answer:
Question 14.
How many three-fourths are in seven-eighths?
Answer:
WRITING RECIPROCALS
Write the reciprocal of the number.
Question 15.
8
Answer:
Question 16.
\(\frac{6}{7}\)
Answer:
Question 17.
\(\frac{2}{5}\)
Answer:
Question 18.
\(\frac{11}{8}\)
Answer:
DIVIDING FRACTIONS
Divide. Write the answer in simplest form.
Question 19.
\(\frac{1}{3} \div \frac{1}{2}\)
Answer:
Question 20.
\(\frac{1}{8} \div \frac{1}{4}\)
Answer:
Question 21.
\(\frac{2}{7} \div 2\)
Answer:
Question 22.
\(\frac{6}{5} \div 3\)
Answer:
Question 23.
\(\frac{2}{3} \div \frac{4}{9}\)
Answer:
Question 24.
\(\frac{5}{6} \div \frac{2}{7}\)
Answer:
Question 25.
\(12 \div \frac{3}{4}\)
Answer:
Question 26.
\(8 \div \frac{2}{5}\)
Answer:
Question 27.
\(\frac{3}{7} \div 6\)
Answer:
Question 28.
\(\frac{12}{25} \div 4\)
Answer:
Question 29.
\(\frac{2}{9} \div \frac{2}{3}\)
Answer:
Question 30.
\(\frac{8}{15} \div \frac{4}{5}\)
Answer:
Question 31.
\(\frac{1}{3} \div \frac{1}{9}\)
Answer:
Question 32.
\(\frac{7}{10} \div \frac{3}{8}\)
Answer:
Question 33.
\(\frac{14}{27} \div 7\)
Answer:
Question 34.
\(\frac{5}{8} \div 15\)
Answer:
Question 35.
\(\frac{27}{32} \div \frac{7}{8}\)
Answer:
Question 36.
\(\frac{4}{15} \div \frac{10}{13}\)
Answer:
Question 37.
\(9 \div \frac{4}{9}\)
Answer:
Question 38.
\(10 \div \frac{5}{12}\)
Answer:
YOU BE THE TEACHER
Your friend finds the quotient. Is your friend correct? Explain your reasoning.
Question 39.

Answer:
Question 40.

Answer:
Question 41.
MP REASONING
You have \(\frac{3}{5}\) of an apple pie. You divide the remaining pie into 5 equal slices. What portion of the original pie is each slice?
Answer:
Question 42.
MP PROBLEM SOLVING
How many times longer is the baby alligator than the baby gecko?
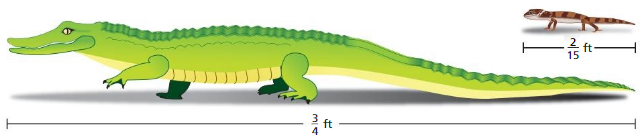
Answer:
OPEN-ENDED
Write a real-life problem for the expression. Then solve the problem.
Question 47.
![]()
Answer:
Question 48.
![]()
Answer:
Question 49.
![]()
Answer:
MP REASONING
Without finding the quotient, copy and complete the statement using <, >, or =. Explain your reasoning.
Question 50.
![]()
Answer:
Question 51.
![]()
Answer:
Question 52.
![]()
Answer:
Question 53.
![]()
Answer:
ORDER OF OPERATIONS
Evaluate the expression. Write the answer in simplest form.
Question 54.
\(\frac{1}{6}\) ÷ 6 ÷ 6
Answer:
Question 55.
\(\frac{7}{12}\) ÷ 14 ÷ 6
Answer:
Question 56.
\(\frac{3}{5} \div \frac{4}{7} \div \frac{9}{10}\)
Answer:
Question 57.
\(4 \div \frac{8}{9}-\frac{1}{2}\)
Answer:
Question 58.
\(\frac{3}{4}+\frac{5}{6} \div \frac{2}{3}\)
Answer:
Question 59.
\(\frac{7}{8}-\frac{3}{8} \div 9\)
Answer:
Question 60.
\(\frac{9}{16} \div \frac{3}{4} \cdot \frac{2}{13}\)
Answer:
Question 61.
\(\frac{3}{14} \cdot \frac{2}{5} \div \frac{6}{7}\)
Answer:
Question 62.
\(\frac{10}{27} \cdot\left(\frac{3}{8} \div \frac{5}{24}\right)\)
Answer:
Question 63.
MP NUMBER SENSE
When is the reciprocal of a fraction a whole number? Explain.
Answer:
Question 64.
MODELING REAL LIFE
You use \(\frac{1}{8}\) of your battery for every \(\frac{2}{5}\) of an hour that you video chat. You use \(\frac{3}{4}\) of your battery video chatting. How long did you video chat?
Answer:
Question 65.
MP PROBLEM SOLVING
The table shows the portions of a family budget that are spent on several expenses.
| Expense | Portion of Budget |
| Housing | \( \frac{2}{5}\) |
| Food | \( \frac{4}{9}\) |
| Automobiles | \( \frac{1}{15}\) |
| Recreation | \( \frac{1}{40}\) |
a. How many times more is the expense for housing than for automobiles?
Answer:
b. How many times more is the expense for food than for recreation?
Answer:
c. The expense for automobile fuel is \(\frac{1}{60} 0\) of the total expenses. What portion of the automobile expense is spent on fuel?
Answer:
Question 66.
CRITICAL THINKING
A bottle of juice is \(\frac{2}{3}\) full. the bottle contains \(\frac{4}{5}\) of a cup of juice.
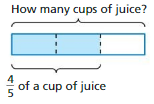
a. Write a division expression that represents the capacity of the bottle.
Answer:
b. Write a related multiplication expression that represents the capacity of the bottle.
Answer:
e. Explain how you can use the diagram to verify the expression In part (b).
Answer:
d. Find the capacity of the bade.
Answer:
Question 67.
DIG DEEPER!
You have 6 pints of glaze. It takes \(\frac{7}{8}\) of a pint to glaze a bowl and \(\frac{9}{16}\) of a pint to glaze a plate.

a. how many howls can you completely glaze? How many plates can you completely glaze?
Answer:
b. You want to glaze 5 bowls, and then use the rest for plates. How many plates can you completely glaze? How much glaze will be left over?
Answer:
c. How many of each object can you completely glaze so that there is no glaze left over? Explain how you found your answer.
Answer:
Question 68.
MP REASONING
A water tank is \(\frac{1}{8}\) full. The tank is \(\frac{3}{4}\) full when 42 gallons of water are added to the tank.

a. How much water can the tank hold?
Answer:
b. How much water was originally in the tank?
Answer:
c. How much water is in the tank when it is \(\frac{1}{2}\) full?
Answer:
Section 2.3 Dividing Mixed Numbers
Exploration 1
Dividing Mixed Numbers
Work with a partner. Write a real-life problem that represents each division expression described. Then solve each problem using a model. Check your answers.
a. How many three-fourths arc in four and one-half?

Answer:
b. How many three-eighths arc in two and one-fourth?
Answer:
c. How many one and one-halves arc in six?
Answer:
d. How many seven-sixths arc in three and one-third?

Answer:
e. How many one and one-fifths are in five?
Answer:
f. How many three and one-halves arc in two and one-half?
Answer:
g. How many four and one-halves arc in one and one-half?
Answer:
Lesson 2.3 Dividing Mixed Numbers
Try It Divide. Write the answer in simplest form.
Question 1.
\(3 \frac{2}{3} \div \frac{1}{3}\)
Answer:
Question 2.
\(1 \frac{3}{7} \div \frac{2}{3}\)
Answer:
Question 3.
\(2 \frac{1}{6} \div \frac{3}{4}\)
Answer:
Question 4.
\(6 \frac{1}{2} \div 2\)
Answer:
Question 5.
\(10 \frac{2}{3} \div 2 \frac{2}{3}\)
Answer:
Question 6.
\(8 \frac{1}{4} \div 1 \frac{1}{2}\)
Answer:
Question 7.
\(3 \div 1 \frac{3}{4}\)
Answer:
Question 8.
\(\frac{3}{4} \div 2 \frac{1}{2}\)
Answer:
Try It Evaluate the expression. Write the answer in simplest form.
Question 9.
\(1 \frac{1}{2} \div \frac{1}{6}-\frac{7}{8}\)
Answer:
Question 10.
\(3 \frac{1}{3} \div \frac{5}{6}+\frac{8}{9}\)
Answer:
Question 11.
\(\frac{2}{5}+2 \frac{4}{5} \div 2\)
Answer:
Question 12.
\(\frac{2}{5}+2 \frac{4}{5} \div 2\)
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
EVALUATING EXPRESSIONS
Evaluate the expression. Write the answer in simplest form.
Question 13.
\(4 \frac{4}{7} \div \frac{4}{7}\)
Answer:
Question 14.
\(\frac{1}{2} \div 5 \frac{1}{4}\)
Answer:
Question 15.
\(\frac{3}{4}+6 \frac{2}{5} \div 1 \frac{3}{5}\)
Answer:
Question 16.
MP NUMBER SENSE
Is \(2 \frac{1}{2} \div 1 \frac{1}{4}\) the sense as \(1 \frac{1}{4} \div 2 \frac{1}{2}\)? Use models to justify your answer.
Answer:
Question 17.
DIFFERENT WORDS. SAME QUESTION
Which is different? Find “b0th” answers.
What is 5\(\frac{1}{2}\) divided by \(\frac{1}{8}\)?
What is the quotient of 5\(\frac{1}{2}\) and \(\frac{1}{8}\)?
What is 5\(\frac{1}{2}\) times 8?
What is \(\frac{1}{8}\) of 5\(\frac{1}{2}\)?
Answer:
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
A water cooler contains 160 cups of water. During practice, each person on a team fills a water bottle with 3\(\frac{1}{3}\) cups of water from the cooler. Is there enough water for all 45 people on the team to fill their water bottles? Explain.
Answer:
Question 19.
A cyclist is 7\(\frac{3}{4}\) kilometers from the finish line of a race. The cyclist rides at a rate of 25\(\frac{5}{6}\) kilometers per hour. How many minutes will it take the cyclist to finish the race?

Answer:
Dividing Mixed Numbers Practice 2.3
Review & Refresh
Divide. Write the answer in simplest form.
Question 1.
\(\frac{1}{8} \div \frac{1}{7}\)
Answer:
Question 2.
\(\frac{7}{9} \div \frac{2}{3}\)
Answer:
Question 3.
\(\frac{5}{6}\) ÷ 10
Answer:
Question 4.
12 ÷ \(\frac{3}{8}\)
Answer:
Find the LCM of the numbers.
Question 5.
8, 14
Answer:
Question 6.
9, 11, 12
Answer:
Question 7.
12, 27, 30
Answer:
Find the volume of the rectangular prism.
Question 8.
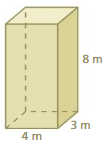
Answer:
Question 9.
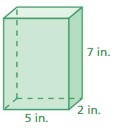
Answer:
Question 10.
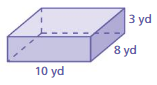
Answer:
Question 11.
Which number is not a prime factor of 286?
A. 2
B. 7
C. 11
D. 13
Answer:
Concepts, Skills & Problem Solving
MP CHOOSE TOOLS
Write a real-life problem that represents the division expression described. Then solve the problem using a model. Check your answer algebraically. (See Exploration 1, Page.No 61.)
Question 12.
How many two-thirds are in three and one-third?
Answer:
Question 13.
How many one and one-sixths are in five and five-sixths?
Answer:
Question 14.
How man two and one-halves are in eight and three-fourths?
Answer:
DIVIDING WITH MIXED NUMBERS
Divide. Write the answer in simplest form.
Question 15.
\(2 \frac{1}{4} \div \frac{3}{4}\)
Answer:
Question 16.
\(3 \frac{4}{5} \div \frac{2}{5}\)
Answer:
Question 17.
\(8 \frac{1}{8} \div \frac{5}{6}\)
Answer:
Question 18.
\(7 \frac{5}{9} \div \frac{4}{7}\)
Answer:
Question 19.
\(7 \frac{1}{2} \div 1 \frac{9}{10}\)
Answer:
Question 20.
\(3 \frac{3}{4} \div 2 \frac{1}{12}\)
Answer:
Question 21.
\(7 \frac{1}{5} \div 8\)
Answer:
Question 22.
\(8 \frac{4}{7} \div 15\)
Answer:
Question 23.
\(8 \frac{1}{3} \div \frac{2}{3}\)
Answer:
Question 24.
\(9 \frac{1}{6} \div \frac{5}{6}\)
Answer:
Question 25.
\(13 \div 10 \frac{5}{6}\)
Answer:
Question 26.
\(12 \div 5 \frac{9}{11}\)
Answer:
Question 27.
\(\frac{7}{8} \div 3 \frac{1}{16}\)
Answer:
Question 28.
\(\frac{4}{9} \div 1 \frac{7}{15}\)
Answer:
Question 29.
\(4 \frac{5}{16} \div 3 \frac{3}{8}\)
Answer:
Question 30.
\(6 \frac{2}{9} \div 5 \frac{5}{6}\)
Answer:
Question 31.
YOU BE THE TEACHER
Your friend finds the quotient of 3\(\frac{1}{2}\) and 1\(\frac{2}{3}\). Is your friend correct? Explain your reasoning.

Answer:
Question 32.
MP PROBLEM SOLVING
A platinum nugget weighs 3\(\frac{1}{2}\) ounces. How many \(\frac{1}{4}\) ounce pieces can he cut from the nugget?

Answer:
ORDER OF OPERATIONS
Evaluate the expression. Write the answer in simplest form.
Question 33.
\(3 \div 1 \frac{1}{5}+\frac{1}{2}\)
Answer:
Question 34.
\(4 \frac{2}{3}-1 \frac{1}{3} \div 2\)
Answer:
Question 35.
\(\frac{2}{5}+2 \frac{1}{6} \div \frac{5}{6}\)
Answer:
Question 36.
\(5 \frac{5}{6} \div 3 \frac{3}{4}-\frac{2}{9}\)
Answer:
Question 37.
\(6 \frac{1}{2}-\frac{7}{8} \div 5 \frac{11}{16}\)
Answer:
Question 38.
\(9 \frac{1}{6} \div 5+3 \frac{1}{3}\)
Answer:
Question 39.
\(3 \frac{3}{5}+4 \frac{4}{15} \div \frac{4}{9}\)
Answer:
Question 40.
\(\frac{3}{5} \times \frac{7}{12} \div 2 \frac{7}{10}\)
Answer:
Question 41.
\(4 \frac{3}{8} \div \frac{3}{4} \cdot \frac{4}{7}\)
Answer:
Question 42.
\(1 \frac{9}{11} \times 4 \frac{7}{12} \div \frac{2}{3}\)
Answer:
Question 43.
\(3 \frac{4}{15} \div\left(8 \cdot 6 \frac{3}{10}\right)\)
Answer:
Question 44.
\(2 \frac{5}{14} \div\left(2 \frac{5}{8} \times 1 \frac{3}{7}\right)\)
Answer:
Question 45.
MP LOGIC
Your friend uses the model shown to state that \(2 \frac{1}{2} \div 1 \frac{1}{6}=2 \frac{1}{6}\). Is your friend correct? Justify your answer using the model.
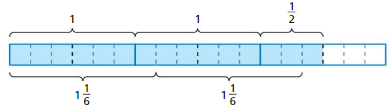
Answer:
Question 46.
MODELING REAL LIFE
A bag contains 42 cups of dog food. Your dog cats 2\(\frac{1}{3}\) cups of dog food each day. Is there enough food to last 3 weeks? Explain.

Answer:
Question 47.
DIG DEEPER!
You have 12 cups of granola and 8\(\frac{1}{2}\) cups of peanuts to make trail mix. What is the greatest number of full batches of trail mix you can make? Explain how you found your answer.

Answer:
Question 48.
MP REASONING
At a track and field meet, the longest shot-put throw by a boy is 25 feet 8 inches. the longest shot-put throw by a girl is 19 feet 3 inches. How many times greater is the longest shot-put throw by the boy than by the girl?
Answer: