Are you looking for the best preparation guide to practice geometry chapters? If yes, then refer to the Big Ideas Math Geometry Answers Chapter 5 Congruent Triangles guide. Enhance your Math Proficiency by preparing from the Big Ideas Math Book Geometry Solutions Chapter 5 Congruent Triangles PDF available. Here you can find all Chapter 5 Congruent Triangles Exercises questions and answers in a detail by our math experts. Download Big Ideas Math Geometry Answers of Ch 5 Congruent Triangles for free. Seek the Homework help you might need by accessing our Big Ideas Math Geometry Answers and clearing all your queries.
Big Ideas Math Book Geometry Answer Key Chapter 5 Congruent Triangles
Learn what is meant by Congruent Triangles from here. Two triangles are said to be congruent if three sides and the three angles are equal. Master the subject of Maths and get different questions from the Lessons, Exercises, Practice Tests, Chapter Reviews, Chapter Tests, and Cumulative Practice. Simply tap on the respective chapter and prepare whichever topic you feel is difficult and allot time accordingly. Test what you have learned from this chapter by solving the questions provided at the end of this chapter.
- Congruent Triangles Maintaining Mathematical Proficiency -Page 229
- Congruent Triangles Mathematical Practices – Page 230
- 5.1 Angles of Triangles – Page 231
- Lesson 5.1 Angles of Triangles – Page(232-238)
- Exercise 5.1 Angles of Triangles – Page(236-238)
- 5.2 Congruent Polygons – Page 239
- Lesson 5.2 Congruent Polygons – Page(240-244)
- Exercise 5.2 Congruent Polygons – Page(243-244)
- 5.3 Proving Triangle Congruence by SAS – Page 245
- Lesson 5.3 Proving Triangle Congruence by SAS – Page(246-250)
- Exercise 5.3 Proving Triangle Congruence by SAS – Page(249-250)
- 5.4 Equilateral and Isosceles Triangles – Page 251
- Lesson 5.4 Equilateral and Isosceles Triangles – Page(252-258)
- Exercise 5.4 Equilateral and Isosceles Triangles – Page(256-258)
- 5.1 to 5.4 Quiz – Page 260
- 5.5 Proving Triangle Congruence by SSS – Page 261
- Lesson 5.5 Proving Triangle Congruence by SSS – Page(262-268)
- Exercise 5.5 Proving Triangle Congruence by SSS – Page(266-268)
- 5.6 Proving Triangle Congruence by ASA and AAS – Page 269
- Lesson 5.6 Proving Triangle Congruence by ASA and AAS – Page(270-276)
- Lesson 5.6 Proving Triangle Congruence by ASA and AAS – Page(274-276)
- 5.7 Using Congruent Triangles – Page 277
- Lesson 5.7 Using Congruent Triangles – Page(278-282)
- Exercise 5.7 Using Congruent Triangles – Page(281-282)
- 5.8 Coordinate Proofs – Page 283
- Lesson 5.8 Coordinate Proofs – Page(284-288)
- Exercise 5.8 Coordinate Proofs – Page(287-288)
- Congruent Triangles Chapter Review – Page(290-294)
- Congruent Triangles Test – Page 295
- Congruent Triangles Cumulative Assessment – Page(296-297)
Congruent Triangles Maintaining Mathematical Proficiency
Find the coordinates of the midpoint M of the segment with the given endpoints. Then find the distance between the two points.
Question 1.
P(- 4, 1) and Q(0, 7)
Answer:
Given,
P (-4, 1), Q (0, 7)
The midpoint M of the segment with the 2 endpoints is:
( \(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\) )
Let the give points are:
(x1, y1) and (x2, y2)
x1 = -4, x2 = 0, y1 = 1, y2 = 7
The midpoint M = ( \(\frac{-4 + 0}{2}\), \(\frac{1 + 7}{2}\) )
= ( \(\frac{-4}{2}\), \(\frac{8}{2}\) )
= (-2, 4)
Question 2.
G(3, 6) and H(9, – 2)
Answer:
Given,
G (3, 6), H (9, -2)
The midpoint M of the segment with the 2 endpoints is:
( \(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\) )
(x1, y1) and (x2, y2)
x1 = 3, x2 = 9, y1 = 6, y2 = -2
Hence,
The midpoint M = ( \(\frac{3 + 9}{2}\), \(\frac{6 – 2}{2}\) )
= ( \(\frac{12}{2}\), \(\frac{4}{2}\) )
= (6, 2)
Question 3.
U(- 1, – 2) and V(8, 0)
Answer:
Given,
U (-1, -2), V (8, 0)
The midpoint M of the segment with the 2 endpoints is:
( \(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\) )
(x1, y1) and (x2, y2)
x1 = -1, x2 = 8, y1 = -2, y2 = 0
Hence,
The midpoint M = ( \(\frac{-1 + 8}{2}\), \(\frac{-2 + 0}{2}\) )
= ( \(\frac{7}{2}\), \(\frac{-2}{2}\) )
= ( \(\frac{7}{2}\), -1 )
Solve the equation.
Question 4.
7x + 12 = 3x
Answer:
Given,
7x + 12 = 3x
So,
7x – 3x = 12
4x = 12
x = \(\frac{12}{4}\)
x = 3
Question 5.
14 – 6t = t
Answer:
Given,
14 – 6t = t
So,
14 = 6t + t
7t = 14
t = \(\frac{14}{7}\)
t = 2
Question 6.
5p + 10 = 8p + 1
Answer:
Given,
5p + 10 = 8p + 1
5p – 8p = 1 – 10
-3p = -9
3p = 9
p = \(\frac{9}{3}\)
p = 3
Question 7.
w + 13 = 11w – 7
Answer:
Given,
w + 13 = 11w – 7
So,
w – 11w = -7 – 13
-10w = -20
10w = 20
w = \(\frac{20}{10}\)
w = 2
Question 8.
4x + 1 = 3 – 2x
Answer:
Given,
4x + 1 = 3 – 2x
So,
4x + 2x = 3 – 1
6x = 2
x = \(\frac{2}{6}\)
x = \(\frac{1}{3}\)
Question 9.
z – 2 = 4 + 9z
Answer:
Given,
z – 2 = 4 + 9z
So,
z – 9z = 4 + 2
-8z = 6
z = –\(\frac{6}{8}\)
z = –\(\frac{3}{4}\)
Question 10.
ABSTRACT REASONING
Is it possible to find the length of a segment in a coordinate plane without using the Distance Formula? Explain your reasoning.
Answer:
Yes, it is possible to find the length of a segment in a coordinate plane without using the distance formula.
Since the segment is a portion of a line, we can use the graph to calculate the distance of a segment even though it would not provide accurate results.
We use the distance formula to find the length of a segment in a coordinate plane
Congruent Triangles Mathematical Practices
Monitoring Progress
Classify each statement as a definition, a postulate, or a theorem. Explain your reasoning.
Question 1.
In a coordinate plane, two non-vertical lines are perpendicular if and only if the product of their slopes is – 1.
Answer:
Given,
In a coordinate plane, two non-vertical lines are perpendicular if and only if the product of their slopes is – 1.
According to the “parallel and perpendicular lines theorem”, two non-vertical lines are perpendicular if and only if the product of their slopes is -1.
The given statement is a Theorem
Question 2.
If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.
Answer:
Given,
If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.
According to the “Linear pair perpendicular theorem”,
When two straight lines intersect at a point and form a linear pair of congruent angles, then the lines are perpendicular
The given statement is a Theorem
Question 3.
If two lines intersect to form a right angle. then the lines are perpendicular.
Answer:
Given,
If two lines intersect to form a right angle. then the lines are perpendicular.
According to the “Perpendicular lines theorem”,
When two lines intersect to form a right angle, the lines are perpendicular
The given statement is a Theorem
Question 4.
Through any two points, there exists exactly one line.
Answer:
Given,
Through any two points, there exists exactly one line
Between two points, only one line can be drawn and we don’t need any proof to prove the above statement.
A statement that is true without proof to prove is called a “Postulate”
The given statement is a Postulate.
5.1 Angles of Triangles
Exploration 1
Writing a Conjecture
Work with a partner.
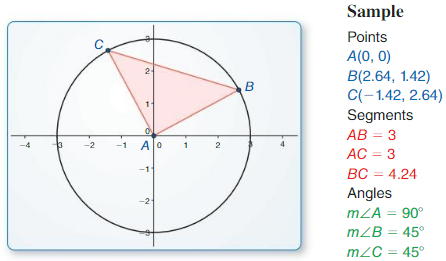
a. Use dynamic geometry software to draw any triangle and label it ∆ABC.
Answer:
By using the dynamic geometry software, the triangle drawn is:
b. Find the measures of the interior angles of the triangle.
Answer:
From part (a),
We can observe that the vertices of the triangle are: A, B, and C
Let the interior angles of the vertices A, B, and C be α, β, and γ respectively
The measures of the given triangle are:
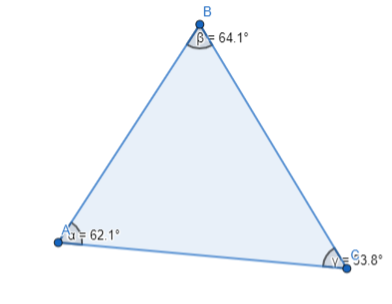
Hence, from the above,
The measures of the interior angles are:
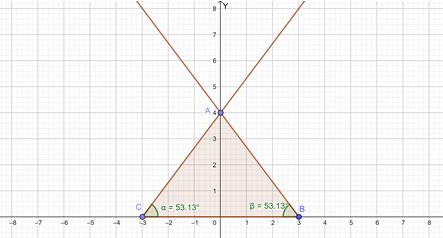
α = 62.1°, β = 64.1°, and γ = 53.8°
c. Find the sum of the interior angle measures.
Answer:
From part (b),
The measures of the interior angles are:
α = 62.1°, β = 64.1°, and γ = 53.8°
The sum of the interior angles = 62.1° + 64.1° + 53.1° = 180°
Hence, the sum of the interior angle measures is 180°
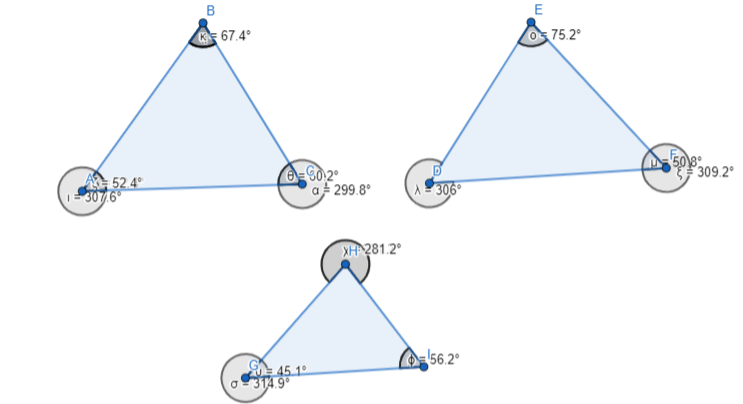
d. Repeat parts (a)-(c) with several other triangles. Then write a conjecture about the sum of the measures of the interior angles of a triangle.
Answer:
The representation of the 3 different triangles and their internal angle measures is:
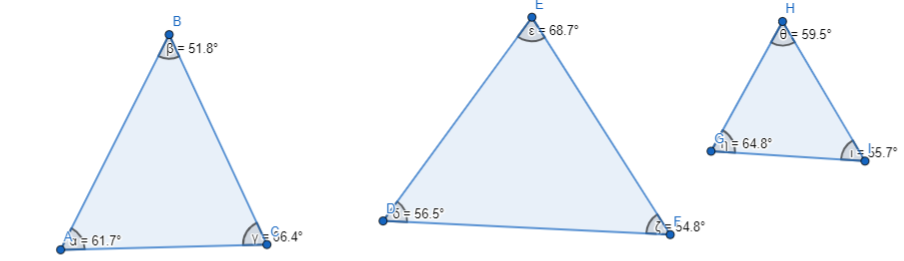
The sum of the internal angle measures of a triangle is always 180°
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to reason inductively about data and write conjectures.
Answer:
Inductive reasoning:
Inductive reasoning is the method of drawing conclusions based on a set of observations.
Inductive reasoning is used in geometry in a similar way.
Conjecture:
A statement you believe to be true based on inductive reasoning.
Exploration 2
Writing a Conjecture
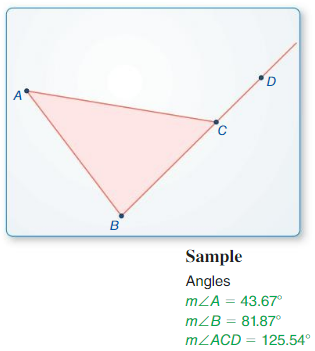
Work With a partner.
a. Use dynamic geometry software to draw any triangle and label it ∆ABC.
Answer:
The triangle drawn by using the dynamic geometry software is:
Hence, the vertices of the triangle are A, B, and C
b. Draw an exterior angle at any vertex and find its measure.
Answer:
From part (a),
The vertices of the triangle are: A, B, and C
Let the external angle measures of the triangle are: α, β, and γ
The representation of the external angle measures of the triangle are:
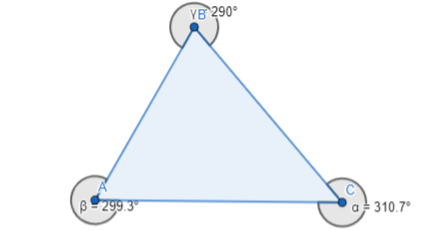
The external angle measures of the triangle are:
α = 310.7°, β = 299.3°, and γ = 290°
c. Find the measures of the two nonadjacent interior angles of the triangle.
Answer:
From part (b),
The external angle measures of the triangle are:
α = 310.7°, β = 299.3°, and γ = 290°
The representation of the non-adjacent interior angles and the external angle measures of the triangle are:
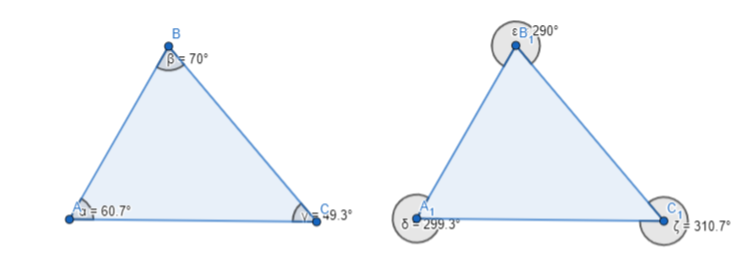
The angle measures of two non-adjacent sides are:
α = 70°, β = 60.7°, and γ = 49.3°
d. Find the sum of the measures of the two nonadjacent interior angles. Compare this sum to the measure of the exterior angle.
Answer:
The external angle measures of the triangle are:
α = 310.7°, β = 299.3°, and γ = 290°
The measures of the two non-adjacent interior angles are:
α = 70°, β = 60.7°, and γ = 49.3°
The sum of the measures of the external angles of the triangle are:
α + β + γ = 310.7° + 299.3°+ 290°
= 900.0°
The sum of the measures of the two non-adjacent interior angles is:
α + β + γ = 70° + 60.7° + 49.3°
= 180.0
We can conclude that the sum of the measures of the external angles is 5 times the sum of the measures of the two non-adjacent interior angles
e. Repeat parts (a)-(d) with several other triangles. Then write a conjecture that compares the measure of an exterior angle with the sum of the measures of the two nonadjacent interior angles.
Answer:
The external angle measure of a vertex for a given triangle = 360° – (Internal angle measure of a vertex that we are finding the external angle measure)
The sum of the internal angle measures of the triangle is 180°
Communicate Your Answer
Question 3.
How are the angle measures of a triangle related?
Answer:
The external angle measure of a vertex for a given triangle = 360° – (Internal angle measure of a vertex that we are finding the external angle measure)
The sum of the internal angle measures of the triangle is 180°
Question 4.
An exterior angle of a triangle measures 32° What do you know about the measures of the interior angles? Explain your reasoning.
Answer:
It is given that an exterior angle of a triangle measures 32°
The external angle measure of a vertex for a given triangle = 360° – (Internal angle measure of a vertex that we are finding the external angle measure)
32° = 360° – (The internal angle measure of 32°)
The internal angle measure of 32° = 360° – 32°
The interior angle measure of 32° = 328°
We can conclude that the interior angle measure of a triangle for an external angle measure of 32° is 328°
Lesson 5.1 Angles of Triangles
Monitoring Progress
Question 1.
Draw an obtuse isosceles triangle and an acute scalene triangle.
Answer:
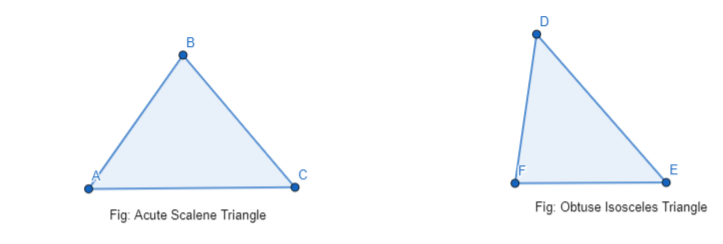
Question 2.
∆ABC has vertices A(0, 0), B(3, 3), and C(- 3, 3), Classify the triangle by its sides. Then determine whether it is a right triangle.
Answer:
Given,
A (0, 0), B (3, 3), and C (-3, 3)
AC² = AB² + BC²
The distance between 2 points = √(x2 – x1)² + (y2 – y1)²
Let the given points be considered as A(x1, y1), B(x2, y2), and C( x3, y3)
AB = √(3 – 0)² + (3 – 0)² = √3² + 3²
= √9 + 9 = √18
BC = √(-3 – 3)² + (3 – 3)²
= √(-6)² + 0²
= √6² = 6
AC = √(-3 – 0)² + (3 – 0)²
= √(-3)² + 3²
= √9 + 9 = √18
AC² = AB² + BC²
(√18)² = (√18)² + 6²
18 = 18 + 36
18 ≠54
We can conclude that the given triangle is not a right-angled triangle
Question 3.
Find the measure of ∠1
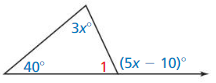
Answer:
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles
The exterior angle is: (5x – 10)°
The interior angles are: 40°, 3x°, ∠1
(5x – 10)° = 40° + 3x°
5x° – 3x° = 40° + 10°
2x° = 50°
x = 50° ÷ 2
x = 25°
So,
The interior angles are 40°, 3 (25)°, ∠1
= 40°, 75°, ∠1
The sum of the interior angles of a triangle is 180°
40° + 75° + ∠1 = 180°
115° + ∠1 = 180°
∠1 = 180° – 115°
∠1 = 65°
Question 4.
Find the measure of each acute angle.
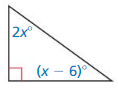
Answer:
The sum of the interior angles in a triangle is 180°
The interior angles of the right-angled triangle are: 90°, 2x°, and (x – 6)°
90° + 2x° + (x – 6)° = 180°
84°+ 3x° = 180°
3x° = 180° – 84°
3x° = 96°
x = 96° ÷ 3°
x = 32°
The measure of each acute angle is 90°, 2x°, (x – 6)°
= 90°, 2(32)°, (32 – 6)°
= 90°, 64°, 26°
The measure of each acute angle is 90°, 64°, and 26°
Exercise 5.1 Angles of Triangles
Vocabulary and Core Concept Check
Question 1.
WRITING
Can a right triangle also be obtuse? Explain our reasoning.
Answer:

Question 2.
COMPLETE THE SENTENCE
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two ____________ interior angles.
Answer:
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, classify the triangle by its sides and by measuring its angles.
Question 3.
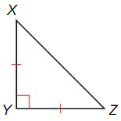
Answer:
Question 4.
Answer:
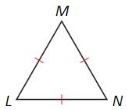
“|” represents the “Congruent” or “Equal” in geometry
We can observe that all three sides of the given triangle are equal.
If a triangle has all the sides equal, then the triangle is called an “Equilateral triangle”
ΔLMN is an “Equilateral triangle”
Question 5.
Answer:

Question 6.

Answer:
If any side is not equal to the other in the triangle, then the triangle is called a “Scalene triangle”
An angle greater than 90° is called as “Obtuse angle”
An angle less than 90° is called an “Acute angle”
ΔABC is an “Acute scalene triangle”
In Exercises 7-10, classify ∆ABC by its sides. Then determine whether it is a right triangle.
Question 7.
A(2, 3), B(6, 3), (2, 7)
Answer:

Question 8.
A(3, 3), B(6, 9), (6, – 3)
Answer:
Given,
A (3, 3), B(6, 9), and C (6, -3)
To find whether the given triangle is a right angle or not,
AC² = AB² + BC²
A (x1, y1), B(x2, y2), and C (x3, y3)
So,
A (x1, y1)= (3, 3), B (x2, y2) = (6, 9), and C (x3, y3) = (6, -3)
The distance between 2 points = √(x2 – x1)² + (y2 – y1)²
AB = √(6 – 3)² + (9 – 3)²
= √3² + 6²
= √9 + 36 = √45
BC = √6 – 6)² + (-3 – 9)²
= √0 + 12²
= √12² = 12
AC = √(6 – 3)² + (-3 – 3)²
= √(3)² + (-6)²
= √9 + 36 = √45
Slope (m) = \(\frac{y2 – y1} {x2 – x1}\)
So,
Slope of AB = \(\frac{9 – 3} {6 – 3}\)
= \(\frac{6} {3}\)
= 2
Slope of BC = \(\frac{-9 – 3} {6 – 6}\)
= \(\frac{-12} {0}\)
= Undefined
Slope of AC = \(\frac{-3 – 3} {6 – 3}\)
= \(\frac{-6} {3}\)
= -2
We can conclude that the given triangle is not a right triangle
Question 9.
A(1, 9), B(4, 8), C(2, 5)
Answer:

Question 10.
A(- 2, 3), B(0, – 3), C(3, – 2)
Answer:
Given,
A (-2, 3), B(0, -3), and C (3, -2)
AC² = AB² + BC²
The slope of any one side must be equal to -1
A (x1, y1), B(x2, y2), and C (x3, y3)
A (x1, y1)= (-2, 3), B (x2, y2) = (0, -3), and C (x3, y3) = (3, -2)
The distance between 2 points = √(x2 – x1)² + (y2 – y1)²
So,
AB = √(0 – [-2])² + (3 – 3)²
= √2² + 0²
= √4 + 0 = 2
BC = √3 – 0)² + (-2 -[-3] )²
= √9 + 1²
= √10
AC = √(3 – [-2])² + (-2 – 3)²
= √(5)² + (-5)²
= √25 + 25 = √50
Now,
AC² = AB² + BC²
50 = 10 + 4
50 ≠ 14
Slope (m) = \(\frac{y2 – y1} {x2 – x1}\)
Slope of AB = \(\frac{9 – 3} {6 – 3}\)
= \(\frac{6} {3}\)
= 2
Slope of BC = \(\frac{-9 – 3} {6 – 6}\)
= \(\frac{-12} {0}\)
= Undefined
Slope of AC = \(\frac{-3 – 3} {6 – 3}\)
= \(\frac{-6} {3}\)
= -2
We can conclude that the given triangle is not a right triangle
In Exercises 11 – 14. find m∠1. Then classify the triangle by its angles
Question 11.
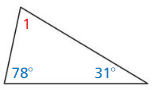
Answer:
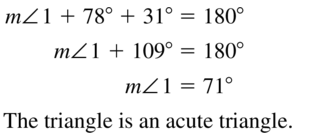
Question 12.
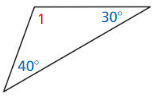
Answer:
The sum of interior angles in a triangle is 180°
The interior angles of the given triangle are: 40°, 30°, ∠1
40° + 30° + ∠1 = 180°
70 + ∠1 = 180°
∠1 = 180° – 70°
∠1 = 110°
The angle greater than 90° is called an “Obtuse angle”
We can conclude that the given triangle is an “Obtuse angled triangle”
Question 13.
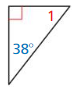
Answer:
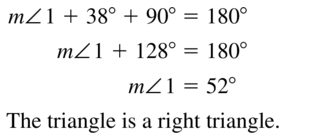
Question 14.
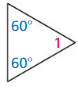
Answer:
The sum of interior angles in a triangle is 180°
The interior angles of the given triangle are 60°, 60°, ∠1
60° + 60° + ∠1 = 180°
120 + ∠1 = 180°
∠1 = 180° – 120°
∠1 = 60°
An angle less than 90° is called an “Acute angle”
The triangle that all the angles 60° is called an “Equilateral triangle”
In Exercises 15-18, find the measure of the exterior angle.
Question 15.
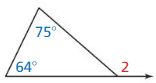
Answer:
![]()
Question 16.
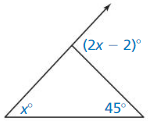
Answer:
An exterior angle is equal to the sum of the two non-adjacent interior angles in a triangle
(2x – 2)° = x° + 45°
2x° – x° = 45° + 2°
x = 47°
The measure of the exterior angle is: (2x – 2)°
= (2 (47) – 2)°
= (94 – 2)°
= 92°
Hence, the measure of the exterior angle is: 92°
Question 17.
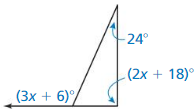
Answer:
Question 18.
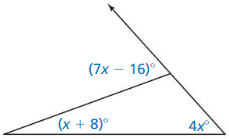
Answer:
An exterior angle is equal to the sum of the two non-adjacent interior angles in a triangle
(7x – 16)° = (x + 8)° + 4x°
7x° – 5x° = 16° + 8°
2x = 24°
x = 24° ÷ 2
x = 12°
The measure of the exterior angle is: (7x – 16)°
= (7 (12) – 16)°
= (84 – 16)°
= 68°
Hence, the measure of the exterior angle is: 68°
In Exercises 19-22, find the measure of each acute angle.
Question 19.
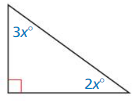
Answer:
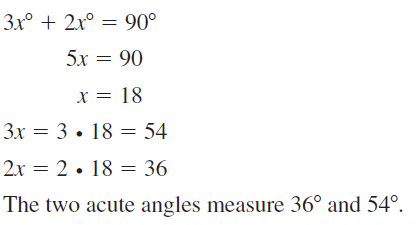
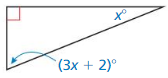
Question 20.
Answer:
x° + (3x + 2)° + 90° = 180°
4x° + 2° + 90° = 180°
4x° = 180° – 90° – 2°
4x° = 88°
x = 88° ÷ 4°
x = 22°
The 2 acute angle measures are: x° and (3x + 2)°
= 22° and (3(22) + 2)°
= 22° and (66 + 2)°
= 22° and 68°
Question 21.
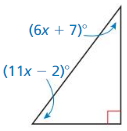
Answer:
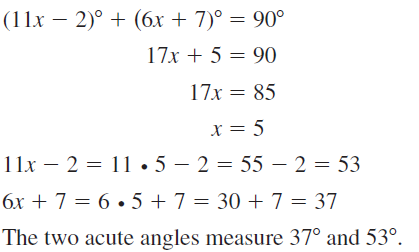
Question 22.
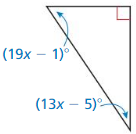
Answer:
(19x – 1)° + (13x – 5)° + 90° = 180°
32x° – 6° + 90° = 180°
32x° = 180° – 90° – 6°
4x° = 84°
x = 84° ÷ 4°
x = 21°
The 2 acute angle measures are: (19x – 1)° and (13x – 5)°
= (19 (21) – 1)° and (13(21) – 5)°
= 398° and (273 – 5)°
= 398° and 268°
In Exercises 23-26. find the measure of each acute angle in the right triangle.
Question 23.
The measure of one acute angle is 5 times the measure of the other acute angle.
Answer:
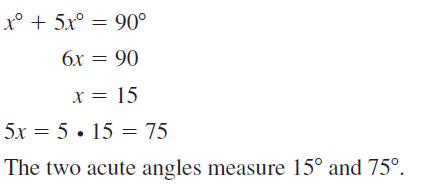
Question 24.
The measure of one acute angle is times the measure of the other acute angle.
Answer:
3x = x + 8
3x – x = 8
2x = 8
x = 8/2
x = 4
3x = 3(4) = 12
So, the measure of the second angle is also 12.
Question 25.
The measure of one acute angle is 3 times the sum of the measure of the other acute angle and 8.
Answer:
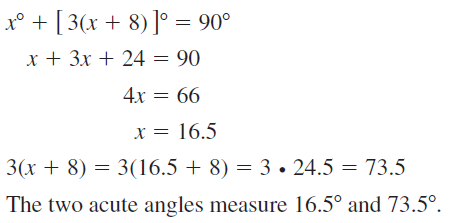
Question 26.
The measure of one acute angle is twice the difference of the measure of the other acute angle and 12.
Answer:
The measure of one acute angle is twice the difference of the measure of the other acute angle and 12.
x° + [2 (x – 12)]° = 90°
x° + 2x° – 2(12)° = 90°
3x° – 24° = 90°
3x° = 90° + 24°
3x° = 114°
x = 114° ÷ 3
x = 38°
So,
The 2 acute angle measures are: x°, 2 (x – 12)°
= 38°, 2 (38 – 12)°
= 38°, 2(26)°
= 38° , 52°
ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in finding m∠1.
Question 27.
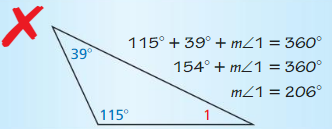
Answer:

Question 28.
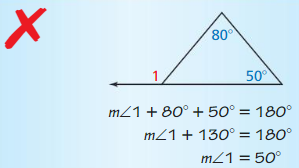
Answer:
The exterior angle of a triangle is equal to the sum of the non-adjacent interior angles of a triangle
The external angle is: ∠1
The interior angles are 80°, 50°
So,
∠1 = 80° + 50°
∠1 = 130°
Now,
The interior angle measure of ∠1= 180° – (External angle measure of 130°)
= 180° – 130°
= 50°
In Exercises 29-36, find the measure of the numbered angle.
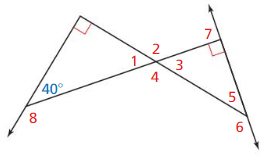
Question 29.
∠1
Answer:
![]()
Question 30.
∠2
Answer:
The external angle measure is equal to the sum of the non-adjacent interior angles
∠2 = 90° + 40°
∠2 = 130°
Question 31.
∠3
Answer:
![]()
Question 32.
∠3
Answer:
∠2 = ∠4
We can conclude that
∠2 = ∠4 = 130°
Question 33.
∠5
Answer:
![]()
Question 34.
∠6
Answer:
The external angle measure is equal to the sum of the non-adjacent interior angles
∠6 = 90° + ∠3
∠6 = 90° + 50°
∠6 = 140°
Question 35.
∠7
Answer:
![]()
Question 36.
∠8
Answer:
∠8 = 90° + ∠1
∠6 = 90° + 50°
∠6 = 140°
Question 37.
USING TOOLS
Three people are standing on a stage. The distances between the three people are shown in the diagram. Classify the triangle by its sides and by measuring its angles.
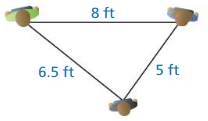
Answer:

Question 38.
USING STRUCTURE
Which of the following sets of angle measures could form a triangle? Select all that apply.
(A) 100°, 50°, 40°
Answer:
The given angles are: 100°, 50°, 40°
The sum of the angles of a triangle should be equal to 180°
The sum of the given angles = 100° + 50° + 40°
= 100° + 90°
= 190°
We can conclude that the given angles do not form a triangle
(B) 96°, 74°, 10°
Answer:
The sum of the given angles = 96° + 74° + 10°
= 96° + 84°
= 180°
Hence, the given angles forms a triangle
(C) 165°, 113°, 82°
Answer:
The sum of the angles of a triangle should be equal to 180°
The sum of the given angles = 165° + 113° + 82°
= 165° + 195°
= 360°
The sum of the exterior angles of a triangle is: 360°
We can conclude that the given angles form a triangle
(D) 101°, 41°, 38°
Answer:
The sum of the angles of a triangle should be equal to 180°
The sum of the given angles = 101° + 38° + 41°
= 101° + 79°
= 180°
We can conclude that the given angles forms a triangle
(E) 90°, 45°, 45°
Answer:
The sum of the given angles = 90° + 45° + 45°
= 90° + 90°
= 180°
We can conclude that the given angles forms a triangle
(F) 84°, 62°, 34°
Answer:
The sum of the angles of a triangle should be equal to 180°
The sum of the given angles = 84° + 62° + 34°
= 84° + 96°
= 180°
We can conclude that the given angles forms a triangle
Question 39.
MODELING WITH MATHEMATICS
You are bending a strip of metal into an isosceles triangle for a sculpture. The strip of metal is 20 inches long. The first bend is made 6 inches from one end. Describe two ways you could complete the triangle.
Answer:

Question 40.
THOUGHT-PROVOKING
Find and draw an object (or part of an object) that can be modeled by a triangle and an exterior angle. Describe the relationship between the interior angles of the triangle and the exterior angle in terms of the object.
Answer:
The sum of the interior angles of a given triangle is 180°
The sum of the exterior angles of a given triangle is 360°
The exterior angle measure = Sum of the two non-adjacent interior angles
Question 41.
PROVING A COROLLARY
Prove the Corollary to the Triangle Sum Theorem (Corollary 5. 1).
Given ∆ABC is a right triangle
Prove ∠A and ∠B are complementary
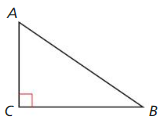
Answer:

Question 42.
PROVING A THEOREM
Prove the Exterior Angle Theorem (Theorem 5.2).
Given ∆ABC, exterior ∠ACD
Prove m∠A + m∠B = m∠ACD
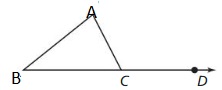
Answer:
It is given that
In ΔABC, the exterior angle is ∠ACD
We have to prove that
m∠A + m∠B = m∠ACD
Proof:
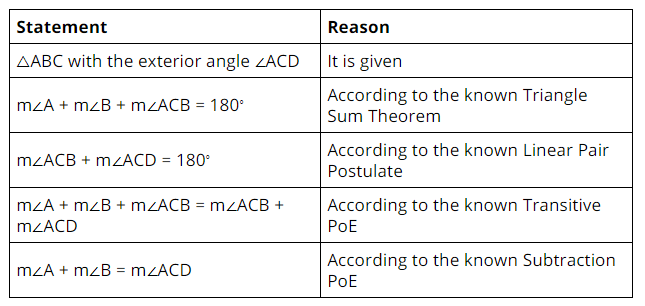
Hence, from the above,
We can conclude that
m∠A + m∠B = m∠ACD is proven
Question 43.
CRITICAL THINKING
Is it possible to draw an obtuse isosceles triangle? obtuse equilateral triangle? If so, provide examples. If not, explain why it is not possible.
Answer:

Question 44.
CRITICAL THINKING
Is it possible to draw a right isosceles triangle? right equilateral triangle? If so, provide an example. If not, explain why it is not possible.
Answer:
It is possible to draw a right isosceles triangle but it is not possible to draw a right equilateral triangle
We can observe that it is possible to draw right isosceles triangle but it is not possible to dran a right equilateral triangle
Question 45.
MATHEMATICAL CONNECTIONS
∆ABC is isosceles.
AB = x, and BC = 2x – 4.
a. Find two possible values for x when the perimeter of ∆ABC is 32.
b. How many possible values are there for x when the perimeter of ∆ABC is 12?
Answer:

Question 46.
HOW DO YOU SEE IT?
Classify the triangles, in as many ways as possible. without finding any measurements.
a. 
Answer:
We can observe that all the lengths of the sides of the triangle are equal
A triangle that has the length of all the sides equal is called an “Equilateral triangle”
We can conclude that the given triangle is an “Equilateral triangle”
b. 
Answer:
We can observe that the lengths of all the 3 sides are different
The triangle that has all the different side lengths is called a “Scalene triangle”
We can conclude that the given triangle is called a “Scalene triangle”
c. 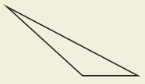
Answer:
We can observe that the length of all the 3 sides are different and 1 angle is obtuse i.e., greater than 90°
The triangle that has any angle obtuse is called an “Obtuse angled triangle”
We can conclude that the given triangle is an “Obtuse angled scalene triangle”
d. 
Answer:
We can observe that 1 angle is 90° and the 2 sides are perpendicular to each other
A triangle that has an angle of 90° and a slope -1 is called a “Right-angled triangle”
We can conclude that the given triangle is called a “Right-angled triangle”
Question 47.
ANALYZING RELATIONSHIPS
Which of the following could represent the measures of an exterior angle and two interior angles of a triangle? Select all that apply.
A) 100°, 62°, 38°
(B) 81°, 57°, 24°
(C) 119°, 68°, 49°
(D) 95°, 85°, 28°
(E) 92°, 78°, 68°
(F) 149°, 101°, 48°
Answer:

Question 48.
MAKING AN ARGUMENT
Your friend claims the measure of an exterior angle will always be greater than the sum of the nonadjacent interior angle measures. Is your friend correct? Explain your reasoning.
Answer:
According to the exterior angle theorem,
The external angle measure is always equal to the sum of the non-adjacent internal angle measures
But,
According to your friend,
The external angle measure will always be greater than the sum of the non-adjacent interior angle measures
We can conclude that your friend is not correct
MATHEMATICAL CONNECTIONS
In Exercises 49-52, find the values of x and y.
Question 49.
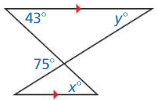
Answer:

Question 50.
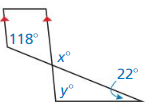
Answer:
By using the alternate angles theorem,
x = 118°
By using the exterior angle theorem,
x = y + 22°
y = x – 22°
y = 118° – 22°
y = 96°
Question 51.
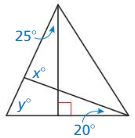
Answer:

Question 52.
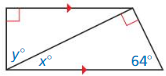
Answer:
By using the sum of interior angle measures,
x° + 64° + 90° = 180°
x° + 154° = 180°
x° = 180° – 154°
x° = 26°
Now,
By using the exterior angle theorem,
y° = x° + 64°
y° = 26° + 64°
y° = 90°
Question 53.
PROVING A THEOREM
Use the diagram to write a proof of the Triangle Sum Theorem (Theorem 5. 1). Your proof should be different from the proof of the Triangle Sum Theorem shown in this lesson.
Answer:


Maintaining Mathematical Proficiency
Use the diagram to find the measure of the segment or angle.
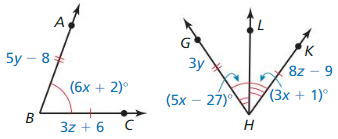
Question 54.
m∠KHL
Answer:
∠ABC = ∠GHK
∠KHL = ∠GHK / 2
So,
(6x + 2)° = (3x + 1)° + (5x – 27)°
6x – 3x – 5x = 1 – 27 – 2
6x – 8x = -27 – 1
-2x = -28
2x = 28
x = 28 ÷ 2
x = 14
So,
∠KHL = ∠GHK / 2
= [(3 (14) + 1)° + (5 (14) – 27)°] / 2
= [43° + 43°] / 2
= 86° / 2
= 43°
∠KHL = 43°
Question 55.
m∠ABC
Answer:
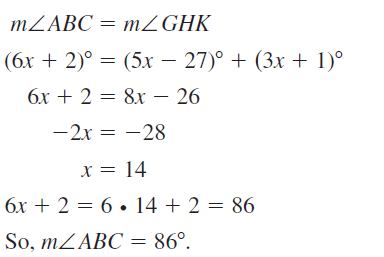
Question 56.
GH
Answer:
AB = GH
So,
3y = 5y – 8
3y – 5y = -8
-2y = -8
2y = 8
y = 8 ÷ 2
y = 4
So,
The value of GH = 3y = 3 (4) = 12
Question 57.
BC
Answer:
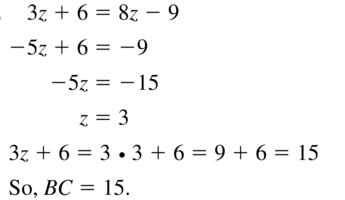
5.2 Congruent Polygons
Exploration 1
Describing Rigid Motions
Work with a partner: of the four transformations you studied in Chapter 4, which are rigid motions? Under a rigid motion. why is the image of a triangle always congruent to the original triangle? Explain your reasoning.

Answer:
Rigid motion occurs in geometry when an object moves but maintains its shape and size, which is unlike non-rigid motions, such as dilation, in which the object’s size changes. All rigid motion starts with the original object, called the pre-image, and results in the transformed object, called the image.
There are 4 types of rigid motion.
a. Translation
b. Rotation
c. Reflection
d. Glide reflection
We know that,
Rotation only occurs in terms of 90° or 180°
Now,
The given transformations are:

The first figure and the second figure are different
The second figure and the third figure are the same in shape
The first figure and the fourth figure are the same in shape
We can say that the first and the fourth figures are rigid motions
W can say that the second and the third figures are rigid motions
In the second and the third figures,
The “Rotation” takes place i.e., the second figure is rotated 180° keeping the original shape
In the first and the fourth figures,
The “Reflection” takes place i.e., the first figure is reflected keeping the original shape
The image of the triangle is always congruent to the original triangle because of the “Translation” i.e., the original triangle and the image of the triangle have the same sides and the same angles but not in the same position.
Exploration 2
Finding a Composition of Rigid Motions
Work with a partner. Describe a composition of rigid motions that maps ∆ABC to ∆DEF. Use dynamic geometry software to verify your answer.
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
a. ∆ABC ≅ ∆DEF
Answer:
b. ∆ABC ≅ ∆DEF
Answer:
c. ∆ABC ≅ ∆DEF
Answer:
d. ∆ABC ≅ ∆DEF
Answer:
Communicate Your Answer
Question 3.
Given two congruent triangles. how can you use rigid motions to map one triangle to the other triangle?
Answer:
Let the one triangle be the original or pre-image triangle and another triangle be the image triangle.
We can use rigid motions on the original triangle to create the image triangle as the rigid motions won’t alter the size and shape of the figure and it maps each part of the triangle with the corresponding part of its image.
Question 4.
The vertices of ∆ABC are A(1, 1), B(3, 2), and C(4, 4). The vertices of ∆DEF are D(2, – 1), E(0, 0), and F(- 1, 2). Describe a composition of rigid motions that maps ∆ABC to ∆DEF.
Answer:
Lesson 5.2 Congruent Polygons
Monitoring Progress
In the diagram, ABGH ≅ CDEF.
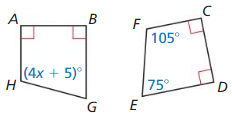
Question 1.
Identify all pairs of congruent corresponding parts.
Answer:
∠A = ∠C, ∠B = ∠D, ∠H = ∠F, ∠G = ∠E
AB = CD, BG= DE, HG = ED, AH = CF
Question 2.
Find the value of x.
Answer:
∠H = ∠F
(4x + 5) = 105
4x = 100
x = 25
Question 3.
In the diagram at the left. show that ∆PTS ≅ ∆RTQ.
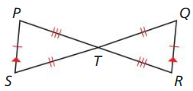
Answer:
PS = QR, ST = TQ, PT = TR
∆PTS ≅ ∆RTQ
Use the diagram.
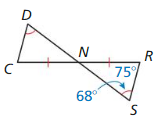
Question 4.
Find m∠DCN.
Answer:
∆CDN ≅ SRN
So, m∠DCN = m∠SRN
m∠DCN = 75°
Question 5.
What additional information is needed to conclude that ∆NDC ≅ ∆NSR?
Answer:
The sides RC = RS, DN = NS and m∠DNC = m∠RNS
Exercise 5.2 Congruent Polygons
Question 1.
WRITING
Based on this lesson. what information do you need to prove that two triangles are congruent? Explain your reasoning.
Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
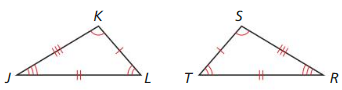
Is ∆JKL ≅ ∆RST?
Is ∆KJL ≅ ∆SRT?
Is ∆JLK ≅ ∆STR?
Is ∆LKJ ≅ ∆TSR?
Answer:
∆JLK ≅ ∆STR is different
Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4. identify all pairs of congruent corresponding parts. Then write another congruence statement for the polygons.
Question 3.
∆ABC ≅ ∆DEF
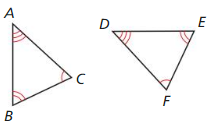
Answer:
Question 4.
GHJK ≅ QRST
Answer:
Corresponding angles: ∠G = ∠Q, ∠H = ∠R, ∠K = ∠T, ∠J = ∠T
Correspoding sides: ST = JK, TQ = KG, QR = GH, RS = HJ
Thus, GHJK ≅ QRST
In Exercises 5-8, ∆XYZ ≅ ∆MNL. Copy and complete the statement.

Question 5.
m∠Y = ______
Answer:
![]()
Question 6.
m∠M = ______
Answer:
m∠M = m∠X, so m∠M = 33°
Question 7.
m∠Z = _______
Answer:

Question 8.
XY= _______
Answer:
XY = MN, so, XY = 8
In Exercises 9 and 10. find the values of x and y.
Question 9.
ABCD ≅ EFGH
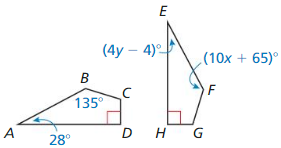
Answer:
Question 10.
∆MNP ≅ ∆TUS
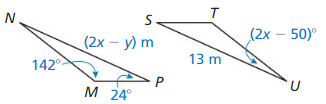
Answer:
Sum of angles = 180°
142 + 24 + 2x – 50 = 180
116 + 2x = 180
2x = 64
x = 32°
NP = TU
2x – y = 13
2(32) – y = 13
64 – 13 = y
y = 51°
In Exercises 11 and 12. show that the polygons are congruent. Explain your reasoning.
Question 11.
Answer:
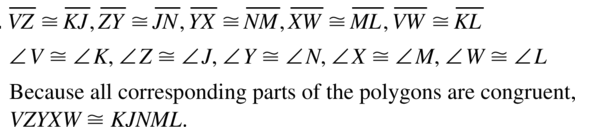
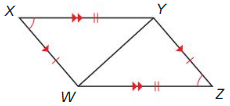
Question 12.
Answer:
∠X = ∠Z, ∠XWY = ∠ZWY, ∠XYW = ∠ZWY
WX = YZ, XY = WZ
All corresponding parts of polygons are congruent
△ XWZ ≅ △ ZWY
In Exercises 13 and 14, find m∠1.
Question 13.
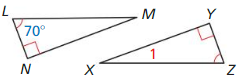
Answer:
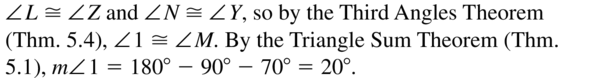
Question 14.
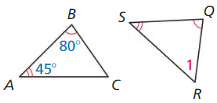
Answer:
∠1 = 180 – (80 + 45) = 180 – 125
∠1 = 55°
Question 15.
PROOF
Triangular postage stamps, like the ones shown, are highly valued by stamp collectors. Prove that ∆AEB ≅ ∆CED.
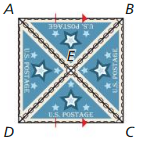
Given \(\overline{A B}\) || \(\overline{D C}\), \(\overline{A B}\) ≅ \(\overline{D C}\) is the midpoint of \(\overline{A C}\) and \(\overline{B D}\)
Prove ∆AEB ≅ ∆CED
Answer:

Question 16.
PROOF
Use the information in the figure to prove that ∆ABG ≅ ∆DCF
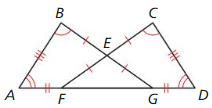
Answer:
FE = EG, BE = EC, AF = GD, AB = CD
∠B = ∠C, ∠A = ∠D
All the corresponding pairs are similar
So, ∆ABG ≅ ∆DCF
ERROR ANALYSIS
In Exercises 17 and 18, describe and correct the error.
Question 17.
Answer:

Question 18.
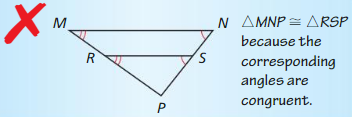
Answer:
∠N = ∠S, ∠M = ∠R, MN ≠ RS
The corresponding sides are not congruent.
So, ∆MNP is not similar to ∆RSP
Question 19.
PROVING A THEOREM
Prove the Third Angles Theorem (Theorem 5.4) by using the Triangle Sum Theorem (Theorem 5. 1).
Answer:


Question 20.
THOUGHT PROVOKING
Draw a triangle. Copy the triangle multiple times to create a rug design made of congruent triangles. Which property guarantees that all the triangles are congruent?
Answer:
The interior angles of these triangles are equal because one pair of angles is equal because they are cross angles and the other pairs are equal because the angles are on the transversal.
When the angles are equal, then the sides of these triangles are also equal that means these triangles are congruent.
Question 21.
REASONING
∆JKL is congruent to ∆XYZ Identify all pairs of congruent corresponding parts.
Answer:
Question 22.
HOW DO YOU SEE IT?
In the diagram, ABEF ≅ CDEF
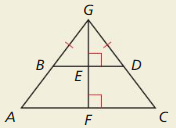
a. Explain how you know that \(\overline{B E}\) ≅ \(\overline{D E}\) and ∠ABE ≅∠CDE.
Answer:
ABEF ≅ CDEF
So by using the property of corresponding parts of congruent triangles
\(\overline{B E}\) ≅ \(\overline{D E}\) are corresponding parts of congruent triangles
∠ABE ≅∠CDE are congruent
b. Explain how you know that ∠GBE ≅ ∠GDE.
Answer:
GF is the altitude of triangle AGC.
∠GED = 90 so, ∠GEB = 90
∠GBE ≅ ∠GDE
c. Explain how you know that ∠GEB ≅ ∠GED.
Answer:
GF is the altitude of triangle AGC. So, ∠GEB ≅ ∠GED
d. Do you have enough information to prove that ∠BEG ≅ ∠DEG? Explain.
Answer:
\(\overline{B E}\) ≅ \(\overline{D E}\)
∠GBE ≅ ∠GDE
∠GEB ≅ ∠GED
So, by ASA congruency of triangle
ΔBEG ≅ ΔDEG
MATHEMATICAL CONNECTIONS
In Exercises 23 and 24, use the given information to write and solve a system of linear equations to find the values of x and y.
Question 23.
∆LMN ≅ ∆PQR. m∠L = 40°, m∠M = 90° m∠P = (17x – y)°. m∠R (2x + 4y)°
Answer:

Question 24.
∆STU ≅ ∆XYZ, m∠T = 28°, m∠U = (4x + y)°, m∠X = 130°, m∠Y = (8x – 6y)°
Answer:
m∠Y = m∠T
28 = (8x – 6y)°
4x – 3y = 14 —- (I)
m∠T + m∠S + m∠U = 180°
28°+ 130° + (4x + y)° = 180°
158 + 4x + y = 180
4x + y = 22 —- ( II)
4x – 3y – 4x – y = 14 – 22
-4y = -8
y = 2
Put y = 2 in (II)
4x + 2 = 22
4x = 20
x = 5
Question 25.
PROOF
Prove that the criteria for congruent triangles in this lesson is equivalent to the definition of congruence in terms of rigid motions.
Answer:

Maintaining Mathematical Proficiency
What can you conclude from the diagram?
Question 26.
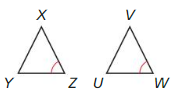
Answer:
∠Z = ∠W
Question 27.
Answer:
![]()
Question 28.
Answer:
JK = KM
∠J = ∠M
Question 29.
Answer:
![]()
5.3 Proving Triangle Congruence by SAS
Exploration 1
Drawing Triangles
Work with a partner.
Use dynamic geometry software.
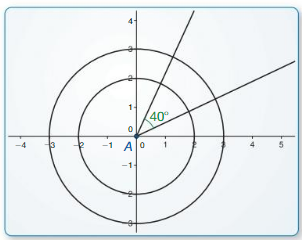
a. Construct circles with radii of 2 units and 3 units centered at the origin. Construct a 40° angle with its vertex at the origin. Label the vertex A.
Answer:
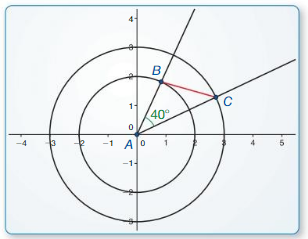
b. Locate the point where one ray of the angle intersects the smaller circle and label this point B. Locate the point where the other ray of the angle intersects the larger circle and label this point C. Then draw ∆ABC.
Answer:
c. Find BC, m∠B, and m∠C.
Answer:
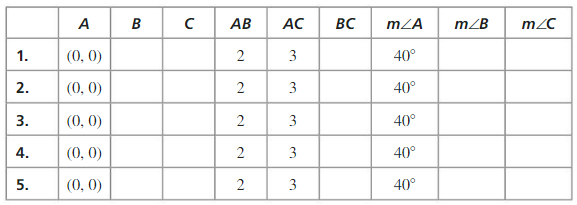
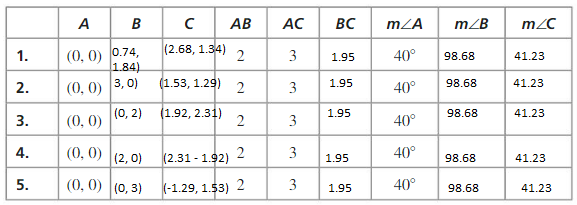
d. Repeat parts (a)-(c) several times. redrawing the angle indifferent positions. Keep track of your results by copying and completing the table below. What can you conclude?
USING TOOLS STRATEGICALLY
To be proficient in math, you need to use technology to help visualize the results of varying assumptions, explore consequences, and compare predictions with data.
Answer:
Communicate Your Answer
Question 2.
What can you conclude about two triangles when you know that two pairs of corresponding sides and the corresponding included angles are congruent?
Answer:
If two pairs of corresponding angles in a pair of triangles are congruent, then the triangles are said to be similar. If two angle pairs are the same, then the third pair must also be equal. When the three angle pairs are all equal, the three pairs of sides must also be in proportion.
Question 3.
How would you prove your conclusion in Exploration 1(d)?
Answer:
Lesson 5.3 Proving Triangle Congruence by SAS
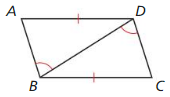
Monitoring Progress
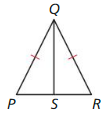
In the diagram, ABCD is a square with four congruent sides and four right
angles. R, S, T, and U are the midpoints of the sides of ABCD. Also, \(\overline{R T}\) ⊥ \(\overline{S U}\) and \(\overline{S V}\) ≅ \(\overline{V U}\).
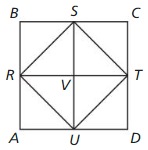
Question 1.
Prove that ∆SVR ≅ ∆UVR.
Answer:
ABCD is a square with four congruent sides and four right angles. R, S, T, and U are the midpoints of the sides of ABCD.
So, SV = VU, RS = RU, ∠S = ∠U
All the corresponding sides and angles are congruent.
∆SVR ≅ ∆UVR
Question 2.
Prove that ∆BSR ≅ ∆DUT.
Answer:
∠B = ∠D, ∠S = ∠U, ∠R = ∠T and BS = UD, BR = TD, SR = TU
So, ∆BSR ≅ ∆DUT
Question 3.
You are designing the window shown in the photo. You want to make ∆DRA congruent to ∆DRG. You design the window so that \(\overline{D A}\) ≅ \(\overline{D G}\) and ∠ADR ≅ ∠GDR. Use the SAS Congruence Theorem to prove ∆DRA ≅ ∆DRG.
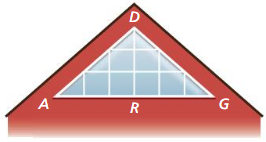
Answer:
When you rotate ∆DRG 90° towards left, then ∆DRG coincides ∆DRA.
According to the Side Angle Side Congruence theorem, ∆DRA ≅ ∆DRG
Exercise 5.3 Proving Triangle Congruence by SAS
vocabulary and core concept check
Question 1.
WRITING
What is an included angle?
Answer:
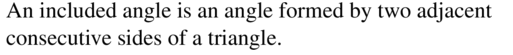
Question 2.
COMPLETE THE SENTENCE
If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then __________ .
Answer:
If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then two triangles are congruent according to the SAS Congruence Theorem.
Monitoring progress and Modeling with Mathematics
In Exercises 3-8, name the included an1e between the pair of sides given.
Question 3.
\(\overline{J K}\) and \(\overline{K L}\)
Answer:
![]()
Question 4.
\(\overline{P K}\) and \(\overline{L K}\)
Answer:
∠KLP is the included angle between \(\overline{P K}\) and \(\overline{L K}\)
Question 5.
\(\overline{L P}\) and \(\overline{L K}\)
Answer:
![]()
Question 6.
\(\overline{J L}\) and \(\overline{J K}\)
Answer:
∠KJL is the included angle between \(\overline{J L}\) and \(\overline{J K}\)
Question 7.
\(\overline{K L}\) and \(\overline{J L}\)
Answer:
![]()
Question 8.
\(\overline{K P}\) and \(\overline{P L}\)
Answer:
∠KPL is the included angle between \(\overline{K P}\) and \(\overline{P L}\)
In Exercises 9-14, decide whether enough information is given to prove that the triangles are congruent using the SAS Congruence Theorem (Theorem 5.5). Explain.
Question 9.
∆ABD, ∆CDB
Answer:
![]()
Question 10.
∆LMN, ∆NQP
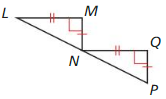
Answer:
Yes, two pairs of sides and the included angles are congruent.
Question 11.
∆YXZ, ∆WXZ
Answer:
![]()
Question 12.
∆QRV, ∆TSU
Answer:
Yes, two pairs of sides and the included angles are congruent.
Question 13.
∆EFH, ∆GHF
Answer:
![]()
Question 14.
∆KLM, ∆MNK
Answer:
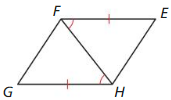
No, one of the congruent angles is not the included angle.
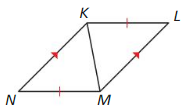
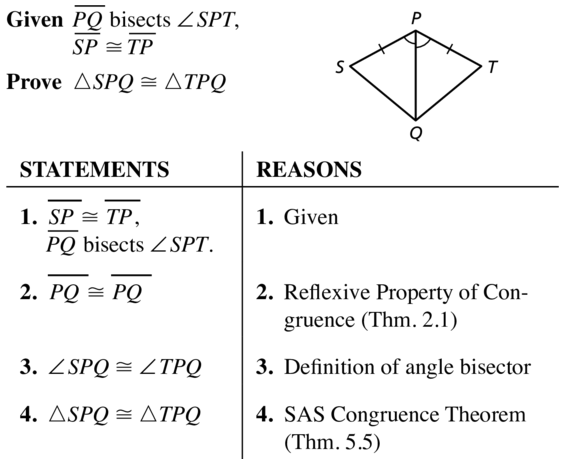
In Exercises 15 – 18, write a proof.
Question 15.
Given \(\overline{P Q}\) bisects ∠SPT, \(\overline{S P}\) ≅ \(\overline{T P}\)
Prove ∆SPQ ≅ ∆TPQ
Answer:
Question 16.
Given \(\overline{A B}\) ≅ \(\overline{C D}\), \(\overline{A B}\) || \(\overline{C D}\)
Prove ∆ABC ≅ ∆CDA
Answer:
AB || CD
∠BAC = ∠ACD (Alternative Interior Angle)
∠DAC = ∠BCA (Alternative Interior Angle)
AC = AC (Reflexive property of congruence)
∆ABC ≅ ∆CDA by Angle Side Angle Congruence Theorem.
Question 17.
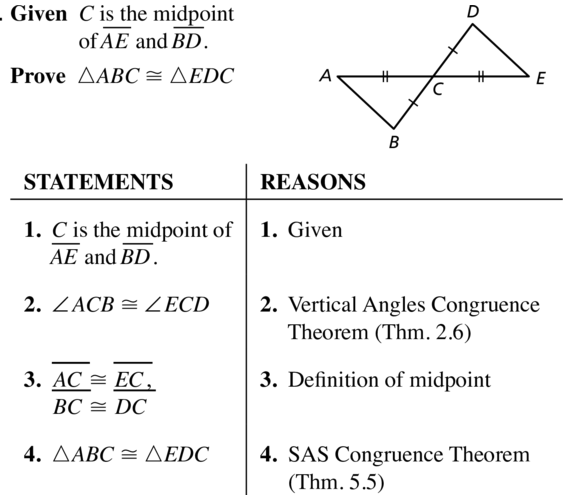
Given C is the midpoint of \(\overline{A E}\) and \(\overline{B D}\)
Prove ∆ABC ≅ ∆EDC
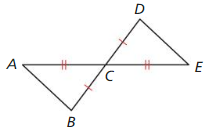
Answer:
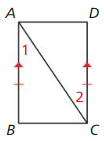
Question 18.
Given \(\overline{P T}\) ≅ \(\overline{R T}\), \(\overline{Q T}\) ≅ \(\overline{S T}\)
Prove ∆PQT ≅ ∆RST
Answer:
\(\overline{P T}\) ≅ \(\overline{R T}\)
\(\overline{Q T}\) ≅ \(\overline{S T}\)
In a parallelogram, diagonals bisect at 90 degrees.
∠PTQ = ∠STR (Vertical Angles Congruence Theorem)
∆PQT ≅ ∆RST (SAS Congruence Theorem)
In Exercises 19-22, use the given information to name two triangles that are congruent. Explain your reasoning.
Question 19.
∠SRT ≅ ∠URT, and R is the center of the circle.
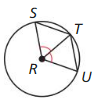
Answer:

Question 20.
ABCD is a square with four congruent sides and four congruent angles.
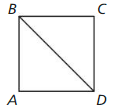
Answer:
BC ≅ AD, AB ≅ CD as four sides are congruent
BD ≅ BD by the reflexive property of congruence.
∠A = ∠C, ∠DBA = ∠CBD
All the corresponding sides and angles are congruent
△BAD ≅ △BCD
Question 21.
RSTUV is a regular pentagon.
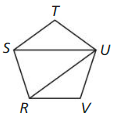
Answer:

Question 22.
\(\overline{M K}\) ⊥ \(\overline{M N}\), \(\overline{K L}\) ⊥ \(\overline{N L}\), and M and L are centers of circles.
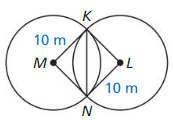
Answer:
∠M = ∠L = 90°
MK = LN
NK = NK by the reflexive property of congruence
△ MKN ≅ △LKN
CONSTRUCTION
In Exercises 23 and 24, construct a triangle that is congruent to ∆ABC using the SAS Congruence Theorem (Theorem 5.5).
Question 23.
Answer:
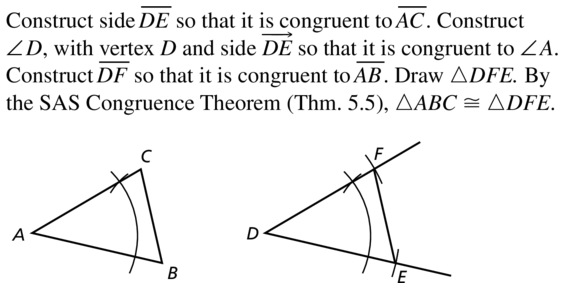
Question 24.
Answer:
Construct side DE which is congruent to AC. Construct ∠D with vertex D and side DE so that it is congruent to ∠A.
Construct DF that is congruent to AB. Draw △DFE. By SAS congruence theorem △ABC ≅ △DFE
Question 25.
ERROR ANALYSIS
Describe and correct the error in finding the value of x.
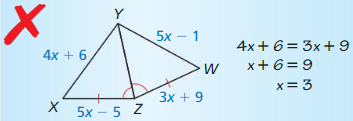
Answer:

Question 26.
HOW DO YOU SEE IT?
What additional information do you need to prove that ∆ABC ≅ ∆DBC?
Answer:
One included congruent angle is needed to prove that ∆ABC ≅ ∆DBC.
Question 27.
PROOF
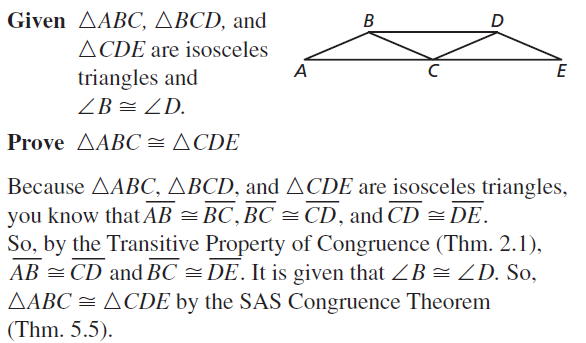
The Navajo rug is made of isosceles triangles. You know ∠B ≅∠D. Use the SAS Congruence Theorem (Theorem 5.5 to show that ∆ABC ≅ ∆CDE. (See Example 3.)
Answer:
Question 28.
THOUGHT PROVOKING
There are six possible subsets of three sides or angles of a triangle: SSS, SAS, SSA, AAA, ASA, and AAS. Which of these correspond to congruence theorems? For those that do not, give a counterexample.
Answer:
SSS, SAS, ASA and AAS are congruence theorems.
SSA does not prove two traingles congruent. For example, two triangles have the same angle and two common sides, but they are not congruent.
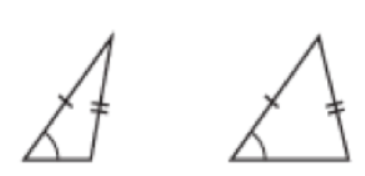
AAA does not prove two triangles congruent. For example, these two triangles have the same angles but are not similar.
Question 29.
MATHEMATICAL CONNECTIONS
Prove that
∆ABC ≅ ∆DEC
Then find the values of x and y.
Answer:

Question 30.
MAKING AN ARGUMENT
Your friend claims it is possible to Construct a triangle congruent to ∆ABC by first constructing \(\overline{A B}\) and \(\overline{A C}\), and then copying ∠C. Is your friend correct? Explain your reasoning.
Answer:
My friend is wrong. Because to copy the ∠C, you need to construct the vertex C first. But by constructing \(\overline{A B}\) and \(\overline{A C}\), you will get vertex A.
Question 31.
PROVING A THEOREM
Prove the Reflections in Intersecting Lines Theorem (Theorem 4.3).
Answer:



Maintaining Mathematical Proficiency
Classify the triangle by its sides and by measuring its angles.
Question 32.
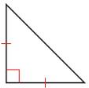
Answer:
Two sides are equal and one angle is the right angle.
The triangle is right angles isosceles triangle
Question 33.
Answer:
Question 34.
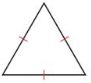
Answer:
Three sides of the triangle are equal. It is an equilateral triangle.
Question 35.
Answer:

5.4 Equilateral and Isosceles Triangles
Exploration 1
Writing a Conjecture about Isosceles Triangles
Work with a partner: Use dynamic geometry software.
a. Construct a circle with a radius of 3 units centered at the origin.
Answer:
b. Construct ∆ABC so that B and C are on the circle and A is at the origin.
Answer:
c. Recall that a triangle is isosceles if it has at least two congruent sides. Explain why ∆ABC is an isosceles triangle.
Answer:
d. What do you observe about the angles of ∆ABC?
Answer:
e. Repeat parts (a)-(d) with several other isosceles triangles using circles of different radii. Keep track of your observations by copying and completing the table below. Then write a conjecture about the angle measures of an isosceles triangle.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures.
Answer:
f. Write the converse of the conjecture you wrote in part (e). Is the converse true?
Answer:
Communicate Your Answer
Question 2.
What conjectures can you make about the side lengths and angle measures of an
isosceles triangle?
Answer:
Question 3.
How would you prove your conclusion in Exploration 1 (e)? in Exploration 1(f)?
Answer:
The conjectures obtained in 1 (e) and 1 (f) have been proved successfully by constructing an isosceles triangle with two congruent sides for the first conjecture, and then constructing another isosceles triangle with two congruent base angles.
The above figure shows the first conjecture for an isosceles triangle.
The above figure, shows the second conjecture for an isosceles triangle.
Lesson 5.4 Equilateral and Isosceles Triangles
Monitoring Progress
Copy and complete the statement.
Question 1.
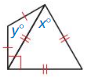
If \(\overline{H G}\) ≅ \(\overline{H K}\), then ∠ _______ ≅ ∠ _______ .
Answer:
∠G = ∠K by using the base angles theorem.
Question 2.
If ∠KHJ ≅∠KJH, then ______ ≅ ______ .
Answer:
\(\overline{K H}\) ≅ \(\overline{K J}\)
Question 3.
Find the length of \(\overline{S T}\) of the triangle at the left.
Answer:
As per Collary to the Converse of the Base Angles Theorem, ST = SU = TU
\(\overline{S T}\) = 5
Question 4.
Find the value of x and y in the diagram.
Answer:
As all sides are equal, angles are also equal.
So, x° = 60°
y° = 90° – 60° = 30°
Question 5.
In Example 4, show that ∆PTS ≅ ∆QTR
Answer:
TS ≅ TR,
PS ≅ QR
∠TPS = ∠TQR
∆PTS ≅ ∆QTR by SAS theorem.
Exercise 5.4 Equilateral and Isosceles Triangles
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Describe how to identify the vertex angle of an isosceles triangle.
Answer:
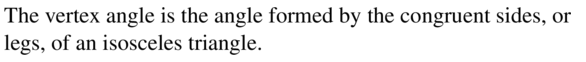
Question 2.
WRITING
What is the relationship between the base angles of an isosceles triangle? Explain.
Answer:
An isosceles triangle consists of two equal legs and one base. There are two equal angles on the base. These are called base angles. So, the base angles are opposite to the congruent sides. Using the base angle theorem, we can conclude that the base angles of an isosceles triangle are congruent.
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6. copy and complete the statement. State which theorem you used.
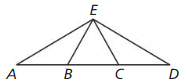
Question 3.
If \(\overline{A E}\) ≅ \(\overline{D E}\) then ∠_____ ≅ ∠_____ .
Answer:
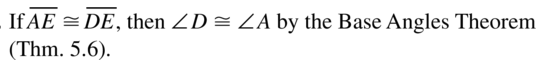
Question 4.
If \(\overline{A B}\) ≅ \(\overline{E B}\) then ∠_____ ≅ ∠_____ .
Answer:
If \(\overline{A B}\) ≅ \(\overline{E B}\) then ∠A ≅ ∠E by the Base Angles Theorem.
Question 5.
If ∠D ≅ ∠CED, then _______ ≅ _______ .
Answer:
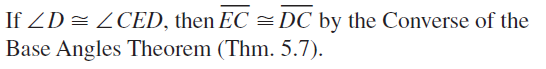
Question 6.
If ∠EBC ≅ ∠ECB, then _______ ≅ _______ .
Answer:
If ∠EBC ≅ ∠ECB, then EC ≅ EB by the converse of the base angles theorem.
In Exercises 7-10. find the value of x.
Question 7.
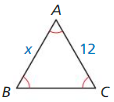
Answer:
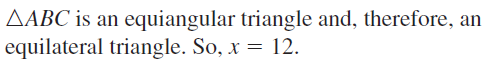
Question 8.
Answer:
As ∠L, ∠N are 60 degrees so ∠M is also 60 degrees
So, LM = LN = MN
x = 16
Question 9.
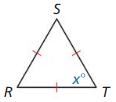
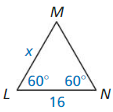
Answer:
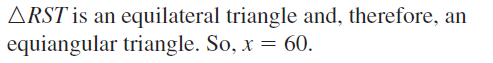
Question 10.
Answer:
All the sides are equal so angles are also equal
3x + 3x + 3x = 180
9x = 180
x = 20°
Question 11.
MODELING WITH MATHEMATICS
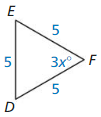
The dimensions of a sports pennant are given in the diagram. Find the values of x and y.

Answer:
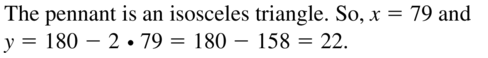
Question 12.
MODELING WITH MATHEMATICS
A logo in an advertisement is an equilateral triangle with a side length of 7 centimeters. Sketch the logo and give the measure of each side.
Answer:
An equilateral triangle has three sides of equal length. So, the remaining two sides are also 7 cm.
In Exercises 13-16, find the values of x and y.
Question 13.
Answer:

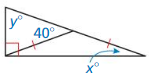
Question 14.
Answer:
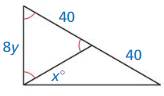
Question 15.
Answer:

Question 16.
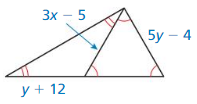
Answer:
3x – 5 = 5y – 4
3x – 5y + 4 = 0 —- (i)
y + 12 = 3x – 5
3x – y – 17 = 0 —- (ii)
Subtract (i) from (ii)
3x – y – 17 – 3x + 5y – 4 = 0
4y – 21 = 0
4y = 21
y = 5.25
Put y = 5.25 in (ii)
3x – 5.25 – 17 = 0
3x – 22.25 = 0
3x = 22.25
x = 7.416
CONSTRUCTION
In Exercises 17 and 18, construct an equilateral triangle whose sides are the given length.
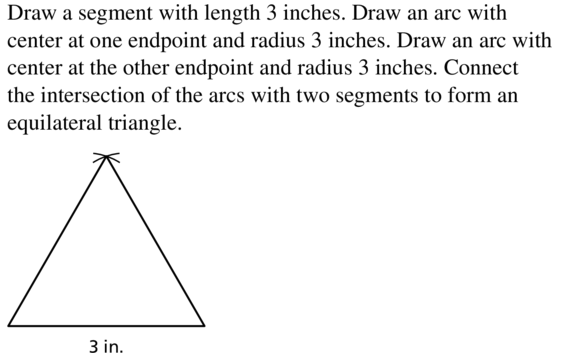
Question 17.
3 inches
Answer:
Question 18.
1.25 inches
Answer:
Construct the base leg with length 1.25 inches and draw an arc with center at one of the endpoints and a radius 1.25 in.
Draw another arc that intersects the first arc with the same radius and from another endpoint of the base leg.
Connect intersection of arcs to two endpoints of the base to form an equilateral triangle.
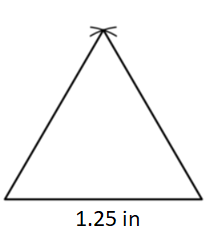
Question 19.
ERROR ANALYSIS
Describe and correct the error in finding the length of \(\overline{B C}\).
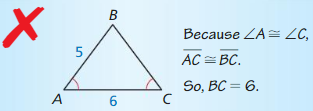
Answer:

Question 20.
PROBLEM SOLVING
The diagram represents part of the exterior of the Bow Tower in Calgary. Alberta, Canada, In the diagram. ∆ABD and ∆CBD arc congruent equilateral triangles.
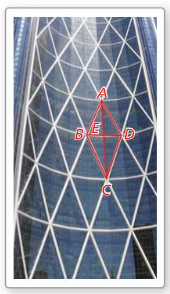
a. Explain why ∆ABC is isosceles.
Answer:
AB and BC have the same length.
∆ABC is isosceles.
b. Explain ∠BAE ≅ ∠BCE.
Answer:
AC is a diagonal that cuts the angles of the opposite vertex into two half. So, ∠BAE ≅ ∠BCE.
c. Show that ∆ABE and ∆CBE are congruent.
Answer:
AB ≅ BC, BE ≅ BE and ∠BAE ≅ ∠BCE
By SAS theorem, ∆ABE and ∆CBE are congruent.
d. Find the measure of ∠BAE.
Answer:
∠BAE ≅ ∠BCE.
Question 21.
FINDING A PATTERN
In the pattern shown. each small triangle is an equilateral triangle with an area of 1 square unit.
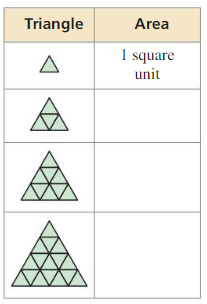
a. Explain how you know that an triangle made out of equilateral triangles is equilateral.
b. Find the areas of the first four triangles in the pattern.
c. Describe any patterns in the areas. Predict the area of the seventh triangle in the pattern. Explain your reasoning.
Answer:

Question 22.
REASONING
The base of isosceles ∆XYZ is \(\overline{Y Z}\). What
can you prove? Select all that apply.
(A) \(\overline{X Y}\) ≅ \(\overline{X Z}\)
(B) ∠X ≅ ∠Y
(C) ∠Y ≅ ∠Z
(D) \(\overline{Y Z}\) ≅ \(\overline{Z X}\)
Answer:
If, \(\overline{Y Z}\) is base of isosceles ∆XYZ.
Then, let us take \(\overline{X Y}\) ≅ \(\overline{X Z}\)
If \(\overline{X Y}\) ≅ \(\overline{X Z}\), then ∠Y ≅ ∠Z.
In Exercises 23 and 24, find the perimeter of the triangle.
Question 23.
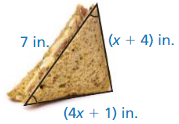
Answer:
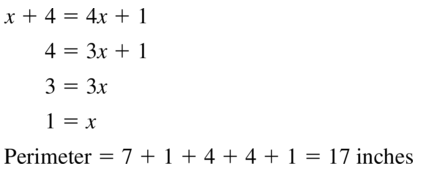
Question 24.
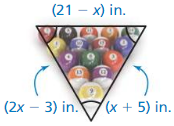
Answer:
21 – x = 2x – 3
21 + 3 = 2x + x
24 = 3x
x = 8
Perimeter = 13 + 13 + 13 = 39
MODELING WITH MATHEMATICS
In Exercises 25 – 28. use the diagram based on the color wheel. The 12 triangles in the diagram are isosceles triangles with congruent vertex angles.
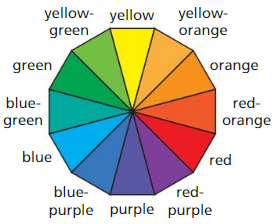
Question 25.
Complementary colors lie directly opposite each other on the color wheel. Explain how you know that the yellow triangle is congruent to the purple triangle.
Answer:

Question 26.
The measure of the vertex angle of the yellow triangle is 30°. Find the measures of the base angles.
Answer:
2x° + 30° = 180°
2x = 180 – 30 = 150°
x° = 75°
Question 27.
Trace the color wheel. Then form a triangle whose vertices are the midpoints of the bases of the red. yellow. and blue triangles. (These colors are the primary colors.) What type of triangle is this?
Answer:
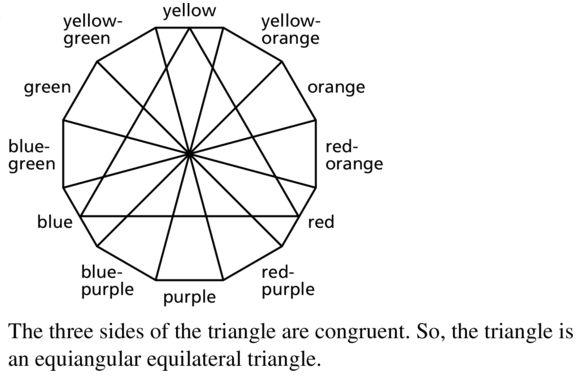
Question 28.
Other triangles can be brined on the color wheel that are congruent to the triangle in Exercise 27. The colors on the vertices of these triangles are called triads. What are the possible triads?
Answer:
Question 29.
CRITICAL THINKING
Are isosceles triangles always acute triangles? Explain your reasoning.
Answer:
Question 30.
CRITICAL THINKING
Is it possible for an equilateral triangle to have an angle measure other than 60°? Explain your reasoning.
Answer:
No, because an equilateral triangle has all the angles of equal measurement and the sum of angles in a triangle must be equal to 180°.
So, it is not possible for an angle measure other than 60° in an equilateral triangle.
Question 31.
MATHEMATICAL CONNECTIONS
The lengths of the sides of a triangle are 3t, 5t – 12, and t + 20. Find the values of t that make the triangle isosceles. Explain your reasoning.
Answer:
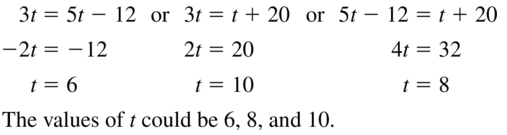
Question 32.
MATHEMATICAL CONNECTIONS
The measure of an exterior angle of an isosceles triangle is x°. Write expressions representing the possible angle measures of the triangle in terms of x.
Answer:
If x is the exterior angle of a triangle then the interior angle of the triangle that is supplementary with this angle is equal to 180° – x.
Exterior angle of a triangle is equal to the sum of 2 opposite interior angles on the triangle. Based on this, it can be said that the 2 other interior angles can be 0.25x and 0.75x
Question 33.
WRITING
Explain why the measure of the vertex angle of an isosceles triangle must be an even number of degrees when the measures of all the angles of the triangle are whole numbers.
Answer:
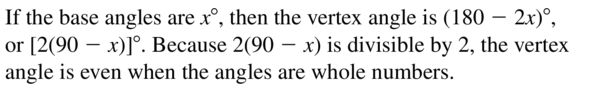
Question 34.
PROBLEM SOLVING
The triangular faces of the peaks on a roof arc congruent isosceles triangles with vertex angles U and V.
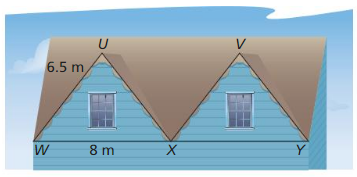
a. Name two angles congruent to ∠WUX. Explain your reasoning.
b. Find the distance between points U and V.
Answer:
a. ∠WUX ≅ ∠XVY
∠WUX ≅ ∠UXV
b. The distance between thee points U and V is 8 m.
Question 35.
PROBLEM SOLVING
A boat is traveling parallel to the shore along \(\vec{R}\)T. When the boat is at point R, the captain measures the angle to the lighthouse as 35°. After the boat has traveled 2.1 miles, the captain measures the angle to the lighthouse to be 70°.
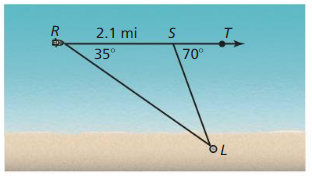
a. Find SL. Explain your reasoning.
b. Explain how to find the distance between the boat and the shoreline.
Answer:

Question 36.
THOUGHT PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry, do all equiangular triangles have the same angle measures? Justify your answer.
Answer:
Question 37.
PROVING A COROLLARY
Prove that the Corollary to the Base Angles Theorem (Corollary 5.2) follows from the Base Angles Theorem (Theorem 5.6).
Answer:

Question 38.
HOW DO YOU SEE IT?
You are designing fabric purses to sell at the school fair.
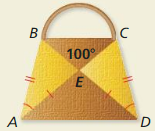
a. Explain why ∆ABE ≅ ∆DCE.
b. Name the isosceles triangles in the purse.
c. Name three angles that are congruent to ∠EAD.
Answer:
a. AB ≅ CD, AE ≅ ED and ∠A ≅ ∠D
So, ∆ABE ≅ ∆DCE by SAS theorem.
b. ∠EAD ≅ ∠AED ≅ ∠EDA
Question 39.
PROVING A COROLLARY
Prove that the Corollary to the Converse of the Base Angles Theorem (Corollary 5.3) follows from the Converse of the Base Angles Theorem (Theorem 5.7)
Answer:

Question 40.
MAKING AN ARGUMENT
The coordinates of two points are T(0, 6) and U(6, 0) Your friend claims that points T, U, and V will always be the vertices of an isosceles triangle when V is any point on the line y = x. Is your friend correct? Explain your reasoning.
Answer:
We know that the coordinates of two points are T(0, 6) and U (6, 0)
We also consider that V is any point on the line y = x
The coordinates of V be x = 3, y = 3. So V(3, 3)
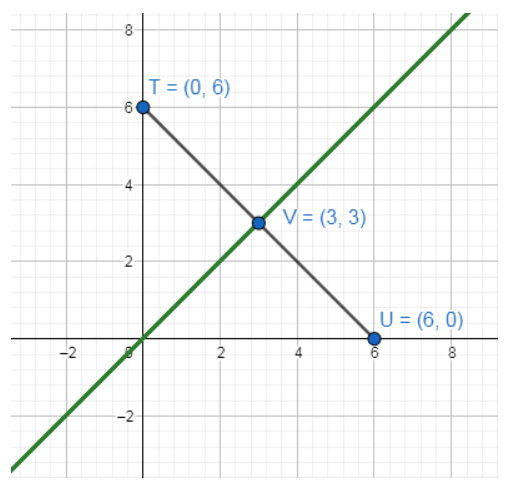
When we connect the points T, V, U we can see that we have not obtained an isosceles triangle.
Question 41.
PROOF
Use the diagram to prove that ∆DEF is equilateral.
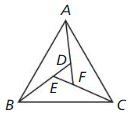
Given ∆ABC is equilateral
∠CAD ≅ ∠ABE ≅ ∠BCF
Prove ∆DEF is equilateral
Answer:


Maintaining Mathematical Proficiency
Use the given property to complete the statement.
Question 42.
Reflexive Property of Congruence (Theorem 2. 1): ________ ≅ \(\overline{S E}\)
Answer:
\(\overline{S E}\) ≅ \(\overline{S E}\)
Question 43.
Symmetric Property of Congruence (Theorem 2.1): If ________ ≅ ________, then \(\overline{R S}\) ≅ \(\overline{J K}\)
Answer:
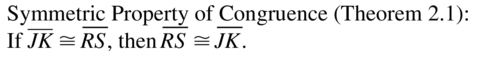
Question 44.
Transitive Property of Congruence (Theorem 2.1): If \(\overline{E F}\) ≅ \(\overline{P Q}\), and \(\overline{P Q}\) ≅ \(\overline{U V}\) ________ ≅ ________.
Answer:
Transitive Property of Congruence (Theorem 2.1): If \(\overline{E F}\) ≅ \(\overline{P Q}\), and \(\overline{P Q}\) ≅ \(\overline{U V}\), then \(\overline{U V}\) ≅ \(\overline{E F}\).
5.1 to 5.4 Quiz
Find the measure of the exterior angle.
Question 1.
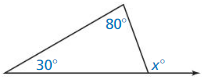
Answer:
x° = 180° – (180° – (30° + 80°))
= 180° – (180° – 110°)
= 180° – 70°
= 110°
Question 2.
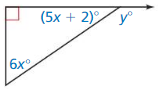
Answer:
90° + 5x + 2 + 6x = 180°
11x + 92 = 180°
11x = 180 – 92
11x = 88
x = 8°
y° = 180° – (5(8) + 2)
= 180° – 42
y° = 138°
Question 3.
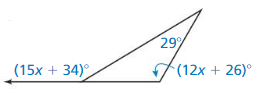
Answer:
29 + 12x + 26 + third_angle = 180
third_angle = 180 – 55 – 12x = 125 – 12x
15x + 34 = 180 – (125 – 12x)
15x + 34 = 180 – 125 + 12x
15x – 12x = 55 – 34
3x = 21
x = 7
15x + 34 = 15(7) + 34
= 105 + 34 = 139
Identify all pairs of congruent corresponding parts. Then write another congruence statement for the polygons.
Question 4.
∆ABC ≅ ∆DEF
Answer:
∠C = ∠F, ∠B = ∠E, ∠A = ∠D
Question 5.
QRST ≅ WXYZ
Answer:
∠Q = ∠W, ∠R = ∠X, ∠S = ∠Y, ∠T = ∠Z
Decide whether enough information is given to prove that the triangles are congruent using the SAS Congruence Theorem (Thm 5.5). If so, write a proof. If not, explain why.
Question 6.
∆CAD, ∆CBD
Answer:
∠A ≅ ∠B, AD ≅ BD, CD ≅ CD (Reflexive Property)
∆CAD ≅ ∆CBD by the SAS Congruence Theorem.
Question 7.
∆GHF, ∆KHJ
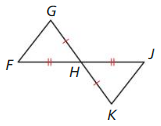
Answer:
GH ≅ HK, FH ≅ HJ and ∠GHF ≅ ∠JHK
∆GHF ≅ ∆KHJ by the SAS Congruence Theorem.
Question 8.
∆LWP, ∆NMP
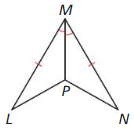
Answer:
LM ≅ MN, MP ≅ MP by reflexive property
∠LMP ≅ ∠PMN
∆LWP ≅ ∆NMP by the SAS Congruence Theorem.
Copy and complete the statement. State which theorem you used.
Question 9.
If VW ≅ WX, then ∠______ ≅ ∠ ________.
Answer:
If VW ≅ WX, then ∠V ≅ ∠X.
Question 10.
If XZ ≅ XY. then∠______ ≅ ∠ ________.
Answer:
If XZ ≅ XY. then∠Y ≅ ∠Z.
Question 11.
If ∠ZVX ≅∠ZXV, then ∠_______ ≅ ∠_______.
Answer:
If ∠ZVX ≅∠ZXV, then ∠ZV ≅ ∠ ZX.
Question 12.
If ∠XYZ ≅∠ZXY, then ∠______ ≅ ∠ ________.
Answer:
If ∠XYZ ≅∠ZXY, then ∠XY ≅ ∠ ZX.
Find the values of x and y.
Question 13.
∆DEF ≅ ∆QRS
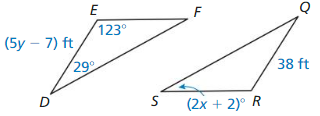
Answer:
EF ≅ SR, ED ≅ RQ, DF ≅ SQ
5y – 7 = 38
5y = 45
y = 9
123 + 29 + 2x + 2 = 180
154 + 2x = 180
2x = 28
x° = 14°
Question 14.
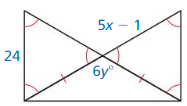
Answer:
5x – 1 = 24
5x = 25
x = 5
2 • 6y° = 360° – (60° + 60°) = 240
y = 20°
Question 15.
In a right triangle, the measure of one acute angle is 4 times the difference of the measure of the other acute angle and 5. Find the measure ol each acute angle in the triangle. (Section 5.1)
Answer:
Assuming the measure of the first acute angle equals x
The measure of the second acute angle = 4(x – 5)
x + 4(x – 5) = 90
5x – 20 = 90
5x = 110
x = 22
The first angle = 22°
The second angle = 90 – 22 = 68°
Question 16.
The figure shows a stained glass window. (Section 5.1 and Section 5.3)
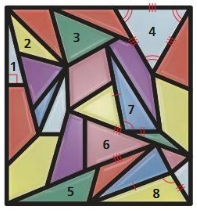
a. Classify triangles 1 – 4 by their angles.
Answer:
Triangle 1 is a right-angled trinagle, 2 is an acute angle triangle, 3 is an obtuse angle triangle and 4 is an equilateral triangle.
b. Classify triangles 4 – 6 by their sides.
Answer:
Triangle 4 is an equilateral triangle, 5 is a scalene triangle, 6 is an isosceles triangle.
c. Is there enough information given to prove that ∆7 ≅ ∆8? If so, label the vertices
and write a proof. If not, determine what additional information is needed.
Answer:
Yes, two congruent sides and one congruent angle.
By Side Angle Side Congruent Theorem, ∆7 ≅ ∆8.
5.5 Proving Triangle Congruence by SSS
Exploration 1
Drawing Triangles
Work with a partner.
Use dynamic geometry software.
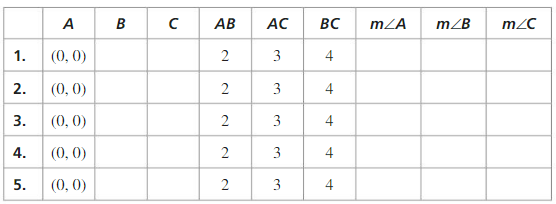
a. Construct circles with radii of 2 units and 3 units centered at the origin. Label the origin A. Then draw \(\overline{B C}\) of length 4 units.
Answer:
b. Move \(\overline{B C}\) so that B is on the smaller circle and C is on the larger circle. Then draw ∆ABC.
Answer:
c. Explain why the side lengths of ∆ABC are 2, 3, and 4 units.
Answer:
d. Find m∠A, m∠B, and m∠C.
Answer:
e. Repeat parts (b)and (d) several times, moving \(\overline{B C}\) to different locations. Keep track of ‘our results by copying and completing the table below. What can you conclude?
USING TOOLS STRATEGICALLY
To be proficient in math, you need to use technology to help visualize the results of varying assumptions, explore consequences, and compare predictions with data.
Answer:
Communicate Your Answer
Question 2.
What can you conclude about two triangles when you know the corresponding sides are congruent?
Answer:
Question 3.
How would you prove your conclusion in Exploration 1(e)?
Answer:
Lesson 5.5 Proving Triangle Congruence by SSS
Monitoring Progress
Decide whether the congruence statement is true. Explain your reasoning.
Question 1.
∆DFG ≅ ∆HJK
Answer:
DG ≅ HK, DF ≅ HJ, FG ≅ JK
According to SSS Congruence Theorem, ∆DFG ≅ ∆HJK.
Question 2.
∆ACB ≅ ∆CAD
Answer:
AB ≅ CD, AD ≅ BC, AC ≅ AC by reflexive property
So, ∆ACB ≅ ∆CAD by SSS Congruence Theorem
Question 3.
∆QPT ≅ ∆RST
Answer:
QT ≅ TR, PQ ≅ SR, PT ≅ ST
So, ∆QPT ≅ ∆RST by SSS Congruence Theorem
Determine whether the figure is stable. Explain your reasoning.
Question 4.

Answer:
The figure is not stable. Because it doesn’t have a triangle. By the SSS Congruence Theorem, those triangles cannot change shape.
Question 5.

Answer:
The figure is stable as the diagonal forms the triangle. By the SSS Congruence Theorem, these triangles cannot change the shape.
Question 6.

Answer:
The figure is stable as the diagonal forms the triangle. By the SSS Congruence Theorem, these triangles cannot change the shape.
Use the diagram.
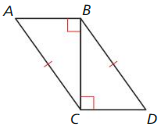
Question 7.
Redraw ∆ABC and ∆DCB side by side with corresponding parts in the same position.
Answer:
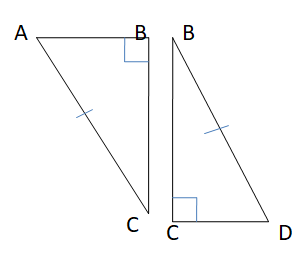
Question 8.
Use the information in the diagram to prove that ∆ABC ≅ ∆DCB.
Answer:
AC ≅ BD, BC ≅ BC by reflexive property of congruence, and AB ≅ CD
So, ∆ABC ≅ ∆DCB by SSS Congruence Theorem.
Exercise 5.5 Proving Triangle Congruence by SSS
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The side opposite the right angle is called the __________of the right triangle.
Answer:
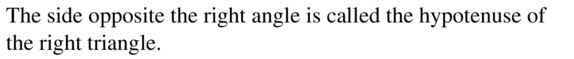
Question 2.
WHICH ONE DOESNT BELONG?
Which triangles legs do not belong with the other three? Explain your reasoning.

Answer:
The second triangle legs do not belong with the other three.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4, decide whether enough information is given to prove that the triangles are congruent using the SSS Congruence Theorem (Theorem 5.8). Explain.
Question 3.
∆ABC, ∆DBE
Answer:
![]()
Question 4.
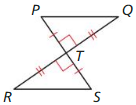
∆PQS, ∆RQS
Answer:
No, PQ ≅ QR, QS ≅ QS by reflexive property.
We need one more congruence property to prove those triangles are congruent.
In Exercises 5 and 6, decide whether enough information is given to prove that the triangles are congruent using the HL Congruence Theorem (Theorem 5.9). Explain.
Question 5.
∆ABC, ∆FED
Answer:
![]()
Question 6.
∆PQT, ∆SRT
Answer:
PT ≅ TS, RT ≅ TQ, ∠PTQ ≅ ∠RTS
∆PQT ≅ ∆SRT by SAS congruence theorem.
In Exercises 7-10. decide whether the congruence statement is true. Explain your reasoning.
Question 7.
∆RST ≅ ∆TQP
Answer:
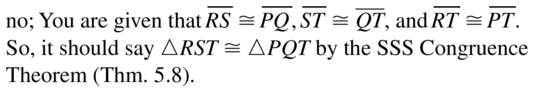
Question 8.
∆ABD ≅ ∆CDB
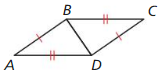
Answer:
AB ≅ CD, AD ≅ BC
BD ≅ BD by reflexive property of congruence
∆ABD ≅ ∆CDB by SSS Congruence theorem.
Question 9.
∆DEF ≅ ∆DGF
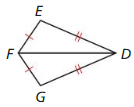
Answer:
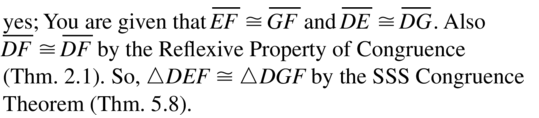
Question 10.
∆JKL ≅ ∆LJM
Answer:
KJ ≅ LM, KL ≅ JM
JL ≅ JL by reflexive property of congruence
So, ∆JKL ≅ ∆LJM by SSS Congruence Theorem.
In Exercises 11 and 12, determine whether the figure is stable. Explain your reasoning.
Question 11.

Answer:

Question 12.

Answer:
No, the figure is not stable.
In Exercises 13 and 14, redraw the triangles so they are side by side with corresponding parts in the same position. Then write a proof.
Question 13.
Given \(\overline{A C}\) ≅ \(\overline{B D}\)
\(\overline{A B}\) ⊥ \(\overline{A D}\)
\(\overline{C D}\) ⊥ \(\overline{A D}\)
Prove ∆BAD ≅ ∆CDA
Answer:

Question 14.
Given G is the midpoint of \(\overline{E H}\), \(\overline{F G}\) ≅ \(\overline{G I}\), ∠E and ∠H are right angles.
Prove ∆EFG ≅ ∆HIG
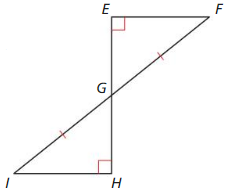
Answer:
EG ≅ GH as G is the midpoint of \(\overline{E H}\)
\(\overline{F G}\) ≅ \(\overline{G I}\), ∠E ≅ ∠H
∆EFG ≅ ∆HIG by SAS congruence theorem.
In Exercises 15 and 16. write a proof.
Question 15.
Given \(\overline{L M}\) ≅ \(\overline{J K}\), \(\overline{M J}\) ≅ \(\overline{K L}\)
Prove ∆LMJ ≅ ∆JKL
Answer:

Question 16.
Given \(\overline{W X}\) ≅ \(\overline{V Z}\), \(\overline{W Y}\) ≅ \(\overline{V Y}\), \(\overline{Y Z}\) ≅ \(\overline{Y X}\)
Prove ∆VWX ≅ ∆WVZ
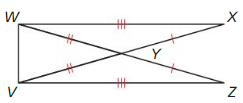
Answer:
XY ≅ YZ, WY ≅ VY, WX ≅ VZ
∆VWX ≅ ∆WVZ by SSS Congruence theorem
CONSTRUCTION
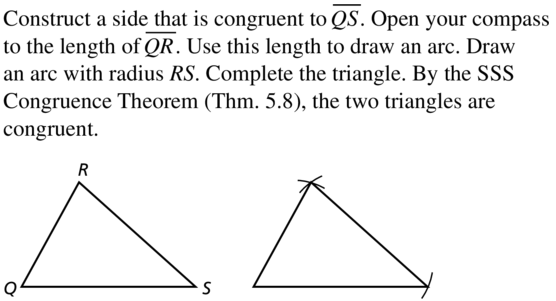
In Exercises 17 and 18, construct a triangle that is congruent to ∆QRS using the SSS Congruence Theorem Theorem 5.8).
Question 17.
Answer:
Question 18.
Answer:
At first, construct a side that is congruent to QS. Draw an arc with the compass with Q as center and radius as QR. Draw another arc that intersects the first arc with S as center and radius as SR. Join the point to Q and S to form a circle that is congruent to ∆QRS.
Question 19.
ERROR ANALYSIS
Describe and correct the error in identifying congruent triangles.
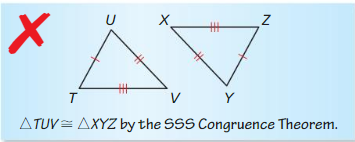
Answer:

Question 20.
ERROR ANALYSIS
Describe and correct the error in determining the value of x that makes the triangles congruent.
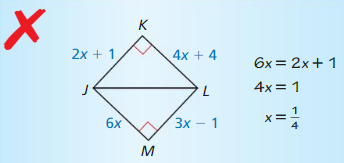
Answer:
4x + 4 = 6x
2x = 4
x = 2
Question 21.
MAKING AN ARGUMENT
Your friend claims that in order to use the SSS Congruence Theorem (Theorem 5.8) Lo prove that two triangles are congruent, both triangles must be equilateral triangles. Is your friend correct? Explain your reasoning.
Answer:

Question 22.
MODELING WITH MATHEMATICS
The distances between consecutive bases on a softball field are the same. The distance from home plate to second base is the same as the distance from first base to third base. The angles created at each base are 90°. Prove
∆HFS ≅ ∆FST ≅ ∆STH
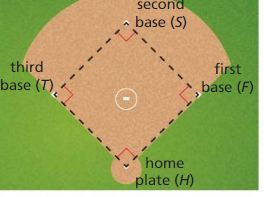
Answer:
HS ≅ FT
FS ≅ FS (reflexive property of congruence)
∠HFS ≅ ∠TFS
∆HFS ≅ ∆FST (SAS congruence theorem)
ST ≅ ST (reflexive property of congruence)
HS ≅ FT
∠FST ≅ ∠TSH
So, ∆FST ≅ ∆STH (SAS congruence theorem)
Therefore, ∆HFS ≅ ∆FST ≅ ∆STH
Question 23.
REASONING
To support a tree you attach wires from the trunk of the tree to stakes in the ground, as shown in the diagram.
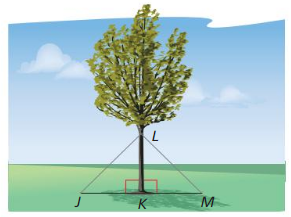
a. What additional information do you need to use the HL Congruence Theorem (Theorem 5.9) to prove that ∆JKL ≅ ∆MKL?
b. Suppose K is the midpoint of JM. Name a theorem you could use to prove that ∆JKL ≅ ∆MKL. Explain your reasoning.
Answer:

Question 24.
REASONING
Use the photo of the Navajo rug, where \(\overline{B C}\) ≅ \(\overline{D E}\) and \(\overline{A C}\) ≅ \(\overline{C E}\)

a. What additional intormation do you need to use the SSS Congruence Theorem (Theorem 5.8) to prove that ∆ABC ≅ ∆CDE?
b. What additional information do you need to use the HL Congruence Theorem (Theorem 5.9) to prove that ∆ABC ≅ ∆CDE?
Answer:
a. AB ≅ CD is required o use the SSS Congruence Theorem (Theorem 5.8) to prove that ∆ABC ≅ ∆CDE
b. One angle should be the right angle in those triangles to use the HL Congruence Theorem (Theorem 5.9) to prove that ∆ABC ≅ ∆CDE
In Exercises 25-28. use the given coordinates to determine whether ∆ABC ≅ ∆DEF.
Question 25.
A(- 2, – 2), B(4, – 2), C(4, 6), D(5, 7), E(5, 1), F(13, 1)
Answer:
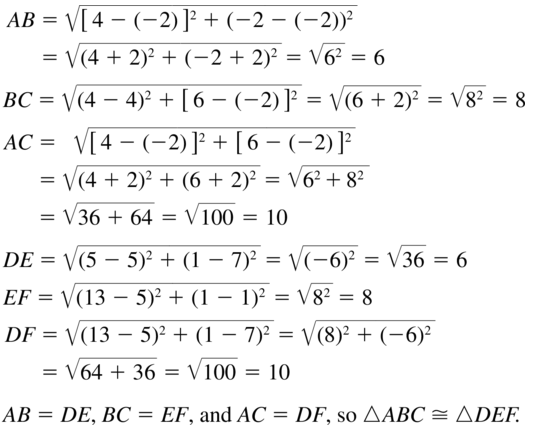
Question 26.
A(- 2, 1), B(3, – 3), C(7, 5), D(3, 6), E(8, 2), F( 10, 11)
Answer:
AB = √(3 + 2)² + (-3 – 1)²
= √25 + 16 = √41
BC = √(7 – 3)² + (5 + 3)²
= √16 + 64 = √80 = 8.9
AC = √(7 + 2)² + (5 – 1)²
= √81 + 16 = √97 = 9.8
DE = √(8 – 3)² + (2 – 6)²
= √25 + 16 = √41
EF = √(10 – 8)² + (11 – 2)²
= √4 + 81 = √85 = 9.2
DF = √(10 – 3)² + (11 – 6)²
= √49 + 25 = √74 = 8.6
AB ≅ DE, BC ≅ EF, AC ≇ DF. So, ∆ABC ≇ ∆DEF
Question 27.
A(0, 0), B(6, 5), C(9, 0), D(0, – 1), E(6, – 6), F(9, – 1)
Answer:
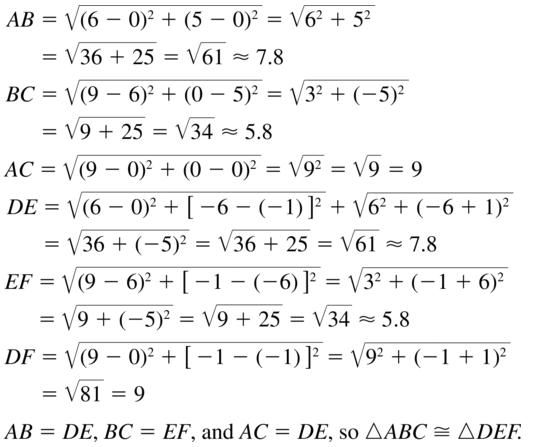
Question 28.
A(- 5, 7), B(- 5, 2), C(0, 2), D(0, 6), E(0, 1), F(4, 1)
Answer:
AB = √(-5 + 5)² + (2 – 7)² = √0 + 25 = 5
BC = √(0 + 5)² + (2 – 2)² = √0 + 25 = 5
AC = √(0 + 5)² + (2 – 7)² = √25 + 25 = √50
DE = √(0 – 0)² + (1 – 6)² = √0 + 25 = 5
EF = √(0 – 4)² + (1 – 1)² = √0 + 16 = 4
DF = √(4 – 0)² + (1 – 6)² = √16 + 25 = √41
AB = DE, BC ≅ EF, AC ≅ DF.
So, ∆ABC ≅ ∆DEF by SSS Congruence theorem.
Question 29.
CRITICAL THINKING
You notice two triangles in the tile floor of a hotel lobby. You want to determine whether the triangles are congruent. but you only have a piece of string. Can you determine whether the triangles are congruent? Explain.
Answer:

Question 30.
HOW DO YOU SEE IT?
There are several theorems you can use to show that the triangles in the “square” pattern are congruent. Name two of them.

Answer:
Question 31.
MAKING AN ARGUMENT
Your cousin says that ∆JKL is congruent to ∆LMJ by the SSS Congruence Theorem (Thm. 5.8). Your friend says that ∆JKL is congruent to ∆LMJ by the HL Congruence Theorem (Thm. 5.9). Who is correct? Explain your reasoning.
Answer:

Question 32.
THOUGHT PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry. all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry. do you think that two triangles are congruent if their corresponding sides are congruent? Justify your answer.
Answer:
USING TOOLS
In Exercises 33 and 34, use the given information to sketch ∆LMN and ∆STU. Mark the triangles with the given information.
Question 33.
![]()
Answer:
Question 34.
![]()
Answer:
Question 35.
CRITICAL THINKING
The diagram shows the light created by two spotlights, Both spotlights are the same distance from the stage.
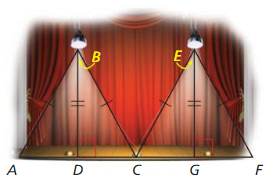
Answer:
a. Show that ∆ABD ≅ ∆CBD. State which theorem or postulate you used and explain your reasoning.
b. Are all four right triangles shown in the diagram Congruent? Explain your reasoning.
Answer:

Question 36.
MATHEMATICAL CONNECTIONS
Find all values of x that make the triangles congruent. Explain.
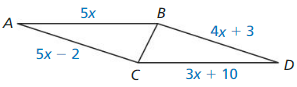
Answer:
5x = 4x + 3
5x – 4x = 3
x = 3
5x – 2 = 3x + 10
2x = 12
x = 6
5x – 2 = 4x + 3
x = 5
5x = 3x + 10
2x = 10
x = 5
The possible values of x are 3, 6, 5.
Maintaining Mathematical proficiency
Use the congruent triangles.
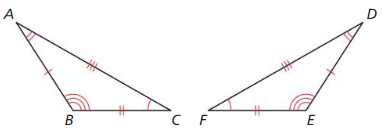
Question 37.
Name the Segment in ∆DEF that is congruent to \(\overline{A C}\).
Answer:
![]()
Question 38.
Name the segment in ∆ABC that is congruent to \(\overline{E F}\).
Answer:
BC is congruent to EF.
Question 39.
Name the angle in ∆DEF that is congruent to ∠B.
Answer:
![]()
Question 40.
Name the angle in ∆ABC that is congruent to ∠F.
Answer:
∠C is congruent to ∠F.
5.6 Proving Triangle Congruence by ASA and AAS
Exploration 1
Determining Whether SSA Is Sufficient
Work with a partner.
a. Use dynamic geometry software to construct ∆ABC. Construct the triangle so that vertex B is at the origin. \(\overline{A B}\) has a length of 3 units. and \(\overline{B C}\) has a length of 2 units.
Answer:
b. Construct a circle with a radius of 2 units centered at the origin. Locate point D where the circle intersects \(\overline{A C}\). Draw \(\overline{B D}\).
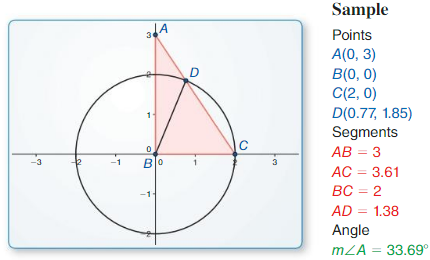
Answer:
c. ∆ABC and ∆ABD have two congruent sides and a non included congruent angle.
Name them.
Answer:
d. Is ∆ABC ≅ ∆ABD? Explain your reasoning.
Answer:
e. Is SSA sufficient to determine whether two triangles are congruent? Explain your reasoning.
Answer:
Exploration 2
Determining Valid Congruence Theorems
Work with a partner. Use dynamic geometry software to determine which of the following are valid triangle congruence theorems. For those that are not valid. write a counter example. Explain your reasoning.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to recognize and use counterexamples.
| Possible Congruence Theorem | Valid or not valid? |
| SSS | |
| SSA | |
| SAS | |
| AAS | |
| ASA | |
| AAA |
Answer:
Communicate Your Answer
Question 3.
What information is sufficient to determine whether two triangles are congruent?
Answer:
- It is required to provide sufficient information to determine whether two triangle are congruent.
- If all the three sides of two triangles are equal, then the two triangles are congruent. Triangles are said to be congruent by SSS congruency or SSS congruence.
- If two sides and including angle of two triangles are equal, then the two triangles are congruent. Triangles are said to be congruent by AAS congruency or ASA congruency or ASA congruency.
Question 4.
Is it possible to show that two triangles are congruent using more than one congruence theorem? If so, give an example.
Answer:
1. Proving ΔABC ≅ ΔBAD using ASA
In ΔABC and ΔBAD
∠CBA = ∠DAB
ASA Congruence theorem, ΔABC and ΔBAD are congruent.
2. Proving ΔABC and ΔBAD using SSS
ΔABC and ΔBAD
AC = BD (equivalent sides of equivalent triangles)
AB = AB (Common side)
BC = AD (equivalent sides of equivalent triangles)
ΔABC and ΔBAD are congruent
Lesson 5.6 Proving Triangle Congruence by ASA and AAS
Monitoring Progress
Question 1.
Can the triangles be proven congruent with the information given in the diagram? If so, state the theorem you would use.
Answer:
WX ≅ YZ, XY ≅ WZ, and ∠1 ≅ ∠3
So, WXY ≅ WYZ by the AAS congruence theorem.
Question 2.
In the diagram, \(\overline{A B}\) ⊥ \(\overline{A D}\), \(\overline{D E}\) ⊥ \(\overline{A D}\), and \(\overline{A C}\) ≅ \(\overline{D C}\) . Prove ∆ABC ≅ ∆DEF.
Answer:
\(\overline{A C}\) ≅ \(\overline{D C}\), ∠A ≅ ∠D
So, the given information is not enough to prove that ∆ABC ≅ ∆DEF.
Question 3.
In the diagram, ∠S ≅ ∠U and \(\overline{B D}\)\(\overline{B D}\) . Prove that ∆RST ≅ ∆VYT
Answer:
∠S ≅ ∠U, RS ≅ UV
So, the given information is not enough to prove that ∆RST ≅ ∆VYT
Lesson 5.6 Proving Triangle Congruence by ASA and AAS
Vocabulary and Core Concept Check
Question 1.
WRITING
How arc the AAS Congruence Theorem (Theorem 5. 11) and the ASA Congruence
Theorem (Theorem 5.10) similar? How are they different?
Answer:

Question 2.
WRITING
You know that a pair of triangles has two pairs of congruent corresponding angles. What other information do you need to show that the triangles are congruent?
Answer:
In order to use the AAS or ASA Congruence theorem, you need to know that two pairs of corresponding angles and one more pair of corresponding sides are congruent.
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, decide whether enough information is given to prove that the triangles are congruent. If so, state the theorem you would use.
Question 3.
∆ABC, ∆QRS
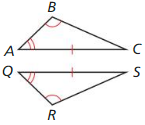
Answer:
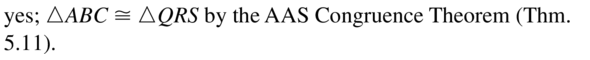
Question 4.
∆ABC, ∆DBC
Answer:
No, two angles are not sufficient to determine congruence.
Question 5.
∆XYZ, ∆JKL
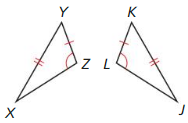
Answer:
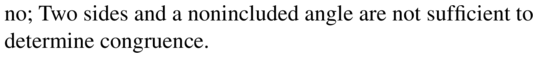
Question 6.
∆RSV, ∆UTV
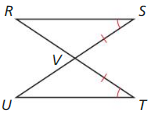
Answer:
No, one side and one included angle is not sufficient to determine congruence.
In Exercises 7 and 8, state the third congruence statement that is needed to prove that ∆FGH ≅ ∆LMN the given theorem.
Question 7.
Given \(\overline{G H}\) ≅ \(\overline{M N}\), ∠G ≅ ∠M, _______ = ________
Use the AAS Congruence Theorem (Thm. 5.11).
Answer:
![]()
Question 8.
Given \(\overline{F G}\) ≅ \(\overline{L M}\), ∠G ≅ ∠M, _______ = ________
Use the ASA Congruence Theorem (Thm. 5.10).
Answer:
\(\overline{F G}\) ≅ \(\overline{L M}\), ∠G ≅ ∠M, ∠F ≅ ∠L
In Exercises 9 – 12. decide whether you can use the given information to prove that ∆ABC ≅ ∆DEF Explain your reasoning.
Question 9.
∠A ≅ ∠G, ∠C ≅∠F, \(\overline{A C}\) ≅ \(\overline{D F}\)
Answer:

Question 10.
∠C ≅ ∠F, \(\overline{A B}\) ≅ \(\overline{D E}\), \(\overline{B C}\) ≅ \(\overline{E F}\)
Answer:
Yes, ∆ABC ≅ ∆DEF by SAS congruence theorem
Question 11.
∠B ≅ ∠E, ∠C ≅∠F, \(\overline{A C}\) ≅ \(\overline{D E}\)
Answer:
![]()
Question 12.
∠A ≅ ∠D, ∠B ≅∠E, \(\overline{B C}\) ≅ \(\overline{E F}\)
Answer:
Yes, ∆ABC ≅ ∆DEF by AAS theorem.
CONSTRUCTION
In Exercises 13 and 14, construct a triangle that is congruent to the given triangle using the ASA Congruence Theorem (Theorem 5.10). Use a compass and straightedge.
Question 13.
Answer:

Question 14.
Answer:
Construct a side that is similar to JK. With J as center and JL as radius, draw an arc. With K as center and KL as radius draw another arc that intersects the first arc. Label the intersection of arcs as L. Connect LK and LJ.
ERROR ANALYSIS
In Exercises 15 and 16, describe and correct the error.
Question 15.
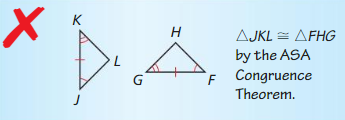
Answer:

Question 16.
Answer:
△QRS ≅ △VWX by ASA congruence theorem.
PROOF
In Exercises 17 and 18, prove that the triangles are congruent using the ASA Congruence Theorem (Theorem 5.10).
Question 17.
Given M is the midpoint of \(\overline{N L}\).
![]()
Prove ∆NQM ≅ ∆MPL
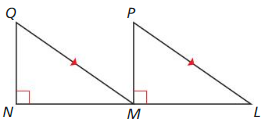
Answer:
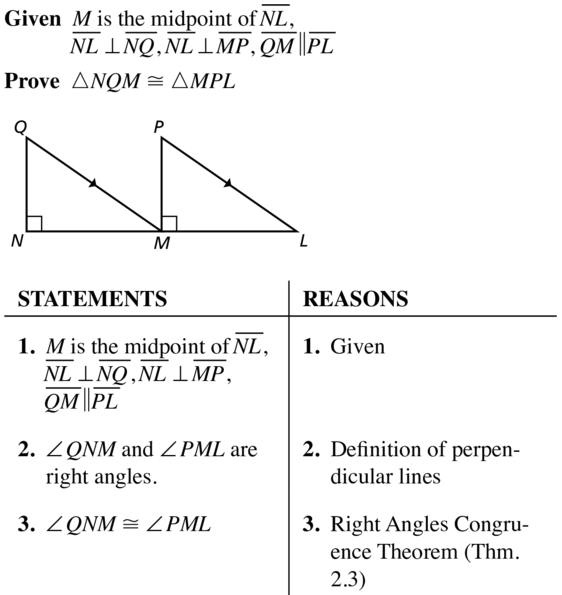

Question 18.
Given \(\overline{A J}\) ≅ \(\overline{K C}\) ∠BJK ≅ ∠BKJ, ∠A ≅ ∠C
Prove ∆ABK ≅ ∆CBJ
Answer:
AJ ≅ KC, ∠K ≅ ∠J, ∠A ≅ ∠C
So, ∆ABK ≅ ∆CBJ by ASA congruence theorem.
PROOF
In Exercises 19 and 20, prove that the triangles are congruent using the AAS Congruence Theorem (Theorem 5.11).
Question 19.
Given \(\overline{V W}\) ≅ \(\overline{U W}\), ∠X ≅ ∠Z
Prove ∆XWV ≅ ∆ZWU
Answer:
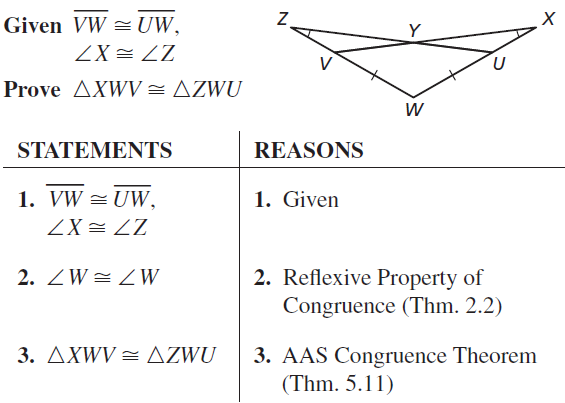
Question 20.
Given ∠NKM ≅∠LMK, ∠L ≅∠N
Prove ∆NMK ≅ ∆LKM
Answer:
Given ∠NKM ≅∠LMK, ∠L ≅∠N
KM ≅ KM ≅ by reflexive property of congruence
∆NMK ≅ ∆LKM by AAS congruence theorem.
PROOF
In Exercises 21-23, write a paragraph proof for the theorem about right triangles.
Question 21.
Hypotenuse-Angle (HA) Congruence Theorem
If an angle and the hypotenuse of a right triangle are congruent to an angle and the hypotenuse of a second right triangle, then the triangles are congruent.
Answer:

Question 22.
Leg-Leg (LL) Congruence Theorem
If the legs of a right triangle are congruent to the legs of a second right triangle, then the triangles are congruent.
Answer:
You are given that egs of a right triangle are congruent to the legs of a second right triangle so triangles are congruent by LL congruence theorem.
Question 23.
Angle-Leg (AL) Congruence Theorem
If an angle and a leg of a right triangle are congruent to an angle and a leg of a second right triangle, then the triangles are Congruent.
Answer:

Question 24.
REASONING
What additional in information do you need to prove ∆JKL ≅ ∆MNL by the ASA Congruence Theorem (Theorem 5. 10)?
(A) \(\overline{K M}\) ≅ \(\overline{K J}\)
(B) \(\overline{K H}\) ≅ \(\overline{N H}\)
(C) ∠M ≅ ∠J
(D) ∠LKJ ≅ ∠LNM
Answer:
Question 25.
MATHEMATICAL CONNECTIONS
This toy contains △ABC and △DBC. Can you conclude that △ABC ≅ △DBC from the given angle measures? Explain
m∠ABC = (8x – 32)°
m∠DBC = (4y – 24)°
m∠BCA = (5x + 10)°
m∠BCD = (3y + 2)°
m∠CAB = (2x – 8)°
m∠CDB = (y – 6)°
Answer:


Question 26.
REASONING
Which of the following congruence statements are true? Select all that apply.
(A) \(\overline{B D}\) ≅ \(\overline{B D}\)
(B) ∆STV ≅ ∆XVW
(C) ∆TVS ≅ ∆VWU
(D) ∆VST ≅ ∆VUW
Answer:
(C) ∆TVS ≅ ∆VWU by ASA congruence theorem.
∠T ≅ ∠V, TS ≅ VU, ∠S ≅ ∠U
(D) ∆VST ≅ ∆VUW by ASA congruence theorem.
∠T ≅ ∠V, TS ≅ VU, ∠S ≅ ∠U
Question 27.
PROVING A THEOREM
Prove the Converse of the Base Angles Theorem (Theorem 5.7). (Hint: Draw an auxiliary line inside the triangle.)
Answer:


Question 28.
MAKING AN ARGUMENT
Your friend claims to be able Lo rewrite any proof that uses the AAS Congruence Theorem (Thin. 5. 11) as a proof that uses the ASA Congruence Theorem (Thin. 5.10). Is this possible? Explain our reasoning.
Answer:
No your friend is not correct. Because the congruent side in AAS is not between the congruent angles and ASA has the congruent side between the two angles.
So they are not interchangeable.
Question 29.
MODELING WITH MATHEMATICS
When a light ray from an object meets a mirror, it is reflected back to your eye. For example, in the diagram, a light ray from point C is reflected at point D and travels back to point A. The law of reflection states that the angle of incidence, ∠CDB. is congruent to the angle of reflection. ∠ADB.
a. Prove that ∆ABD is Congruent to ∆CBD.
Given ∠CBD ≅∠ABD
DB ⊥ AC
Prove ∆ABD ≅ ∆CBD
b. Verify that ∆ACD is isosceles.
c. Does moving away from the mirror have an effect on the amount of his or her reflection a person sees? Explain.
Answer:


Question 30.
HOW DO YOU SEE IT?
Name as man pairs of congruent triangles as you can from the diagram. Explain how you know that each pair of triangles is congruent.
Answer:
ΔPTS and ΔQTR
PT = RT
ST = QT
PS = QR
ΔPTS ≅ ΔQTR
ΔPTQ and ΔRTS
RT = PT
PQ = SR
QT = ST
ΔPTQ ≅ ΔRTS
Question 31.
CONSTRUCTION
Construct a triangle. Show that there is no AAA congruence rule by constructing a second triangle that has the same angle measures but is not congruent.
Answer:
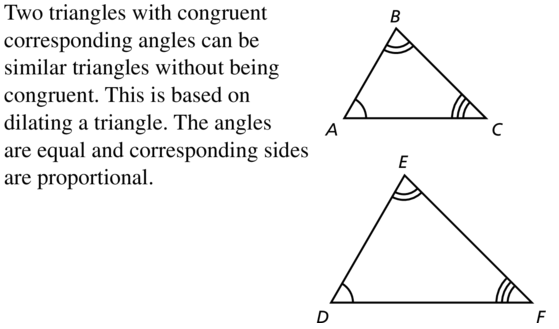
Question 32.
THOUGHT PROVOKING
Graph theory is a branch of mathematics that studies vertices and the way they are connected. In graph theory. two polygons are isomorphic if there is a one-to-one mapping from one polygon’s vertices to the other polygon’s vertices that preserves adjacent vertices. In graph theory, are any two triangles isomorphic? Explain your reasoning. second triangle that has the same angle measures but is not congruent.
Answer:
Yes, any two congruent triangles can show isomorphism because the corresponding vertices can be mapped on to each other to completely overlap each other as required for isomorphism.
Question 33.
Mathematical Connections
Six statements are given about ∆TUV and ∆XYZ
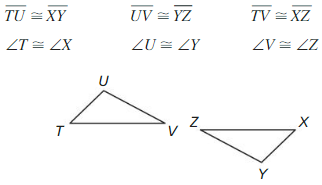
a. List all combinations of three given statements that could provide enough information to prove that ∆TUV is congruent to ∆XYZ.
b. You choose three statements at random. What is the probability that the statements you choose provide enough information to prove that the triangles are congruent?
Answer:


Maintaining Mathematical proficiency
Find the coordinates of the midpoint of the line segment with the given endpoints.
Question 34.
C(1, 0) and D(5, 4)
Answer:
Given points C(1, 0) and D(5, 4)
Midpoint = (\(\frac { 1 + 5 }{ 2 } \), \(\frac { 0 + 4 }{ 2 } \)) = (\(\frac { 6 }{ 2 } \), \(\frac { 4 }{ 2 } \)) = (3, 3)
Question 35.
J(- 2, 3) and K(4, – 1)
Answer:
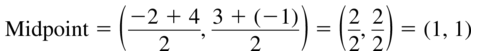
Question 36.
R(- 5, – 7) and S(2, – 4)
Answer:
Midpoint = (\(\frac { -5 + 2 }{ 2 } \), \(\frac { -7 – 4 }{ 2 } \)) = (\(\frac { -3 }{ 2 } \), \(\frac { -11 }{ 2 } \))
Copy and angle using a compass and straightedge.
Question 37.
Answer:
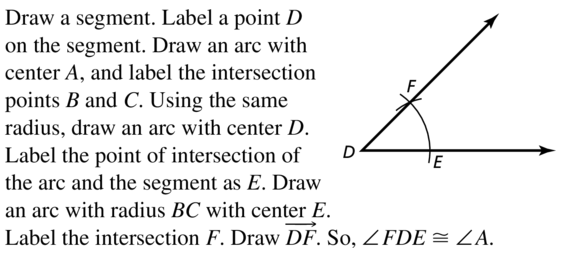
Question 38.
Answer:
Draw a segment. Label a point D on the segment.
Draw an arc with center B, and label the intersection points A and C.
Using the same radius, draw an arc with center D.
Label the point of intersection of the arc with radius BC with center D.
Label the intersection F. Draw DF. So, ∠B ≅ ∠FDE.
5.7 Using Congruent Triangles
Exploration 1
Measuring the Width of a River
Work with a partner:
The figure shows how a surveyor can measure the width of a river by making measurements on only one side of the river.
a. Study the figure. Then explain how the surveyor can find the width of the river.
Answer:
b. Write a proof to verify that the method you described in part (a) is valid.
Given ∠A is a right angle, ∠D is a right angle, \(\overline{A C}\) ≅ \(\overline{C D}\)
Answer:
c. Exchange Proofs with your partner and discuss the reasoning used.
CRITIQUING THE REASONING OF OTHERS
To be proficient in math, you need to listen to or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments.
Answer:
Exploration 2
Measuring the Width of a River
Work with a partner. It was reported that one of Napoleon’s offers estimated the width of a river as follows. The officer stood on the hank of the river and lowered the visor on his cap until the farthest thin visible was the edge of the bank on the other side. He then turned and rioted the point on his side that was in line with the tip of his visor and his eye. The officer then paced the distance to this point and concluded that distance was the width of the river.
a. Study the figure. Then explain how the officer concluded that the width of the river is EG.
Answer:
b. Write a proof to verify that the conclusion the officer made is correct.
Given ∠DEG is a right angle, ∠DEF is a right angle, ∠EDG ≅ ∠EDF
Answer:
c. Exchange proofs with your partner and discuss the reasoning used.
Answer:
Communicate Your Answer
Question 3.
How can you use congruent triangles to make an indirect measurement?
Answer:
Congruent triangles can be used to do indirect measurement as the measurements of congruent triangles are always equal, by calculating the measurement of one triangle, the measurement of another triangle will be automatically obtained as they are equal to the calculated measurements.
Question 4.
Why do you think the types of measurements described in Explorations 1 and 2 are called indirect measurements?
Answer:
Since, in explorations 1 and 2, the direct measurement of the length of the river is not possible, so we used the concept of similarity to measure distance indirectly.
We used the concept of congruent triangles to find the length of the river indirectly, that’s why the types of measurements described in Explorations 1 and 2 are called indirect measurements.
Lesson 5.7 Using Congruent Triangles
Monitoring Progress
Question 1.
Explain how you can prove that ∠A ≅ ∠C.
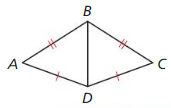
Answer:
If you can prove that △ABD ≅ △CBD, then ∠A ≅ ∠C.
AB ≅ BC, AD ≅ CD
BD ≅ BD by reflexive property of congruence
So, △ABD ≅ △CBD by SSS congruence theorem.
Question 2.
In Example 2, does it mailer how far from point N you place a stake at point K? Explain.
Answer:
Change the placement of the stake at point K away from the original point.
The midpoint M changes but the congruency remain the same.
Similarly, move point K close to N.
The midpoint changes but the congruency is not affected.
Question 3.
Write a plan to prove that ∆PTU ≅ ∆UQP.
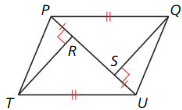
Answer:
TU ≅ PQ
∠PTU ≅ ∠UQP
PU ≅ PU by reflexive property of congruence
∆PTU ≅ ∆UQP by SAS congruence theorem.
Question 4.
Use the construction of an angle bisector on page 42. What segments can you assume are congruent?
Answer:
Refer to angle bisector on page 42.
Distance from A to B is same as A to C.
Thus AB and AC line segments have the same length.
Since the line segments, AB and AC have same length.
AB ≅ AC
Also, ∠CAG = ∠GAB (since AG is angle bisector)
∠CAG ≅ ∠GAB
Exercise 5.7 Using Congruent Triangles
Vocabulary and core concept check
Question 1.
COMPLETE THE SENTENCE
_____________ parts of congruent triangle are congruent.
Answer:
![]()
Question 2.
WRITING
Describe a situation in which you might choose to use indirect measurement with
congruent triangles to find a measure rather than measuring directly.
Answer:
Indirect measurements are calculations based on known lengths.
When two triangles are similar using AAS, SSS, ASA or SAS indirect measurement can be used to find missing measurements and angles.
If you were given a triangle with two angles marked and a similar triangle with two sides marked you would be able to find measurements of the angles indirectly.
Monitoring Progress and Modeling With Mathematics
In Exercise 3-8, explain how to prove that the statement is true.
Question 3.
∠A ≅ ∠D
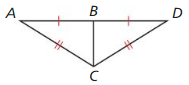
Answer:

Question 4.
∠Q ≅∠T
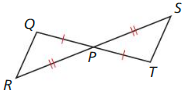
Answer:
QP ≅ PT, RP ≅ SP, QR ≅ ST
All pairs of sides are congruent by SSS congruence theorem. △QPR ≅ △STP.
∠Q ≅∠T.
Question 5.
\(\overline{J M}\) ≅ \(\overline{L M}\)
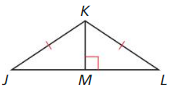
Answer:

Question 6.
\(\overline{A C}\) ≅ \(\overline{D B}\)
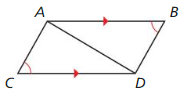
Answer:
\(\overline{A C}\) ≅ \(\overline{D B}\),
\(\overline{A D}\) ≅ \(\overline{A D}\) by reflexive property of congruence
∠C ≅∠B
△ACD ≅ △BDC by SAS congruence theorem.
Question 7.
\(\overline{G K}\) ≅ \(\overline{H J}\)
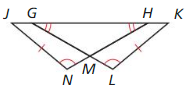
Answer:
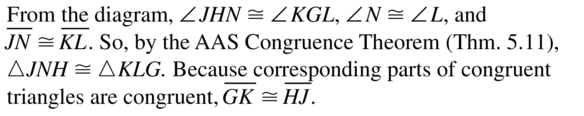
Question 8.
\(\overline{Q W}\) ≅ \(\overline{V T}\)
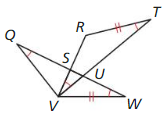
Answer:
VW ≅ RT, ∠Q ≅ ∠S, ∠W ≅ ∠T
△QVW ≅ △VRT by the AAS congruence theorem
So, \(\overline{Q W}\) ≅ \(\overline{V T}\)
In Exercises 9-12, write a plan to prove that ∠1 ≅∠2.
Question 9.
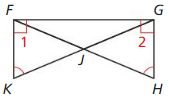
Answer:

Question 10.
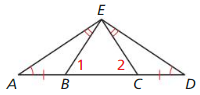
Answer:
∠A ≅ ∠D, AB ≅ CD and ∠BEA ≅ ∠CED
So, △ABE ≅ △EDC by AAS congruence theorem
∠ABE ≅ ∠DCE
Use the congruent complements theorem to prove that ∠1 ≅ ∠2
Question 11.
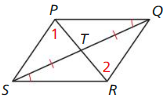
Answer:

Question 12.
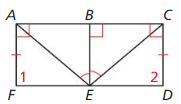
Answer:
AF ≅ CD, ∠AEF ≅ ∠CED, ∠FAE ≅ ∠ECD
So, △AFE ≅ △CDE by ASA congruence thorem
Then all parts of the triangles are congruent.
So, ∠1 ≅ ∠2
In Exercises 13 and 14. write a proof to verify that the construction is valid.
Question 13.
Line perpendicular to a line through a point not on the line
Plan for proof ∆APQ ≅ ∆BPQ by the congruence Theorem (Theorem 5.8). Then show the ∆APM ≅ ∆BPM using the SAS Congruence Theorem (Theorem 5.5). Use corresponding parts of congruent triangles to show that ∠AMP and ∠BMP are right angles.
Answer:


Question 14.
Line perpendicular to a line through a p0int on the line
Plan for Proof Show that ∆APQ ≅ ∆BPQ by the SSS Congruence Theorem (Theorem 5.8) Use corresponding parts of congruent triangles to show that ∠QPA and ∠QPB are right angles.
Answer:
In Exercises 15 and 16, use the information given in the diagram to write a proof.
Question 15.
Prove \(\overline{F L}\) ≅ \(\overline{H N}\)
Answer:
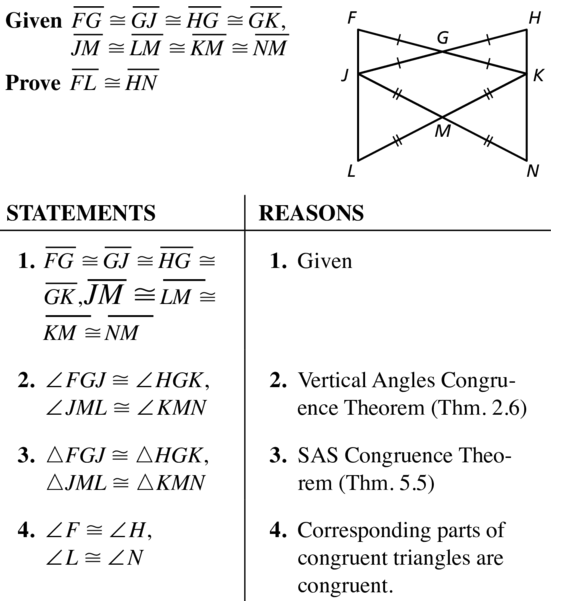

Question 16.
Prove ∆PUX ≅ ∆QSY
Answer:
Consider the side SU.
Show that SU is congruent to itself
SU ≅ SU
Consider the sides RS, VU and SU.
RS = VU
SU = SU
Consider the sides RU and VS.
RU = RS + SU
VS = VU + SU
Use the transitive property of equality
RU = VS
Consider the sides RU and VS
RU ≅ VS
∠URP ≅ ∠SVQ
RU ≅ VS
∠PUR ≅ ∠QSV
Consider the angles ∠URP and ∠URX
Consider the angles ∠SVQ and ∠SVY
The angles ∠URP and ∠URX form a linear pair.
The angles ∠SVQ and ∠SVY form a linear pair.
Consider the angles ∠URP and ∠URX
Consider the angles ∠SVQ and ∠SVY
The angles ∠URP and ∠URX are supplementary
The angles ∠SVQ and ∠SVY are supplementary
Consider the angles ∠URX and ∠SVY
∠URX ≅ ∠SVY
Consider the triangles ΔURX and ΔSVY
∠URX ≅ ∠SVY
RU ≅ VS
∠XUR ≅ ∠YSV
ΔURX ≅ ΔSVY
Consider the triangles ΔPRU and ΔQVS
Consider the triangles ΔURX and ΔSVY
∠X ≅ ∠Y
∠P ≅ ∠Q
PU ≅ SQ
Consider the triangles ΔPUX and ΔQSY
∠X ≅ ∠Y
∠P ≅ ∠Q
PU ≅ SQ
ΔPUX ≅ ΔQSY
Question 17.
MODELING WITH MATHEMATICS
Explain how to find the distance across the canyon.
Answer:

Question 18.
HOW DO YOU SEE IT?
Use the tangram puzzle.
Answer:

a. Which triangle(s) have an area that is twice the area of the purple triangle?
b. How many times greater is the area of the orange triangle than the area of the purple triangle?
Answer:
The area of the orange triangle is 4 times greater than the area of the purple triangle in the tangram puzzle.
Question 19.
PROOF
Prove that the green triangles in the Jamaican flag congruent if \(\overline{A D}\) || \(\overline{B C}\) and E is the midpoint of \(\overline{A C}\).

Answer:


Question 20.
THOUGHT PROVOKING
The Bermuda Triangle is a region in the Atlantic Ocean in which many ships and planes have mysteriously disappeared. The vertices are Miami. San Juan. and Bermuda. Use the Internet or some other resource to find the side lengths. the perimeter, and the area of this triangle (in miles). Then create a congruent triangle on land using cities as vertices.
Answer:
Question 21.
MAKING AN ARGUMENT
Your friend claims that ∆WZY can be proven congruent to ∆YXW using the HL Congruence Theorem (Thm. 5.9). Is your friend correct? Explain your reasoning.
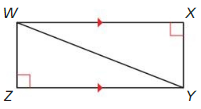
Answer:

Question 22.
CRITICAL THINKING
Determine whether each conditional statement is true or false. If the statement is false, rewrite it as a true statement using the converse, inverse, or contrapositive.
a. If two triangles have the same perimeter, then they are congruent.
b. If two triangles are congruent. then they have the same area.
Answer:
a. The statement is false
If two triangles are congruent, then they have the same perimeter.
b. The statement is true.
Question 23.
ATTENDING TO PRECISION
Which triangles are congruent to ∆ABC? Select all that apply.
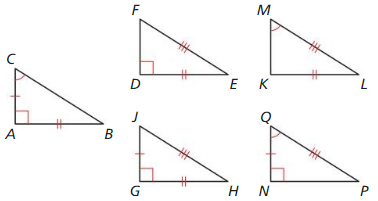
Answer:
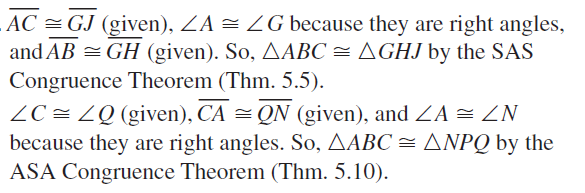
Maintaining Mathematical Proficiency
Find the perimeter of the polygon with the given vertices.
Question 24.
A(- 1, 1), B(4, 1), C(4, – 2), D(- 1, – 2)
Answer:
AB = √(4 + 1)² + (1 – 1)² = √5² + 0² = 5
BC = √(4 – 4)² + (-2 – 1)² = √0² + (-3)² = 3
CD = √(-1 – 4)² + (-2 + 2)² = √(-5)² + 0² = 5
AD = √(-1 + 1)² + (-2 – 1)² = √0² + (-3)² = 3
Perimeter of the polygon = AB + BC + CD + AD = 5 + 3 + 5 + 3 = 16
Question 25.
J(- 5, 3), K(- 2, 1), L(3, 4)
Answer:
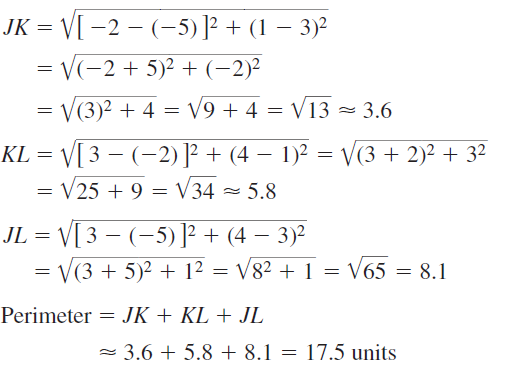
5.8 Coordinate Proofs
Exploration 1
Writing a coordinate Proof
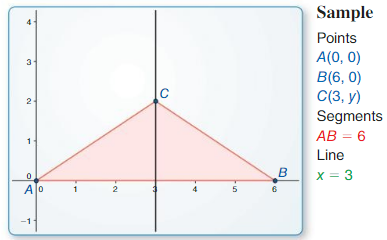
Work with a partner.
a. Use dynamic geometry software to draw \(\overline{A B}\) with endpoints A(0, 0) and B(6, 0).
Answer:
b. Draw the vertical line x = 3.
Answer:
c. Draw ∆ABC so that C lies on the line x = 3.
Answer:
d. Use your drawing to prove that ∆ABC is an isosceles triangle.
Answer:
Exploration 2
Writing a Coordinate proof
Work with a partner.
a. Use dynamic geometry software to draw \(\overline{A B}\) with endpoints A(0, 0) and B(6, 0).
b. Draw the vertical line x = 3.
c. Plot the point C(3, 3) and draw ∆ABC. Then use your drawing to prove that ∆ABC is an isosceles right triangle.
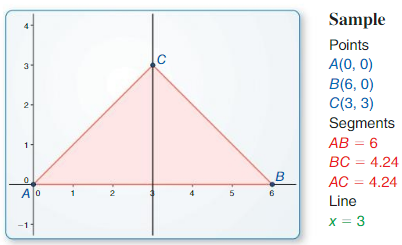
d. Change the coordinates of C so that C lies below the x-axis and ∆ABC is an isosceles right triangle.
Answer:
e. Write a coordinate proof to show that if C lies on the line x = 3 and ∆ABC is an isosceles right triangle. then C must be the point (3, 3) or the point found in part (d).
CRITIQUING THE REASONING OF OTHERS
To be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results.
Answer:
Communicate Your Answer
Question 3.
How can you use a coordinate plane to write a proof?
Answer:
A coordinate plane can be used to write a geometric proof by using generalized points on the plane and creating arguments.
In this method, variables are assigned to the coordinates of different points and then these coordinates are used in distance or midpoint formulas.
The coordinates of the points already present in the coordinate plane is also used for convenience in proving the theorems.
Making assumptions that a vertex is at its origin (if not given), or a side is lying on either of the axes makes it easier to move forward while we try to prove something.
Question 4.
Write a coordinate proof to prove that ∆ABC with vertices A(0, 0), 8(6, 0), and C(3, 3√3) is an equilateral triangle.
Answer:
Lesson 5.8 Coordinate Proofs
Monitoring Progress
Question 1.
Show another way to place the rectangle in Example 1 part (a) that is convenient
for finding side lengths. Assign new coordinates.
Answer:
Mark the points so that it is easy to find the distance between vertices.
The new coordinates are A(1, 1), B (5, 1), C (5, 4), D (1, 4)
Question 2.
A square has vertices (0, 0), (m, 0), and (0, m), Find the fourth vertex.
Answer:
By drawing the square on a graph. We can find the fourth vertex.
The fourth vertex is (m, m)
Question 3.
Write a plan for the proof.
Given \(\vec{G}\)J bisects ∠OGH.
Proof ∆GJO ≅ ∆GJH
Answer:
GJ ≅ GJ by the reflexive property of congruence
OG = √(3 – 0)² + (7 – 0)² = √9 + 49 = √58
GH = √(6 – 3)² + (0 – 7)² = √9 + 49 = √58
OG ≅ GH
OJ = √(3 – 0)² + (2 – 0)² = √9 + 4 = √13
JH = √(3 – 6)² + (2 – 0)² = √9 + 4 = √13
OJ ≅ JH
∆GJO ≅ ∆GJH by SAS congruence theorem.
Question 4.
Graph the points 0(0, 0), H(m, n), and J(m, 0). Is ∆OHJ a right triangle? Find the side lengths and the coordinates of the midpoint of each side.
Answer:
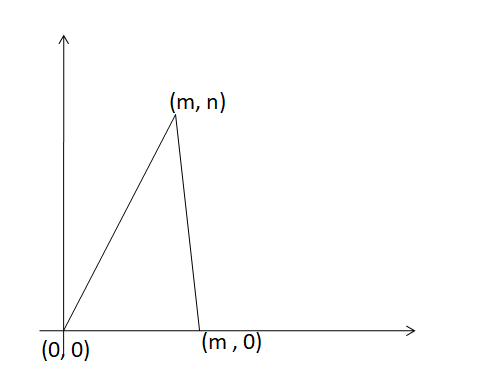
Side lengths are OA = √(m – 0)² + (n – 0)² = √m² + n²
OB = √(m – 0)² + (0 – 0)² = √m² = m
AB = √(m – m)² + (n – 0)² = √n² = n
By using the Pythagorean theorem,
OA² = OB² + AB²
m² + n² = m² + n²
So, the trinagle is a right-angled triangle.
Question 5.
Write a coordinate proof.
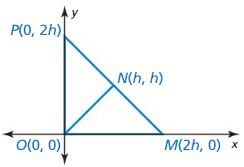
Given Coordinates of vertices of ∆NPO and ∆NMO
Prove ∆NPO ≅ ∆NMO
Answer:
NP = √(h – 0)² + (h – 2h)² = √h² + h² = h√2
OP = √(0 – 0)² + (0 – 2h)² = √4h² = 2h
ON = √(0 – h)² + (0 – h)² = √h² + h² = h√2
NM = √(h – 2h)² + (h – 0)² = √h² + h² = h√2
ON = √(0 – h)² + (0 – h)² = √h² + h² = h√2
OM = √(2h – 0)² + (0 – 0)² = √4h² = 2h
NP ≅ NM, OP ≅ OM, ON ≅ ON
So, ∆NPO ≅ ∆NMO by SSS congruence theorem
Exercise 5.8 Coordinate Proofs
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
How is a coordinate proof different from other types of proofs you have studied?
How is it the same?
Answer:

Question 2.
WRITING
Explain why it is convenient to place a right triangle on the grid as shown when writing a coordinate proof.
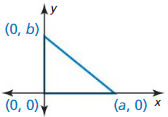
Answer:
Because the right triangle has the base and another leg on the same line in the coordinate plane.
Maintaining Progress and Modeling with Mathematics
In Exercises 3-6, place (he figure in a coordinate plane in a convenient way. Assign coordinates to each vertex. Explain the advantages of your placement.
Question 3.
a right triangle with leg lengths of 3 units and 2 units
Answer:
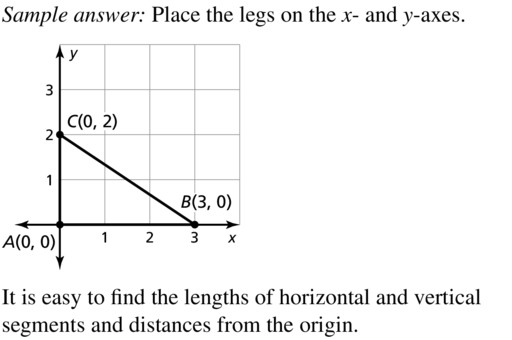
Question 4.
a square with a side length of 3 units
Answer:
Place the sides on the x-axis, y-axis
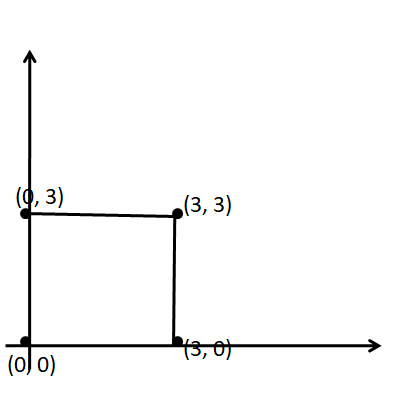
It is easy to find the lengths of horizontal and vertical segments and distances from the origin.
Question 5.
an isosceles right triangle with leg length p
Answer:
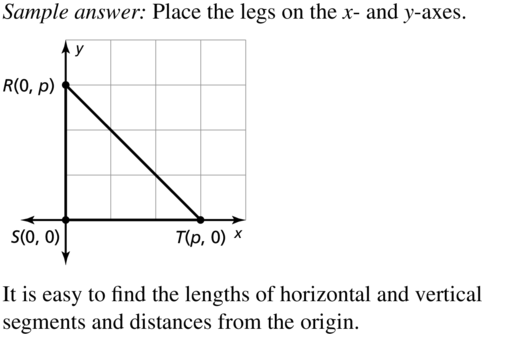
Question 6.
a scalene triangle with one side length of 2m
Answer:
In Exercises 7 and 8, write a plan for the proof.
Question 7.
Given Coordinates of vertices of ∆OPM and ∆ONM Prove ∆OPM and ∆ONM are isosceles triangles.
Answer:
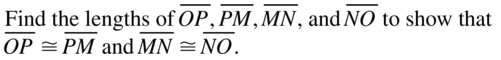
Question 8.
Given G is the midpoint of \(\overline{H F}\).
Prove ∆GHJ ≅ ∆GFO
Answer:
The coordinates of G are (3, 2)
OG = √(3 – 0)² + (2 – 0)² = √9 + 4 = √13
OF = √(5 – 0)² + (0 – 0)² = 5
GF = √(5 – 3)² + (0 – 2)² = √2² + 2² = √8
GH = √(3 – 1)² + (2 – 4)² = √2² + 2² = √8
HJ = √(6 – 1)² + (4 – 4)² = √5² = 5
GJ = √(6 – 3)² + (4 – 2)² = √9 + 4 = √13
OG ≅ GJ, OF ≅ HJ, GF ≅ GH
So, ∆GHJ ≅ ∆GFO by SSS congruence theorem.
In Exercises 9-12, place the figure in a coordinate plane and find the indicated length.
Question 9.
a right triangle with leg lengths of 7 and 9 units; Find the length of the hypotenuse.
Answer:
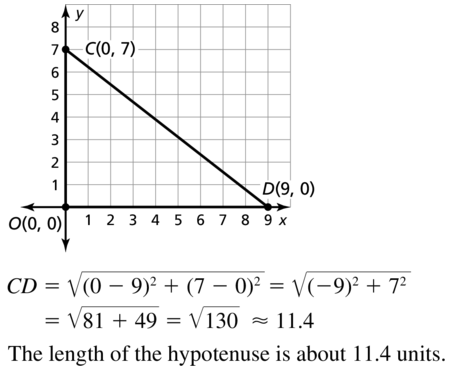
Question 10.
an isosceles triangle with a base length of 60 units and a height of 50 units: Find the length of one of the legs.
Answer:
The coordinates of the vertices A(0, 0), B(60, 0), C(30, 50)
The length of one leg AC = √(50 – 0)² + (30 – 0)² = √2500 + 900 = √3400 = 58.31
Question 11.
a rectangle with a length o! 5 units and a width of 4 units: Find the length of the diagonal.
Answer:
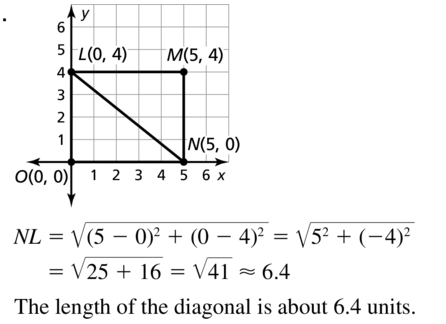
Question 12.
a square with side length n: Find the length of the diagonal.
Answer:
The length of diagonal = √(n – 0)² + (n – 0)² = √n² + n² = n√2
In Exercises 13 and 14, graph the triangle with the given vertices. Find the length and the slope of each side of the triangle. Then find the coordinates of the midpoint of each side. Is the triangle a right triangle? isosceles? Explain. Assume all variables are positive and in m ≠ n.)
Question 13.
A(0, 0), B(h, h), C(2h, 0)
Answer:
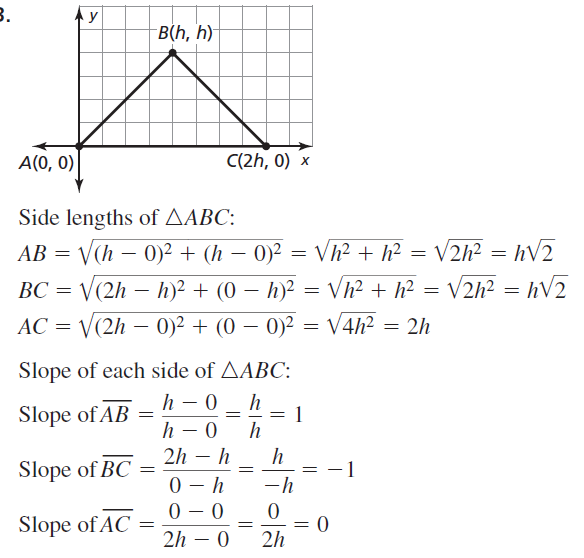
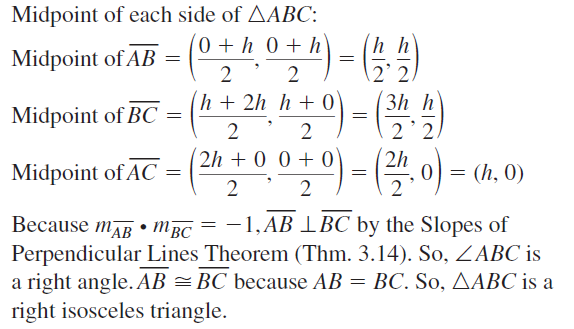
Question 14.
D(0, n), E(m, n), F(m, 0)
Answer:
Side lengths of △DEF
DE = √(m – 0)² + (n – n)² = m
EF = √(m – m)² + (0 – n)² = n
DF = √(m – 0)² + (0 – n)² = √m² + n²
Slopes of △DEF
Slope of DE = \(\frac { n – n }{ n – 0 } \) = 0
Slope of EF = \(\frac { 0 – n }{ m – m } \) = undefined
Slope of DF = \(\frac { m – 0 }{ 0 – n } \) = \(\frac { -m }{ n } \)
Midpoint of DE = (\(\frac { 0 + m }{ 2 } \), \(\frac { n + n }{ 2 } \)) = (\(\frac { m }{ 2 } \), n)
Midpoint of EF = (\(\frac { m + m }{ 2 } \), \(\frac { n + 0 }{ 2 } \)) = (m, \(\frac { n }{ 2 } \))
Midpoint of DF = (\(\frac { 0 + m }{ 2 } \), \(\frac { n + 0 }{ 2 } \)) = (\(\frac { m }{ 2 } \), \(\frac { n }{ 2 } \))
In Exercises 15 and 16, find the coordinates of any unlabeled vertices. Then find the indicated length(s).
Question 15.
Find ON and MN.
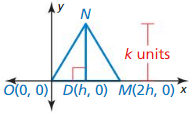
Answer:
Question 16.
Find OT.
Answer:
OT = √(2k – 0)² + (2k – 0)²
= √(2k)² + (2k)²
= √8k²
= 2k√2 units
PROOF
In Exercises 17 and 18, rite a coordinate proof.
Question 17.
Given Coordinates of vertices of ∆DEC and ∆BOC
Prove ∆DEC ≅ ∆BOC
Answer:

Question 18.
Given Coordinates of ∆DEA, H is the midpoint of \(\overline{D A}\), G is the mid point of \(\overline{E A}\)
Prove \(\overline{D G}\) ≅ \(\overline{E H}\)
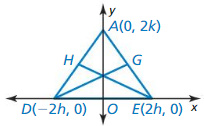
Answer:
G is the mid point of \(\overline{E A}\)
So, G = (\(\frac { 2h + 0 }{ 2 } \), \(\frac { 0 + 2k }{ 2 } \)) = (h, k)
H is the midpoint of \(\overline{D A}\)
So, H = (\(\frac { -2h + 0 }{ 2 } \), \(\frac { 2k + 0 }{ 2 } \)) = (-h, k)
\(\overline{D G}\) = √(h + 2h)² + (k – 0)² = √9h² + k²
\(\overline{E H}\) = √(-h – 2h)² + (0 – k)² = √9h² + k²
Question 19.
MODELING WITH MATHEMATICS
You and your cousin are camping in the woods. You hike to a point that is 500 meters cast and 1200 meters north of the Campsite. Your cousin hikes to a point that is 1000 meters cast of the campsite. Use a coordinate proof to prove that the triangle formed by your Position, your Cousin’s position. and the campsite is isosceles. (See Example 5.)

Answer:
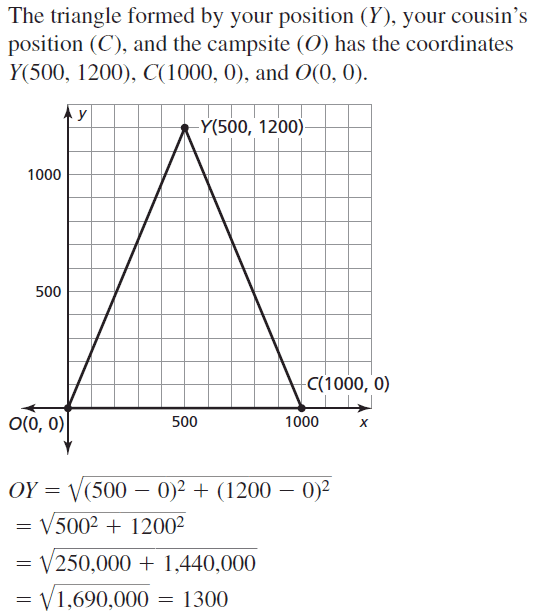

Question 20.
MAKING AN ARGUMENT
Two friends see a drawing of quadrilateral PQRS with vertices P(0, 2), Q(3, – 4), R(1, – 5), and S(- 2, 1). One friend says the quadrilateral is a parallelogram but not a rectangle. The other friend says the quadrilateral is a rectangle. Which friend is correct? Use a coordinate proof to support your answer.
Answer:
It can be seen that PS || QR and PQ || SR. If PQRS is a rectangle then PS ⊥ PQ, therefore find slopes of PS and PQ.
Slope of PS = \(\frac { 1 – 2 }{ -2 – 0 } \) = \(\frac { 1 }{ 2 } \)
Slope of PQ = \(\frac { -4 – 2 }{ 3 – 0 } \) = -2
It can be seen that slope of PS is negative reciprocal of slope of PQ.
So, PS is perpendicular to PQ and PQRS is a rectangle.
Question 21.
MATHEMATICAL CONNECTIONS
Write an algebraic expression for the coordinates of each endpoint of a line segment whose midpoint is the origin.
Answer:
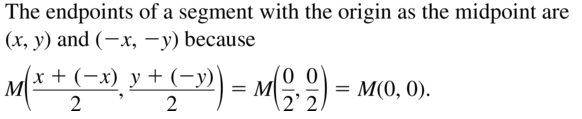
Question 22.
REASONING
The vertices of a parallelogram are (w, 0), (0, v), (- w, 0), and (0, – v). What is the midpoint of the side in Quadrant III?
(a) \(\left(\frac{w}{2}, \frac{v}{2}\right)\)
(b) \(\left(-\frac{w}{2},-\frac{v}{2}\right)\)
(c) \(\left(-\frac{w}{2}, \frac{v}{2}\right)\)
(d) \(\left(\frac{w}{2},-\frac{v}{2}\right)\)
Answer:
The midpoint of the side in Quadrant III = (\(\frac { -w + 0 }{ 2 } \), \(\frac { 0 – v }{ 2 } \))
= (\(\frac { -w }{ 2 } \), \(\frac { -v }{ 2 } \))
Question 23.
REASONING
A rectangle with a length of 3h and a width of k has a vertex at (- h, k), Which point cannot be a vertex of the rectangle?
(A) (h, k)
(B) (- h, 0)
(c) (2h, 0)
(D) (2h, k)
Answer:
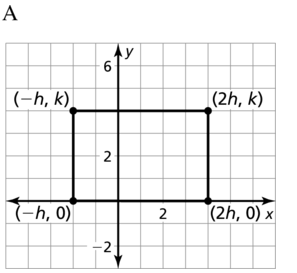
Question 24.
THOUGHT PROVOKING
Choose one of the theorems you have encountered up to this point that you think would be easier to prove with a coordinate proof than with another type of proof. Explain your reasoning. Then write a coordinate proof.
Answer:
A(-h, 0), B(0, k) and C(h, 0)
Slope of BC = 0 – k/h – 0 = -k/h
The slope of AC = k-0/0-(-h) = k/h
Slope of BC = – slope of AC
If the slopes are equal in magnitude but opposite in direction, then the sides are equal in length.
∠BCA ≅ ∠BAC
If two sides of a triangle are congruent, then the angles opposite to them are congruent.
Question 25.
CRITICAL THINKING
The coordinates of a triangle are (5d – 5d), (0, – 5d), and (5d, 0). How sh
would the coordinates be changed to make a coordinate proof easier to complete?
Answer:
Question 26.
HOW DO YOU SEE IT?
without performing any calculations, how do you know that the diagonals of square TUVW are perpendicular to each oilier? How can you use a similar diagram to show that the diagonals of any square are perpendicular to each other?
Answer:
As the vertices are in the opposite sign, the diagonals of square TUVW are perpendicular to each other.
Question 27.
PROOF
Write a coordinate proof for each statement.
a. The midpoint o! the hypotenuse of a right triangle is the same distance from each vertex of the triangle.
b. Any two congruent right isosceles triangles can be combined to form a single isosceles triangle.
Answer:
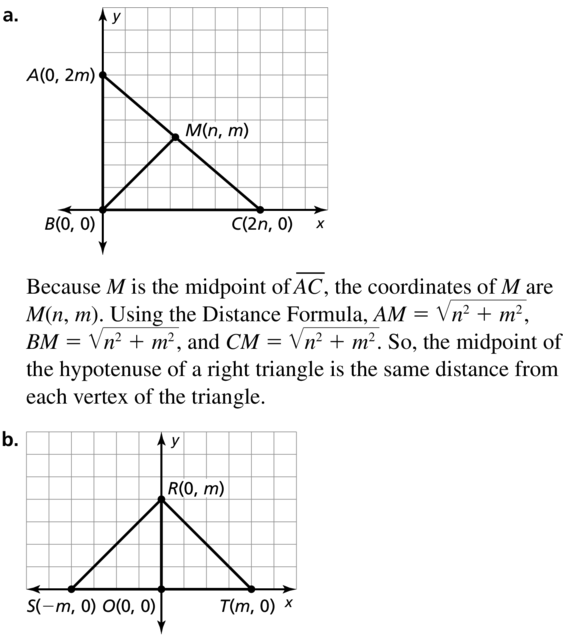

Maintaining Mathematical proficiency
\(\vec{Y}\)W bisects ∠XYZ such that m∠XYW = (3x – 7)° and m∠WYZ = (2x + 1)°.
Question 28.
Find the value of x.
Answer:
(3x – 7)° = (2x + 1)
3x – 2x = 1 + 7
x = 8
Question 29.
Find m∠XYZ
Answer:
Congruent Triangles Chapter Review
5.1 Angles of Triangles
Question 1.
Classify the triangle at the right by its sides and by measuring its angles.
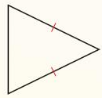
Answer:
The triangle have two congruent sides. So, the triangle is an isosceles triangle.
Therefore, the measure of angles is less than 90 degrees. So these are obtuse angles.
Find the measure of the exterior angle.
Question 2.
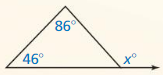
Answer:
Sum of angles = 180
46 + 86 + y = 180
y = 48
x° = 180° – 48° = 132°
Question 3.
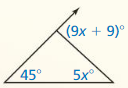
Answer:
y = 180 – (9x + 9)
Sum of interior angles = 180
45 + 5x + y = 180
45 + 5x + 180 – (9x + 9) = 180
45 – 4x – 9 = 0
4x = 36
x = 9
Find the measure of each acute angle.
Question 4.
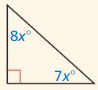
Answer:
Sum of interior angles = 180
90 + 8x + 7x = 180
15x = 90
x = 6
Question 5.
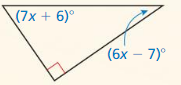
Answer:
Sum of interior angles = 180
7x + 6 + 90 + 6x – 7 = 180
13x – 1 = 90
13x = 91
x = 7
5.2 Congruent Polygons
Question 6.
In the diagram. GHJK ≅ LMNP. Identify all pairs of congruent corresponding parts. Then write another congruence statement for the quadrilaterals.
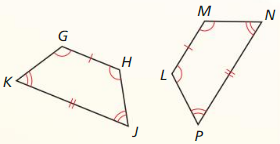
Answer:
Corresponding sides: GH ≅ LM, KJ ≅ PN
Corresponding angles: ∠G ≅ ∠H ≅ ∠L ≅ ∠M, ∠K ≅ ∠J ≅ ∠P ≅ ∠N
Question 7.
Find m ∠ V.
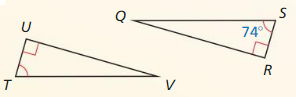
Answer:
∠T ≅ ∠S
Sum of interior angles = 180
90 + 74 + m ∠ V =180
164 + m ∠ V = 180
m ∠ V = 16
5.3 Proving Triangle Congruence by SAS
Decide whether enough information is given to prove that ∆WXZ ≅ ∆YZX using the SAS Congruence Theorem (Theorem 5.5). If so, write a proof. If not, explain why.
Question 8.
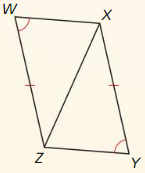
Answer:
∠W ≅ ∠Y
WZ ≅ XY
XZ ≅ XZ by the reflexive property of congruence
△ XZW ≅ △XYZ by SAS Congruence Theorem
Question 9.
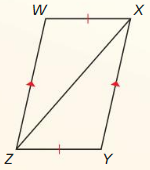
Answer:
WX ≅ ZY
WZ ≅ XY
XZ ≅ XZ by the reflexive property of congruence
△ XZW ≅ △XYZ by SAS Congruence Theorem
5.4 Equilateral and Isosceles Triangles
Copy and Complete the statement.
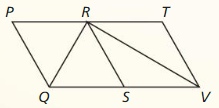
Question 10.
If \(\overline{Q P}\) ≅ \(\overline{Q R}\), then ∠ ______ ≅ ∠ ______ .
Answer:
If \(\overline{Q P}\) ≅ \(\overline{Q R}\), then ∠ P ≅ ∠ R
Question 11.
If ∠TRV ≅ ∠TVR, then ______ ≅ ______ .
Answer:
If ∠TRV ≅ ∠TVR, then TR ≅ TV
Question 12.
If \(\overline{R Q} \cong \overline{R S}\), then ∠ ______ ≅ ∠ ______ .
Answer:
If \(\overline{R Q} \cong \overline{R S}\), then ∠ Q ≅ ∠ S .
Question 13.
If ∠SRV ≅ ∠SVR, then ______ ≅ ______ .
Answer:
If ∠SRV ≅ ∠SVR, then SR ≅ VR .
Question 14.
Find the values of x and y in the diagram.
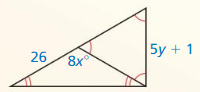
Answer:
5.5 Proving Triangle Congruence by SSS
Question 15.
Decide whether enough information is given to prove that ∆LMP ≅ ∆NPM using the SSS Congruence Theorem (Thin. 5.8). If so, write a proof. If not, explain why.
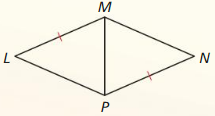
Answer:
LM ≅ NP, MP ≅ MP by reflexive property of congruence.
We need one more side to be congruent to prove that ∆LMP ≅ ∆NPM using the SSS Congruence Theorem
Question 16.
Decide whether enough information is given to prove that ∆WXZ ≅ ∆YZX using the HL Congruence Theorem (Thm. 5.9). If so, write a proof. If not, explain why.
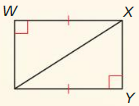
Answer:
XZ ≅ XZ by reflexive property of congruence.
The hypotenuse leg of ∆WXZ and ∆YZX are congruent.
So, ∆WXZ ≅ ∆YZX
5.6 Proving Triangle Congruence by ASA and AAS
Question 17.
∆EFG, ∆HJK
Answer:
∠E ≅ ∠H, ∠F ≅ ∠J, FG ≅ KJ
So, ∆EFG ≅ ∆HJK by AAS Congruence Theorem.
Question 18.
∆TUS, ∆QRS
Answer:
∠T ≅ ∠Q, TU ≅ QR
The given information is not enough to prove that ∆TUS ≅ ∆QRS using AASCongruence Theorem.
Decide whether enough information is given to prove that the triangles are congruent using the ASA Congruence Theorem (Thm. 5.10). If so, write a proof, If not, explain why.
Question 19.
∆LPN, ∆LMN
Answer:
∠PNL ≅ ∠MNL, ∠PLN ≅ ∠MLN
LN ≅ LN by reflexive property of congruence
So, ∆LPN ≅ ∆LMN using ASA Congruence Theorem.
Question 20.
∆WXZ, ∆YZX
Answer:
WZ ≅ XY
XZ ≅ XZ by reflexive property of congruence theorem
So, the given information is not enough to prove that ∆WXZ ≅ ∆YZX using ASA Congruence Theorem.
5.7 Using Congruent Triangles
Question 21.
Explain how to prove that ∠K ≅∠N.
Answer:
HJ ≅ ML
KJ ≅ NM
∠J ≅ ∠M
So, ∆HKJ ≅ ∆MNL using SAS congruence theorem.
∠K ≅∠N
Question 22.
Write a plan to prove that ∠1 ≅ ∠2
Answer:
Given ∆QSV, ∆QVT, ∆PUS, ∆RTV
SV ≅ QT, SV ≅ VT
∠1 ≅ ∠2
∠QSV ≅ ∠QTV
∠QSV and ∠1 (vertically opposite angles)
∠QTV and ∠2 (vertically opposite angles)
5.8 Coordinate Proofs
Question 23.
Write a coordinate proof.
Given Coordinates of vertices of quadrilateral OPQR
Prove ∆OPQ ≅ ∆QRO
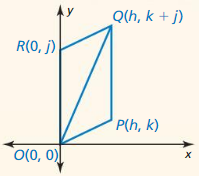
Answer:
OP = √(h – 0)² + (k – 0)² = √h² + k²
OQ = √(h -0)² + (k + j – 0 )² = √h² + (k + j)²
PQ = √(h – h)² + (k – k – j)² = √0² + j² = j
OR = √(0 – 0)² + (0 – j)² = √j² = j
OQ = √(h – 0)² + (k + j – 0)² = √h² + (k + j)²
QR = √(h – 0)² + (k + j – j)² = √h² + k²
OP ≅ QR, OQ ≅ OQ, PQ ≅ OR
So, ∆OPQ ≅ ∆QRO using SSS Congruence Theorem.
Question 24.
Place an isosceles triangle in a coordinate plane in a way that is convenient for finding side lengths. Assign coordinates to each vertex.
Answer:
Question 25.
A rectangle has vertices (0, 0), (2k, 0), and (0, k), Find the fourth vertex.
Answer:
From the image, the fourth vertex is (2k, k).
Congruent Triangles Test
Write a Proof.
Question 1.
Given \(\overline{C A} \cong \overline{C B} \cong \overline{C D} \cong \overline{C E}\)
Prove ∆ABC ≅ ∆EDC
Answer:
Given \(\overline{C A} \cong \overline{C B} \cong \overline{C D} \cong \overline{C E}\)
As ∆ABC and ∆EDC are isosceles triangles.
So, ∆ABC ≅ ∆EDC
Question 2.
Given \(\overline{J K}\|\overline{M L}, \overline{M J}\| \overline{K L}\)
Prove ∆MJK ≅ ∆KLM
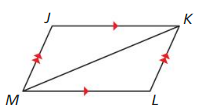
Answer:
\(\overline{J K}\|\overline{M L}, \overline{M J}\| \overline{K L}\)
MK ≅ MK by reflexive property of congruence
So, ∆MJK ≅ ∆KLM using SSS congruence theorem.
Question 3.
Given \overline{Q R} \cong \overrightarrow{R S}\(\), ∠P ≅ ∠T
Prove ∆SRP ≅ ∆QRT
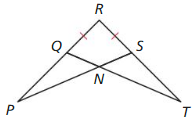
Answer:
QR ≅ RS, ∠P ≅ ∠T
∠R ≅ ∠R by reflexive property of congruence
So, ∆SRP ≅ ∆QRT using AAS Congruence Theorem
Question 4.
Find the measure of each acute angle in the figure at the right.
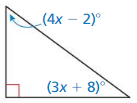
Answer:
90 + 4x – 2 + 3x + 8 = 180
96 + 7x = 180
7x = 180 – 96
7x = 84
x = 12
Question 5.
Is it possible to draw an equilateral triangle that is not equiangular? If so, provide an example. If not, explain why.
Answer:
All equilateral triangles will be equiangular
Question 6.
Can you use the Third Angles Theorem (Theorem 5.4) to prove that two triangles are congruent? Explain your reasoning.
Answer:
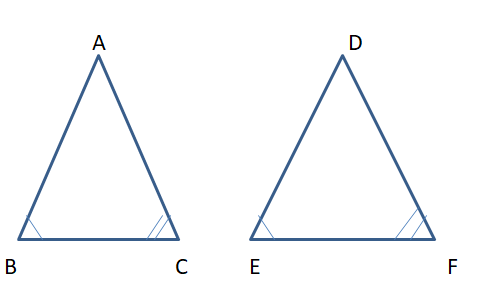
∠B ≅ ∠E, ∠C ≅ ∠F
Then ∠A ≅ ∠D using third angles theorem.
Write a plan through that ∠1 ≅∠2
Question 7.
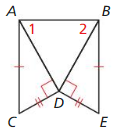
Answer:
Question 8.
Answer:
Question 9.
Is there more than one theorem that could be used to prove that ∆ABD ≅ ∆CDB? If so, list all possible theorems.
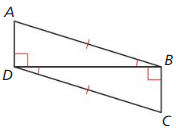
Answer:
The first theorem is HL Congruence Theorem
AB ≅ CD
The second theorem is SAS Congruence Theorem
AB ≅ CD
DB ≅ DB by reflexive property of congruence
∠D ≅ ∠B
Question 10.
Write a coordinate proof to show that the triangles created b the keyboard stand are congruent.
Answer:
The coordinates of T(3, 0), S(21, 0), R (12, 15), P(3, 30), Q(21, 30)
PQ = √(21 – 3)² + (30 – 30)² = 18
PR = √(3 – 12)² + (30 – 15)² = √9² + 15² = √306
RQ = √(21 – 12)² + (30 – 15)² = √9² + 15² = √306
TR = √(12 – 3)² + (15 – 0)² = √9² + 15² = √306
TS = √(21 – 3)² + (0 – 0)² = √18² = 18
RS = √(21 – 12)² + (0 – 15)² = √9² + 15² = √306
PQ ≅ TS, PR ≅ TR, RQ ≅ RS
So, △PQR ≅ △TRS using SSS congruence theorem
Question 11.
The picture shows the Pyramid of Cestius. which is located in Rome, Italy. The measure of the base for the triangle shown is 100 Roman feet. The measures of the other two sides of the triangle are both 144 Roman feet.

a. Classify the triangle shown by its sides.
Answer:
The triangle is an isosceles triangle.
b. The measure of ∠3 is 40° What are the measures of ∠1 and ∠2? Explain your reasoning.
Answer:
∠3 + 2x = 180
40 + 2x = 180
2x = 140
x = 70
Congruent Triangles Cumulative Assessment
Question 1.
Your friend claims that the Exterior Angle Theorem (Theorem 5.2) can be used to prove the Triangle Sum Theorem (Theorem 5, 1). Is your friend correct? Explain your reasoning.
Answer:
Yes
Question 2.
Use the steps in the construction to explain how you know that the line through point P is parallel to line m.
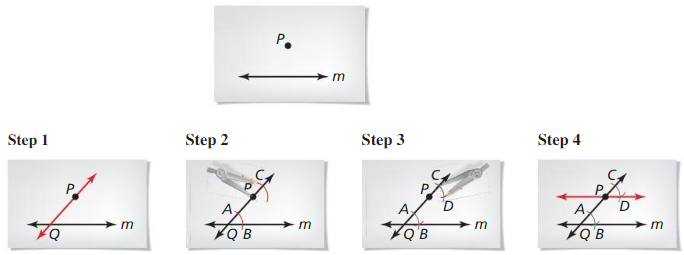
Answer:
From step 4 the red line is parallel to m and passes through the pint P. So, point P is parallel to line m.
Question 3.
The coordinate plane shows ∆JKL and ∆XYZ
a. Write a composition of transformations that maps ∆JKL to ∆XYZ
Answer:
The coordinates of J(-3, 2), L (0, 2) K(-2, 4), X(1, -2), Y(2, -4), Z(4, -2)
JL = √(0 + 3)² + (2 – 2)² = 3
XZ = √(4 – 1)² + (-2 + 2)² = 3
JK = √(-2 + 3)² + (4 – 2)² = √5
XY = √(2 – 1)² + (-4 + 2)² = √5
KL = √(-2 – 0)² + (4 – 2)² = √8
YZ = √(4 – 2)² + (-2 + 4)²= √8
JK ≅ XY, JL ≅ XZ, KL ≅ YZ
b. Is the composition a congruence transformation? If so, identify all congruent corresponding parts.
Answer:
△JKL ≅ △XYZ using the SSS Congruence theorem.
Question 4.
The directed line segment RS is shown. Point Q is located along \(\overline{R S}\) so that the ratio of RQ to QS is 2 to 3. What are the coordinates of point Q?
(A) Q(1.2, 3)
(B) Q(4, 2)
(C) Q(2, 3)
(D) Q(-6, 7)
Answer:
RQ : RS = 2 : 3
The coordinates of R(-2, 5), S(8, 0)
Let us validate answer with Q(2, 3)
RQ = √(2 + 2)² + (3 – 5)² = √16 + 4 = √20 = 4.47
RS = √(8 + 2)² + (0 – 5)² = √125 = 11.18
If Q(4, 2)
RQ = √(4 + 2)² + (2 – 5)² = √45
Now, RQ : RS = 2 : 3
So, Q(4, 2)
Question 5.
The coordinate plane shows that ∆ABC and ∆DEF
a. Prove ∆ABC ≅ ∆DEF using the given information.
Answer:
∠B ≅ ∠E, BC ≅ EF
So, ∆ABC ≅ ∆DEF
b. Describe the composition of rigid motions that maps ∆ABC to ∆DEF
Answer:
Question 6.
The vertices of a quadrilateral are W(0, 0), X(- 1, 3), )(2, 7), and Z(4, 2). Your friend claims that point W will not change after dilatinig quadrilateral WXYZ by a scale factor of 2. Is your friend correct? Explain your reasoning.
Answer:
Question 7.
Which figure(s) have rotational symmetry? Select all that apply.
(A) 
(B) 
(C) 
(D) 
Answer:
(D)
Because by rotating the symbol, we get the same image.
Question 8.
Write a coordinate proof.
Given Coordinates of vertices of quadrilateral ABCD
Prove Quadrilateral ABCD is a rectangle.
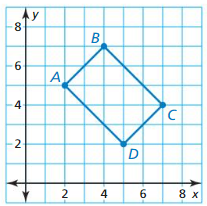
Answer:
The vertices of A(2, 5), B(4, 7), C(7, 4), D(5, 2)
The slope of AB = \(\frac { 4 – 2 }{ 7 – 5 } \) = \(\frac { 2 }{ 2 } \) = 1
The slope of AD = \(\frac { 5 – 2 }{ 2 – 5 } \) = \(\frac { 3 }{ -3 } \) = -1
The slope of AB and AD are negative reciprocals
So, AB is perpendicular to AD
So, ABCD is a rectangle.
Question 9.
Write a proof to verify that the construction of the equilateral triangle shown below is valid.
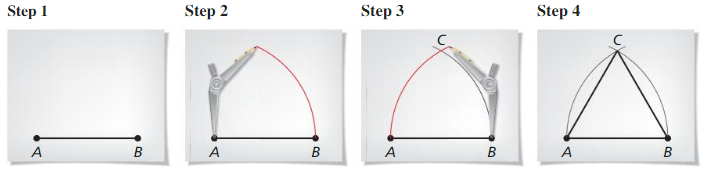
Answer:
At step 1, we need to draw the base AB
With A as centre and AB as radius draw an arc and with B as centre and AB as radius draw another arc intersecting the first arc at C.
Name that point as C. Now formed triangle ABC is an equilateral triangle.
