Engage NY Eureka Math 5th Grade Module 5 Lesson 7 Answer Key
Eureka Math Grade 5 Module 5 Lesson 7 Sprint Answer Key
A
Multiply Fractions

Question 1.
\(\frac{1}{2}\) × \(\frac{1}{2}\) =
Answer: 1/4
Question 2.
\(\frac{1}{2}\) × \(\frac{1}{3}\) =
Answer: 1/6
Question 3.
\(\frac{1}{2}\) × \(\frac{1}{4}\) =
Answer: 1/8
Question 4.
\(\frac{1}{2}\) × \(\frac{1}{7}\) =
Answer: 1/14
Question 5.
\(\frac{1}{7}\) × \(\frac{1}{2}\) =
Answer: 1/14
Question 6.
\(\frac{1}{3}\) × \(\frac{1}{2}\) =
Answer: 1/6
Question 7.
\(\frac{1}{3}\) × \(\frac{1}{3}\) =
Answer: 1/9
Question 8.
\(\frac{1}{3}\) × \(\frac{1}{6}\) =
Answer: 1/18
Question 9.
\(\frac{1}{3}\) × \(\frac{1}{5}\) =
Answer: 1/15
Question 10.
\(\frac{1}{5}\) × \(\frac{1}{3}\) =
Answer: 1/15
Question 11.
\(\frac{1}{5}\) × \(\frac{2}{3}\) =
Answer: 2/15
Question 12.
\(\frac{2}{3}\) × \(\frac{2}{3}\) =
Answer: 4/9
Question 13.
\(\frac{1}{4}\) × \(\frac{1}{3}\) =
Answer: 1/12
Question 14.
\(\frac{1}{4}\) × \(\frac{2}{3}\) =
Answer: 2/12
Question 15.
\(\frac{3}{4}\) × \(\frac{2}{3}\) =
Answer: 6/12
Question 16.
\(\frac{1}{6}\) × \(\frac{1}{3}\) =
Answer: 1/18
Question 17.
\(\frac{5}{6}\) × \(\frac{1}{3}\) =
Answer: 5/18
Question 18.
\(\frac{5}{6}\) × \(\frac{2}{3}\) =
Answer: 10/18
Question 19.
\(\frac{5}{4}\) × \(\frac{2}{3}\) =
Answer: 10/12
Question 20.
\(\frac{1}{5}\) × \(\frac{1}{5}\) =
Answer: 1/25
Question 21.
\(\frac{2}{5}\) × \(\frac{2}{5}\) =
Answer: 4/25
Question 22.
\(\frac{2}{5}\) × \(\frac{3}{5}\) =
Answer: 6/25
Question 23.
\(\frac{2}{5}\) × \(\frac{5}{3}\) =
Answer: 10/15
Question 24.
\(\frac{3}{5}\) × \(\frac{5}{2}\) =
Answer: 15/10
Question 25.
\(\frac{1}{3}\) × \(\frac{1}{3}\) =
Answer: 1/9
Question 26.
\(\frac{1}{3}\) × \(\frac{2}{3}\) =
Answer: 2/9
Question 27.
\(\frac{2}{3}\) × \(\frac{2}{3}\) =
Answer: 4/9
Question 28.
\(\frac{2}{3}\) × \(\frac{3}{2}\) =
Answer: 6/6
Question 29.
\(\frac{2}{3}\) × \(\frac{4}{3}\) =
Answer: 8/9
Question 30.
\(\frac{2}{3}\) × \(\frac{5}{3}\) =
Answer: 10/9
Question 31.
\(\frac{3}{2}\) × \(\frac{3}{5}\) =
Answer: 9/10
Question 32.
\(\frac{3}{4}\) × \(\frac{1}{5}\) =
Answer: 3/20
Question 33.
\(\frac{3}{4}\) × \(\frac{4}{5}\) =
Answer: 12/20
Question 34.
\(\frac{3}{4}\) × \(\frac{5}{5}\) =
Answer: 15/20
Question 35.
\(\frac{3}{4}\) × \(\frac{6}{5}\) =
Answer: 18/20
Question 36.
\(\frac{1}{4}\) × \(\frac{6}{5}\) =
Answer: 6/20
Question 37.
\(\frac{1}{7}\) × \(\frac{1}{7}\) =
Answer: 1/49
Question 38.
\(\frac{1}{8}\) × \(\frac{3}{5}\) =
Answer: 3/40
Question 39.
\(\frac{5}{6}\) × \(\frac{1}{4}\) =
Answer: 5/24
Question 40.
\(\frac{3}{4}\) × \(\frac{3}{4}\) =
Answer: 9/16
Question 41.
\(\frac{2}{3}\) × \(\frac{6}{6}\) =
Answer: 12/18
Question 42.
\(\frac{3}{4}\) × \(\frac{6}{2}\) =
Answer: 18/8
Question 43.
\(\frac{7}{8}\) × \(\frac{7}{9}\) =
Answer: 49/72
Question 44.
\(\frac{7}{12}\) × \(\frac{9}{8}\) =
Answer: 63/96
B
Multiply Fractions
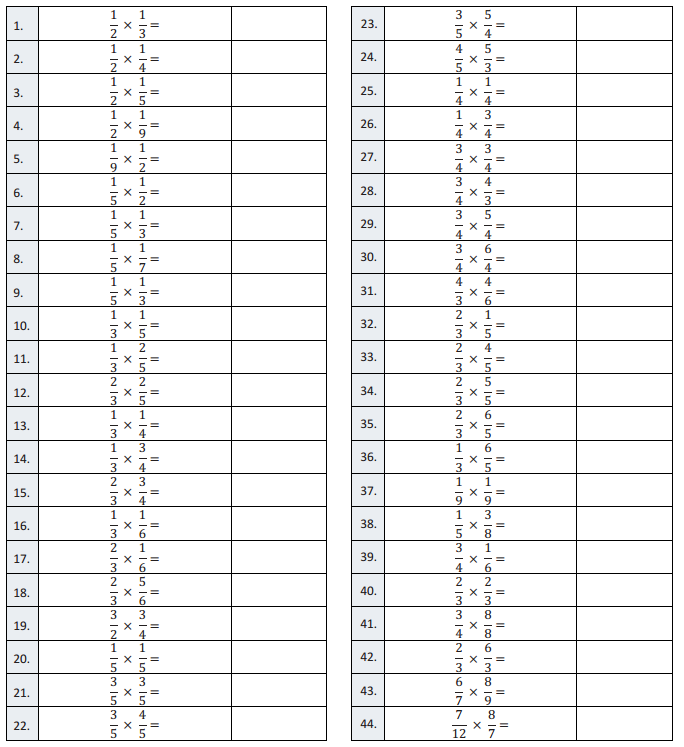
Question 1.
\(\frac{1}{2}\) × \(\frac{1}{3}\) =
Answer: 1/6
Question 2.
\(\frac{1}{2}\) × \(\frac{1}{4}\) =
Answer: 1/8
Question 3.
\(\frac{1}{2}\) × \(\frac{1}{5}\) =
Answer: 1/10
Question 4.
\(\frac{1}{2}\) × \(\frac{1}{9}\) =
Answer: 1/18
Question 5.
\(\frac{1}{9}\) × \(\frac{1}{2}\) =
Answer: 1/18
Question 6.
\(\frac{1}{5}\) × \(\frac{1}{2}\) =
Answer: 1/10
Question 7.
\(\frac{1}{5}\) × \(\frac{1}{3}\) =
Answer: 1/15
Question 8.
\(\frac{1}{5}\) × \(\frac{1}{7}\) =
Answer: 1/35
Question 9.
\(\frac{1}{5}\) × \(\frac{1}{3}\) =
Answer: 1/15
Question 10.
\(\frac{1}{3}\) × \(\frac{1}{5}\) =
Answer: 1/15
Question 11.
\(\frac{1}{3}\) × \(\frac{2}{5}\) =
Answer: 2/15
Question 12.
\(\frac{2}{3}\) × \(\frac{2}{5}\) =
Answer: 4/15
Question 13.
\(\frac{1}{3}\) × \(\frac{1}{4}\) =
Answer:1/12
Question 14.
\(\frac{1}{3}\) × \(\frac{3}{4}\) =
Answer: 3/12
Question 15.
\(\frac{2}{3}\) × \(\frac{3}{4}\) =
Answer: 6/12
Question 16.
\(\frac{1}{3}\) × \(\frac{1}{6}\) =
Answer: 1/18
Question 17.
\(\frac{2}{3}\) × \(\frac{1}{6}\) =
Answer: 2/18
Question 18.
\(\frac{2}{3}\) × \(\frac{5}{6}\) =
Answer: 10/18
Question 19.
\(\frac{3}{2}\) × \(\frac{3}{4}\) =
Answer: 9/8
Question 20.
\(\frac{1}{5}\) × \(\frac{1}{5}\) =
Answer: 1/25
Question 21.
\(\frac{3}{5}\) × \(\frac{3}{5}\) =
Answer: 9/25
Question 22.
\(\frac{3}{5}\) × \(\frac{4}{5}\) =
Answer: 12/25
Question 23.
\(\frac{3}{5}\) × \(\frac{5}{4}\) =
Answer: 15/20
Question 24.
\(\frac{4}{5}\) × \(\frac{5}{3}\) =
Answer: 20/15
Question 25.
\(\frac{1}{4}\) × \(\frac{1}{4}\) =
Answer: 1/16
Question 26.
\(\frac{1}{4}\) × \(\frac{3}{4}\) =
Answer: 3/16
Question 27.
\(\frac{3}{4}\) × \(\frac{3}{4}\) =
Answer: 9/16
Question 28.
\(\frac{3}{4}\) × \(\frac{4}{3}\) =
Answer: 12/12
Question 29.
\(\frac{3}{4}\) × \(\frac{5}{4}\) =
Answer: 15/16
Question 30.
\(\frac{3}{4}\) × \(\frac{6}{4}\) =
Answer: 18/16
Question 31.
\(\frac{4}{3}\) × \(\frac{4}{6}\) =
Answer: 16/18
Question 32.
\(\frac{2}{3}\) × \(\frac{1}{5}\) =
Answer: 2/15
Question 33.
\(\frac{2}{3}\) × \(\frac{4}{5}\) =
Answer: 8/15
Question 34.
\(\frac{2}{3}\) × \(\frac{5}{5}\) =
Answer: 10/15
Question 35.
\(\frac{2}{3}\) × \(\frac{6}{5}\) =
Answer: 12/15
Question 36.
\(\frac{1}{3}\) × \(\frac{6}{5}\) =
Answer: 6/15
Question 37.
\(\frac{1}{9}\) × \(\frac{1}{9}\) =
Answer: 1/81
Question 38.
\(\frac{1}{5}\) × \(\frac{3}{8}\) =
Answer: 3/40
Question 39.
\(\frac{3}{4}\) × \(\frac{1}{6}\) =
Answer: 3/24
Question 40.
\(\frac{2}{3}\) × \(\frac{2}{3}\) =
Answer: 4/9
Question 41.
\(\frac{3}{4}\) × \(\frac{8}{8}\) =
Answer: 24/32
Question 42.
\(\frac{2}{3}\) × \(\frac{6}{3}\) =
Answer: 12/9
Question 43.
\(\frac{6}{7}\) × \(\frac{8}{9}\) =
Answer: 48/63
Question 44.
\(\frac{7}{12}\) × \(\frac{8}{7}\) =
Answer: 72/84
Eureka Math Grade 5 Module 5 Lesson 7 Problem Set Answer Key
Geoffrey builds rectangular planters.
Question 1.
Geoffrey’s first planter is 8 feet long and 2 feet wide. The container is filled with soil to a height of 3 feet in the planter. What is the volume of soil in the planter? Explain your work using a diagram.
Answer:

Volume = length x width x height ‘
V = 8 feet x 2 feet x 3 feet
V = 48 cubic feet
Therefore, the volume of the soil in the planter = 48 cubic feet
Question 2.
Geoffrey wants to grow some tomatoes in four large planters. He wants each planter to have a volume of 320 cubic feet, but he wants them all to be different. Show four different ways Geoffrey can make these planters, and draw diagrams with the planters’ measurements on them.
Planter A
Planter B
Planter C
Planter D
Answer:

Question 3.
Geoffrey wants to make one planter that extends from the ground to just below his back window. The window starts 3 feet off the ground. If he wants the planter to hold 36 cubic feet of soil, name one way he could build the planter so it is not taller than 3 feet. Explain how you know.
Answer:
Given that, the window starts 3 feet off the ground
36 cubic feet can be shown as 36/2 = 12
12/3 = 4
So, the measurements of the planter to hold 36 cubic feet of soil
= 4 feet by 3 feet by 3 feet.
Volume : 36 cubic units
Question 4.
After all of this gardening work, Geoffrey decides he needs a new shed to replace the old one. His current shed is a rectangular prism that measures 6 feet long by 5 feet wide by 8 feet high. He realizes he needs a shed with 480 cubic feet of storage.
a. Will he achieve his goal if he doubles each dimension? Why or why not?
b. If he wants to keep the height the same, what could the other dimensions be for him to get the volume he wants?
c. If he uses the dimensions in part (b), what could be the area of the new shed’s floor?
Answer:
a.
The volume of the current shed = length x width x height
V = 6 x 5 x 8
V = 240 cubic feet.
According to given condition, if he doubles each dimension.
Then the volume = 12 x 10 x 16
= 1920 cubic feet
Therefore, he did not achieve his goal
To make 480 cubic feet he only needs to double one dimension but not all the three dimensions.
b.
The other dimensions of the shed to calculate the same volume by keeping the height same =
Height = 8 feet and volume = 480 cubic feet.
Other dimension =
length = 12 feet and width = 5 feet
or
length = 6 feet and width = 8 feet
c.
Area = length x width
According to the dimensions part b
Area = 12 x 5
A = 60
Therefore, the area of the new shed’s floor = 60 square feet.
Eureka Math Grade 5 Module 5 Lesson 7 Exit Ticket Answer Key
A storage shed is a rectangular prism and has dimensions of 6 meters by 5 meters by 12 meters. If Jean were to double these dimensions, she believes she would only double the volume. Is she correct? Explain why or why not. Include a drawing in your explanation.
Answer:
Volume = length x width x height
V = 6 x 5 x 12
V = 360 cubic metres
According to given condition of doubling the volume, then
Volume = 2880 cubic metres.
288 cubic metres is much larger than 360 cubic metres. So, volume will not be double.


Eureka Math Grade 5 Module 5 Lesson 7 Homework Answer Key
Wren makes some rectangular display boxes.
Question 1.
Wren’s first display box is 6 inches long, 9 inches wide, and 4 inches high. What is the volume of the display box? Explain your work using a diagram.
Answer:

Volume = length x width x volume
V = 6 x 9 x 4
V = 216 cubic inches
Therefore, volume of the display box = 216 cubic inches
Question 2.
Wren wants to put some artwork into three shadow boxes. She knows they all need a volume of 60 cubic inches, but she wants them all to be different. Show three different ways Wren can make these boxes by drawing diagrams and labeling the measurements.
Shadow Box A
Shadow Box B
Shadow Box C
Answer:

Question 3.
Wren wants to build a box to organize her scrapbook supplies. She has a stencil set that is 12 inches wide that needs to lay flat in the bottom of the box. The supply box must also be no taller than 2 inches. Name one way she could build a supply box with a volume of 72 cubic inches.
Answer:
Give, the height of the supply box should not be taller than 2 inches
72 cubic inches can be shown as
72/2 = 36
Now, 36/2 = 18
So, the measurements of the box are 18 inches by 2 inches by 2 inches
Therefore, Wren can use a box of 18 by 2 by 2 by inches box
Question 4.
After all of this organizing, Wren decides she also needs more storage for her soccer equipment. Her current storage box measures 1 foot long by 2 feet wide by 2 feet high. She realizes she needs to replace it with a box with 12 cubic feet of storage, so she doubles the width.
a. Will she achieve her goal if she does this? Why or why not?
b. If she wants to keep the height the same, what could the other dimensions be for a 12-cubic-foot storage box?
c. If she uses the dimensions in part (b), what is the area of the new storage box’s floor?
d. How has the area of the bottom in her new storage box changed? Explain how you know.
Answer:
a.
Given, the measurements of the storage box = 1 foot long by 2 feet wide by 2 feet high.
Volume = length x width x height
V = 1 x 2 x 2
V = 4 cubic feet
By doubling the width, volume = 1 x 4 x 2
V = 8 cubic feet
Therefore, she did not achieve her goal by doubling the width.
b.

The other dimensions to be for a 12 cubic feet by keeping the height same =
3 x 2 x 2
Volume = 3 x 2 x 2 = 12
c.
The area of the storage box =
3 inches x 2 inches
A = 6 square feet
d.
The area of first storage box = 4 square feet and
The area of first storage box = 6 square feet.