Engage NY Eureka Math 7th Grade Module 1 Lesson 12 Answer Key
Eureka Math Grade 7 Module 1 Lesson 12 Example Answer Key
Example 1.
Time to Remodel
You have decided to remodel your bathroom and install a tile floor. The bathroom is in the shape of a rectangle, and the floor measures 14 feet, 8 inches long by 5 feet, 6 inches wide. The tiles you want to use cost $5 each, and each tile covers 4\(\frac{2}{3}\) square feet. If you have $100 to spend, do you have enough money to complete the project?
Make a Plan: Complete the chart to identify the necessary steps in the plan and find a solution.
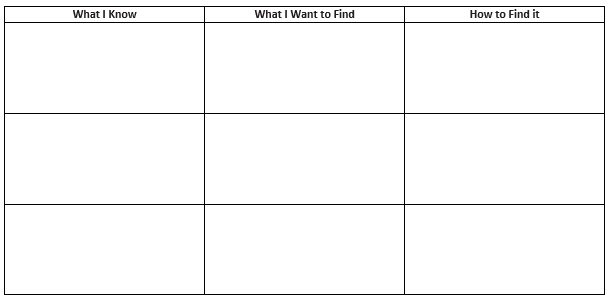
Answer:
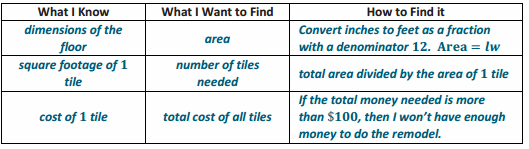
Compare your plan with a partner. Using your plans, work together to determine how much money you will need to complete the project and if you have enough money.
Answer:
Dimensions:
5 ft.,6 in.=5 \(\frac{1}{2}\) ft.
14 ft.,8 in.= 14 \(\frac{2}{3}\) ft.
Area (square feet):
A = lw
A = (5 \(\frac{1}{2}\) ft.)(14 \(\frac{2}{3}\) ft.)
A = (\(\frac{11}{2}\) ft.)(\(\frac{44}{3}\) ft.)
A = \(\frac{242}{3}\) = 80 \(\frac{2}{3}\)2
Number of Tiles:
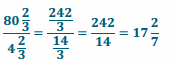
I cannot buy part of a tile, so I will need to purchase 18 tiles.
Total Cost: 18(5)=$90
Do I have enough money?
Yes. Since the total is less than $100, I have enough money.
Generate discussion about completing the plan and finding the solution. If needed, pose the following questions:
→ Why was the mathematical concept of area, and not perimeter or volume, used?
→ Area was used because we were “covering” the rectangular floor. Area is 2 dimensional, and we were given two dimensions, length and width of the room, to calculate the area of the floor. If we were just looking to put trim around the outside, then we would use perimeter. If we were looking to fill the room from floor to ceiling, then we would use volume.
→ Why would 5.6 inches and 14.8 inches be incorrect representations for 5 feet, 6 inches and 14 feet, 8 inches?
→ The relationship between feet and inches is 12 inches for every 1 foot. To convert to feet, you need to figure out what fractional part 6 inches is of a foot, or 12 inches. If you just wrote 5.6, then you would be basing the inches out of 10 inches, not 12 inches. The same holds true for 14 feet, 8 inches.
→ How is the unit rate useful?
→ The unit rate for a tile is given as 4 \(\frac{2}{3}\) . We can find the total number of tiles needed by dividing the area (total square footage) by the unit rate.
→ Can I buy 17 \(\frac{2}{7}\) tiles?
→ No, you have to buy whole tiles and cut what you may need.
→ How would rounding to 17 tiles instead of rounding to 18 tiles affect the job?
→ Even though the rules of rounding would say round down to 17 tiles, we would not in this problem. If we round down, then the entire floor would not be covered, and we would be short. If we round up to 18 tiles, the entire floor would be covered with a little extra.
Eureka Math Grade 7 Module 1 Lesson 12 Exercise Answer Key
Which car can travel farther on 1 gallon of gas?
Blue Car: travels 18 \(\frac{2}{5}\) miles using 0.8 gallons of gas
Red Car: travels 17 \(\frac{2}{5}\) miles using 0.75 gallons of gas
Answer:
Finding the Unit Rate:

Rate:
![]()
The red car traveled \(\frac{1}{5}\) mile farther on one gallon of gas.
Eureka Math Grade 7 Module 1 Lesson 12 Problem Set Answer Key
Question 1.
You are getting ready for a family vacation. You decide to download as many movies as possible before leaving for the road trip. If each movie takes 1 \(\frac{2}{5}\) hours to download, and you downloaded for 5 \(\frac{1}{4}\) hours, how many movies did you download?
Answer:
3 \(\frac{3}{4}\) movies; however, since you cannot download \(\frac{3}{4}\) of a movie, then you downloaded 3 movies.
Question 2.
The area of a blackboard is 1\(\frac{1}{3}\) square yards. A poster’s area is \(\frac{8}{9}\) square yards. Find the unit rate and explain, in words, what the unit rate means in the context of this problem. Is there more than one unit rate that can be calculated? How do you know?
Answer:
1 \(\frac{1}{2}\) . The area of the blackboard is 1 \(\frac{1}{2}\) times the area of the poster.
Yes. There is another possible unit rate: \(\frac{2}{3}\). The area of the poster is \(\frac{2}{3}\) the area of the blackboard.
Question 3.
A toy jeep is 12 \(\frac{1}{2}\) inches long, while an actual jeep measures 18 \(\frac{3}{4}\) feet long. What is the value of the ratio of the length of the toy jeep to the length of the actual jeep? What does the ratio mean in this situation?
Answer:
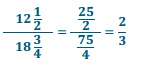
Every 2 inches in length on the toy jeep corresponds to 3 feet in length on the actual jeep.
Question 4.
To make 5 dinner rolls, \(\frac{1}{3}\) cup of flour is used.
a. How much flour is needed to make one dinner roll?
Answer:
\(\frac{1}{15}\) cup
b. How many cups of flour are needed to make 3 dozen dinner rolls?
Answer:
2 \(\frac{2}{5}\) cups
c. How many rolls can you make with 5 \(\frac{2}{3}\) cups of flour?
Answer:
85 rolls
Eureka Math Grade 7 Module 1 Lesson 12 Exit Ticket Answer Key
If 3\(\frac{3}{4}\) lb. of candy cost $20.25, how much would 1 lb. of candy cost?
Answer:
5 \(\frac{2}{5}\) = 5.4
One pound of candy would cost $5.40.
Students may find the unit rate by first converting $20.25 to \(\frac{81}{4}\) and then dividing by \(\frac{15}{4}\).