Engage NY Eureka Math 8th Grade Module 5 Lesson 6 Answer Key
Eureka Math Grade 8 Module 5 Lesson 6 Exercise Answer Key
Exercise
A function assigns to the inputs shown the corresponding outputs given in the table below.
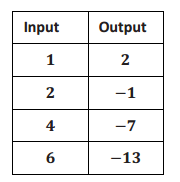
a. Do you suspect the function is linear? Compute the rate of change of this data for at least three pairs of inputs and their corresponding outputs.
Answer:
\(\frac{2 – ( – 1)}{1 – 2}\) = \(\frac{3}{ – 1}\)
= – 3
\(\frac{ – 7 – ( – 13)}{4 – 6}\) = \(\frac{6}{ – 2}\)
= – 3
\(\frac{2 – ( – 7)}{1 – 4}\) = \(\frac{9}{ – 3}\)
= – 3
Yes, the rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to – 3. Since the rate of change is the same, then I know it is a linear function.
b. What equation seems to describe the function?
Answer:
Using the assignment of 2 to 1:
2 = – 3(1) + b
2 = – 3 + b
5 = b
The equation that seems to describe the function is y = – 3x + 5.
c. As you did not verify that the rate of change is constant across all input/output pairs, check that the equation you found in part (a) does indeed produce the correct output for each of the four inputs 1, 2, 4, and 6.
Answer:
For x = 1 we have y = – 3(1) + 5 = 2.
For x = 2 we have y = – 3(2) + 5 = – 1.
For x = 4 we have y = – 3(4) + 5 = – 7.
For x = 6 we have y = – 3(6) + 5 = – 13.
These are correct.
d. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be a plot of four points lying on a common line. As we were not told about any other inputs for this function, we must assume for now that there are only these four input values for the function.
The four points lie on the line with equation y = – 3x + 5.
Eureka Math Grade 8 Module 5 Lesson 6 Problem Set Answer Key
Question 1.
A function assigns to the inputs given the corresponding outputs shown in the table below.
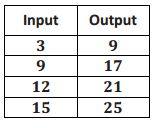
a. Does the function appear to be linear? Check at least three pairs of inputs and their corresponding outputs.
\(\frac{9 – 17}{3 – 9}\) = \(\frac{ – 8}{ – 6}\)
= \(\frac{4}{3}\)
\(\frac{17 – 21}{9 – 12}\) = \(\frac{ – 4}{ – 3}\)
= \(\frac{4}{3}\)
\(\frac{21 – 25}{12 – 15}\) = \(\frac{ – 4}{ – 3}\)
= \(\frac{4}{3}\)
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to \(\frac{4}{3}\). Since the rate of change is the same, the function does appear to be linear.
b. Find a linear equation that describes the function.
Answer:
Using the assignment of 9 to 3
9 = \(\frac{4}{3}\) (3) + b
9 = 4 + b
5 = b
The equation that describes the function is y = \(\frac{4}{3}\) x + 5. (We check that for each of the four inputs given, this equation does indeed produce the correct matching output.)
c. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be four points in a row. They all lie on the line given by the equation
y = \(\frac{4}{3}\) x + 5.
Question 2.
A function assigns to the inputs given the corresponding outputs shown in the table below.
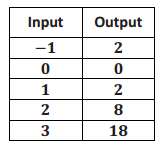
a. Is the function a linear function?
Answer:
\(\frac{2 – 0}{ – 1 – 0}\) = \(\frac{2}{ – 1}\)
= – 2
\(\frac{0 – 2}{0 – 1}\) = \(\frac{ – 2}{ – 1}\)
= 2
No. The rate of change is not the same when I check the first two pairs of inputs and corresponding outputs. All rates of change must be the same for all inputs and outputs for the function to be linear.
b. What equation describes the function?
Answer:
I am not sure what equation describes the function. It is not a linear function.
Question 3.
A function assigns the inputs and corresponding outputs shown in the table below.
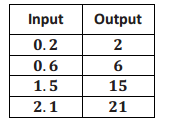
a. Does the function appear to be linear? Check at least three pairs of inputs and their corresponding outputs..
Answer:
\(\frac{2 – 6}{0.2 – 0.6}\) = \(\frac{ – 4}{ – 0.4}\)
= 10
\(\frac{6 – 15}{0.6 – 1.5}\) = \(\frac{ – 9}{ – 0.9}\)
= 10
\(\frac{15 – 21}{1.5 – 2.1}\) = \(\frac{ – 6}{ – 0.6}\)
= 10
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to 10. The function appears to be linear.
b. Find a linear equation that describes the function.
Answer:
Using the assignment of 2 to 0.2:
2 = 10(0.2) + b
2 = 2 + b
0 = b
The equation that describes the function is y = 10x . It clearly fits the data presented in the table.
c. What will the graph of the function look like? Explain.
Answer:
The graph will be four distinct points in a row. They all sit on the line given by the equation y = 10x.
Question 4.
Martin says that you only need to check the first and last input and output values to determine if the function is linear. Is he correct? Explain.
Answer:
No, he is not correct. For example, consider the function with input and output values in this table.
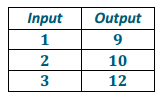
Using the first and last input and output, the rate of change is
\(\frac{9 – 12}{1 – 3}\) = \(\frac{ – 3}{ – 2}\)
= \(\frac{3}{2}\)
But when you use the first two inputs and outputs, the rate of change is
\(\frac{9 – 10}{1 – 2}\) = \(\frac{ – 1}{ – 1}\)
= 1
Note to teacher: Accept any example where the rate of change is different for any two inputs and outputs.
Question 5.
Is the following graph a graph of a linear function? How would you determine if it is a linear function?
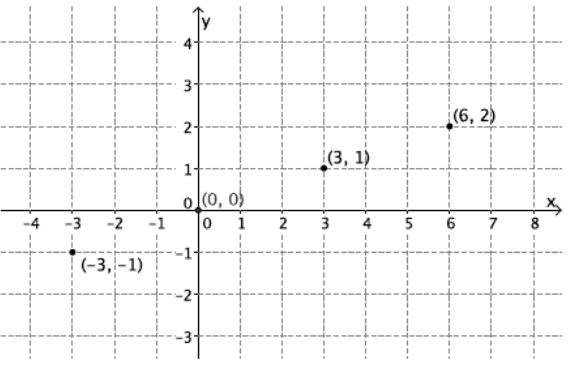
Answer:
It appears to be a linear function. To check, I would organize the coordinates in an input and output table. Next, I would check to see that all the rates of change are the same. If they are the same rates of change, I would use the equation y = mx + b and one of the assignments to write an equation to solve for b. That information would allow me to determine the equation that represents the function.
Question 6.
A function assigns to the inputs given the corresponding outputs shown in the table below.
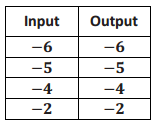
a. Does the function appear to be a linear function?
Answer:
\(\frac{ – 6 – ( – 5)}{ – 6 – ( – 5)}\) = \(\frac{1}{1}\)
= 1
\(\frac{ – 5 – ( – 5)}{ – 5 – ( – 5)}\) = \(\frac{1}{1}\)
= 1
\(\frac{ – 4 – ( – 2)}{ – 4 – ( – 2)}\) = \(\frac{2}{2}\)
= 1
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to 1. Since the rate of change is constant so far, it could be a linear function.
b. What equation describes the function?
Answer:
Clearly the equation y = x fits the data. It is a linear function.
c. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be four distinct points in a row. These four points lie on the line given by the equation y = x.
Eureka Math Grade 8 Module 5 Lesson 6 Exit Ticket Answer Key
Question 1.
Sylvie claims that a function with the table of inputs and outputs below is a linear function. Is she correct? Explain.
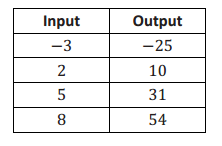
Answer:
\(\frac{ – 25 – (10)}{ – 3 – 2}\) = \(\frac{ – 35}{ – 5}\)
= 7
\(\frac{10 – 31}{2 – 5}\) = \(\frac{ – 21}{ – 3}\)
= 7
\(\frac{31 – 54}{5 – 8}\) = \(\frac{ – 23}{ – 3}\)
= \(\frac{23}{3}\)
No, this is not a linear function. The rate of change was not the same for each pair of inputs and outputs inspected, which means that it is not a linear function.
Question 2.
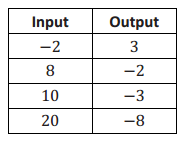
A function assigns the inputs and corresponding outputs shown in the table to the right.
a. Does the function appear to be linear? Check at least three pairs of inputs and their corresponding outputs.
Answer:
\(\frac{3 – ( – 2)}{ – 2 – 8}\) = \(\frac{5}{ – 10}\) = – \(\frac{1}{2}\)
\(\frac{ – 2 – ( – 3)}{8 – 10}\) = \(\frac{1}{ – 2}\) = – \(\frac{1}{2}\)
\(\frac{ – 3 – ( – 8)}{10 – 20}\) = \(\frac{5}{ – 10}\) = – \(\frac{1}{2}\)
Yes. The rate of change is the same when I check pairs of inputs and corresponding outputs. Each time it is equal to – \(\frac{1}{2}\) . Since the rate of change is the same for at least these three examples, the function could well be linear.
b. Can you write a linear equation that describes the function?
Answer:
We suspect we have an equation of the form y = – \(\frac{1}{2}\) x + b. Using the assignment of 3 to – 2:
3 = – \(\frac{1}{2}\) ( – 2) + b
3 = 1 + b
2 = b
The equation that describes the function might be y = – \(\frac{1}{2}\) x + 2.
Checking: When x = – 2, we get y = – \(\frac{1}{2}\) ( – 2) + 2 = 3. When x = 8, we get y = – \(\frac{1}{2}\) (8) + 2 = – 2. When x = 10, we get y = – \(\frac{1}{2}\) (10) + 2 = – 3. When x = 20, we get y = – \(\frac{1}{2}\) (20) + 2 = – 8.
It works.
c. What will the graph of the function look like? Explain.
Answer:
The graph of the function will be four distinct points all lying in a line. (They all lie on the line with equation y = – \(\frac{1}{2}\) x + 2 ).
Eureka Math Grade 8 Module 5 Lesson 6 Multi – Step Equations I Answer Key
Set 1:
3x + 2 = 5x + 6
4(5x + 6) = 4(3x + 2)
\(\frac{3x + 2}{6}\) = \(\frac{5x + 6}{6}\)
Answer:
Answer for each problem in this set is x = – 2.
Set 2:
6 – 4x = 10x + 9
– 2( – 4x + 6) = – 2(10x + 9)
\(\frac{10x + 9}{5}\) = \(\frac{6 – 4x}{5}\)
Answer:
Answer for each problem in this set is x = – \(\frac{3}{14}\).
Set 3:
5x + 2 = 9x – 18
8x + 2 – 3x = 7x – 18 + 2x
\(\frac{2 + 5x}{3}\) = \(\frac{7x – 18 + 2x}{3}\)
Answer:
Answer for each problem in this set is x = 5.