Engage NY Eureka Math 8th Grade Module 5 Lesson 11 Answer Key
Eureka Math Grade 8 Module 5 Lesson 11 Example Answer Key
Example 1.
Compute the exact volume for the sphere shown below.
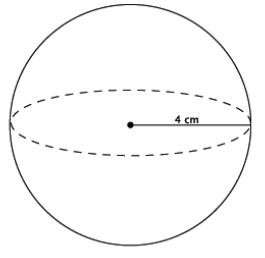
Answer:
Provide students time to work; then, have them share their solutions.
Sample student work:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(43 )
= \(\frac{4}{3}\) π(64)
= \(\frac{256}{3}\) π
= 85 \(\frac{1}{3}\) π
The volume of the sphere is 85 \(\frac{1}{3}\) π cm3.
Example 2.
A cylinder has a diameter of 16 inches and a height of 14 inches. What is the volume of the largest sphere that will fit into the cylinder?
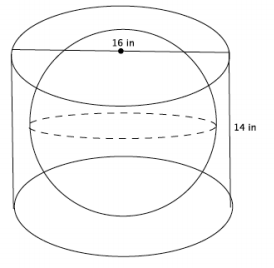
Answer:
→ What is the radius of the base of the cylinder?
The radius of the base of the cylinder is 8 inches.
→ Could the sphere have a radius of 8 inches? Explain.
No. If the sphere had a radius of 8 inches, then it would not fit into the cylinder because the height is only 14 inches. With a radius of 8 inches, the sphere would have a height of 2r, or 16 inches. Since the cylinder is only 14 inches high, the radius of the sphere cannot be 8 inches.
→ What size radius for the sphere would fit into the cylinder? Explain.
A radius of 7 inches would fit into the cylinder because 2r is 14, which means the sphere would touch the top and bottom of the cylinder. A radius of 7 means the radius of the sphere would not touch the sides of the cylinder, but would fit into it.
→ Now that we know the radius of the largest sphere is 7 inches, what is the volume of the sphere?
Sample student work:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(73 )
= \(\frac{4}{3}\) π(343)
= \(\frac{1372}{3}\) π
= 457 \(\frac{1}{3}\) π
The volume of the sphere is 457 \(\frac{1}{3}\) π cm3.
Eureka Math Grade 8 Module 5 Lesson 11 Exercise Answer Key
Exercises 1–3
Exercise 1.
What is the volume of a cylinder?
Answer:
V = πr2 h
Exercise 2.
What is the height of the cylinder?
Answer:
The height of the cylinder is the same as the diameter of the sphere. The diameter is 2r.
Exercise 3.
If volume(sphere) = 2/3 volume(cylinder with same diameter and height), what is the formula for the volume of a sphere?
Answer:
Volume(sphere) = \(\frac{2}{3}\) (πr2h)
Volume(sphere) = \(\frac{2}{3}\) (πr22r)
Volume(sphere) = \(\frac{4}{3}\) (πr3)
Exercises 4–8
Exercise 4.
Use the diagram and the general formula to find the volume of the sphere.
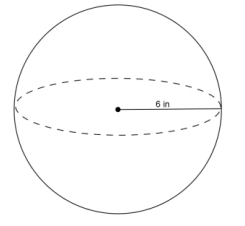
Answer:
V = \(\frac{4}{3}\) πr3
V = \(\frac{4}{3}\) π(63 )
V ≈ 288π
The volume of the sphere is about 288π in3.
Exercise 5.
The average basketball has a diameter of 9.5 inches. What is the volume of an average basketball? Round your answer to the tenths place.
Answer:
V = \(\frac{4}{3}\) πr3
V = \(\frac{4}{3}\) π(4.753 )
V = \(\frac{4}{3}\) π(107.17)
V ≈ 142.9π
The volume of an average basketball is about 142.9π in3.
Exercise 6.
A spherical fish tank has a radius of 8 inches. Assuming the entire tank could be filled with water, what would the volume of the tank be? Round your answer to the tenths place.
Answer:
V = \(\frac{4}{3}\) πr3
V = \(\frac{4}{3}\) π(83 )
V = \(\frac{4}{3}\) π(512)
V ≈ 682.7π
The volume of the fish tank is about 682.7π in3.
Exercise 7.
Use the diagram to answer the questions.
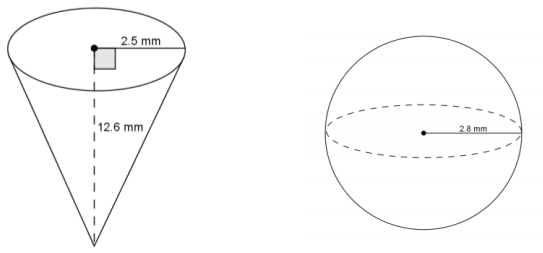
a. Predict which of the figures shown above has the greater volume. Explain.
Answer:
Student answers will vary. Students will probably say the cone has more volume because it looks larger.
b. Use the diagram to find the volume of each, and determine which has the greater volume.
Answer:
V = \(\frac{1}{3}\) πr2 h
V = \(\frac{1}{3}\) π(2.52)(12.6)
V = 26.25π
The volume of the cone is 26.25π mm3.
V = \(\frac{4}{3}\) πr3
V = \(\frac{4}{3}\) π(2.83)
V = 29.269333…π
The volume of the sphere is about 29.27π mm3. The volume of the sphere is greater than the volume of the cone.
Exercise 8.
One of two half spheres formed by a plane through the sphere’s center is called a hemisphere. What is the formula for the volume of a hemisphere?
Answer:
Since a hemisphere is half a sphere, the volume(hemisphere) = \(\frac{1}{2}\) (volume of sphere).
V = \(\frac{1}{2}\) (\(\frac{4}{3}\) πr3 )
V = \(\frac{2}{3}\) πr3
Eureka Math Grade 8 Module 5 Lesson 11 Problem Set Answer Key
Question 1.
Use the diagram to find the volume of the sphere.
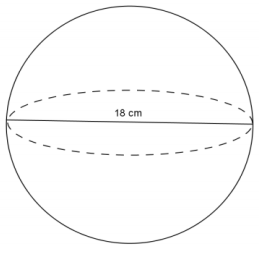
Answer:
V = \(\frac{4}{3}\) πr3
V = \(\frac{4}{3}\) π(93)
V = 972π
The volume of the sphere is 972π cm3.
Question 2.
Determine the volume of a sphere with diameter 9 mm, shown below.
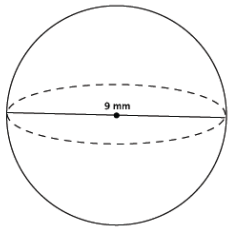
Answer:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(4.53 )
= \(\frac{364.5}{3}\) π
= 121.5π
The volume of the sphere is 121.5π mm3.
Question 3.
Determine the volume of a sphere with diameter 22 in., shown below.
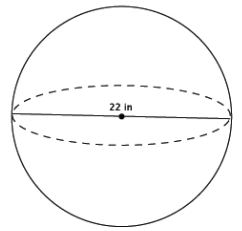
Answer:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(113 )
= \(\frac{5324}{3}\) π
= 1774 \(\frac{2}{3}\) π
The volume of the sphere is 1774 \(\frac{2}{3}\) π in3.
Question 4.
Which of the two figures below has the lesser volume?
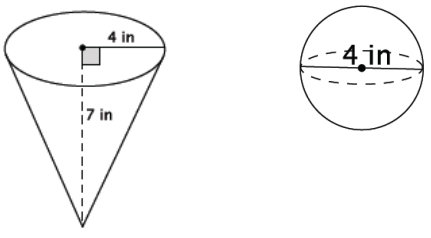
Answer:
The volume of the cone:
V = \(\frac{1}{3}\) πr2 h
= \(\frac{1}{3}\) π(16)(7)
= \(\frac{112}{3}\) π
= 37 \(\frac{1}{3}\) π
The volume of the sphere:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(23 )
= \(\frac{32}{3}\) π
= 10 \(\frac{2}{3}\) π
The cone has volume 37 \(\frac{1}{3}\) π in3 and the sphere has volume 10 \(\frac{2}{3}\) π in3. The sphere has the lesser volume.
Question 5.
Which of the two figures below has the greater volume?
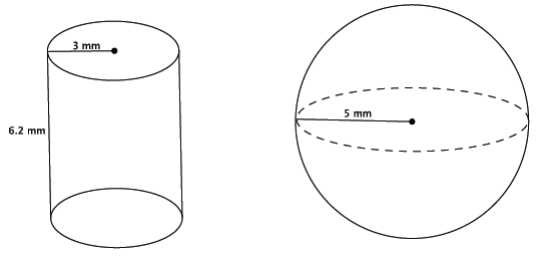
Answer:
The volume of the cylinder:
V = πr2 h
= π(32)(6.2)
= 55.8π
The volume of the sphere:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(53)
= \(\frac{500}{3}\) π
= 166 \(\frac{2}{3}\) π
The cylinder has volume 55.8π mm3 and the sphere has volume 166 \(\frac{2}{3}\) π mm3. The sphere has the greater volume.
Question 6.
Bridget wants to determine which ice cream option is the best choice. The chart below gives the description and prices for her options. Use the space below each item to record your findings.
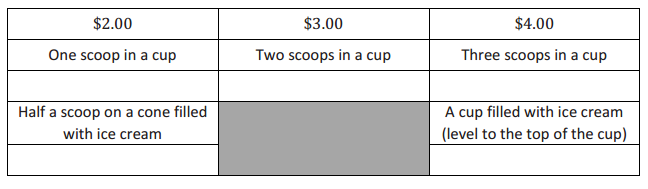
A scoop of ice cream is considered a perfect sphere and has a 2-inch diameter. A cone has a 2-inch diameter and a height of 4.5 inches. A cup, considered a right circular cylinder, has a 3-inch diameter and a height of 2 inches.
Answer:

a. Determine the volume of each choice. Use 3.14 to approximate π.
Answer:
First, find the volume of one scoop of ice cream.
Volume of one scoop = \(\frac{4}{3}\) π(13)
The volume of one scoop of ice cream is \(\frac{4}{3}\) π in3, or approximately 4.19 in3.
The volume of two scoops of ice cream is \(\frac{8}{3}\) π in3, or approximately 8.37 in3.
The volume of three scoops of ice cream is \(\frac{12}{3}\) π in3, or approximately 12.56 in3.
Volume of half scoop = \(\frac{2}{3}\) π(13)
The volume of half a scoop of ice cream is \(\frac{2}{3}\) π in3, or approximately 2.09 in3.
Volume of cone = \(\frac{1}{3}\) (πr2)h
V = \(\frac{1}{3}\) π(12)4.5
V = 1.5π
The volume of the cone is 1.5π in3, or approximately 4.71 in3. Then, the cone with half a scoop of ice cream on top is approximately 6.8 in3.
V = πr2 h
V = π1.52(2)
V = 4.5π
The volume of the cup is 4.5π in3, or approximately 14.13 in3.
b. Determine which choice is the best value for her money. Explain your reasoning.
Answer:
Student answers may vary.
Checking the cost for every in3 of each choice:
\(\frac{2}{4.19}\) ≈ 0.47723…
\(\frac{2}{6.8}\) ≈ 0.29411…
\(\frac{3}{8.37}\) ≈ 0.35842…
\(\frac{4}{12.56}\) ≈ 0.31847…
\(\frac{4}{14.13}\) ≈ 0.28308…
The best value for her money is the cup filled with ice cream since it costs about 28 cents for every in3.
Eureka Math Grade 8 Module 5 Lesson 11 Exit Ticket Answer Key
Question 1.
What is the volume of the sphere shown below?
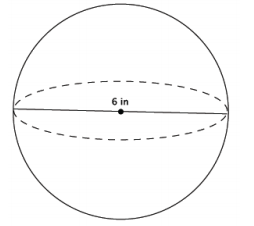
Answer:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(33 )
= \(\frac{108}{3}\) π
= 36π
The volume of the sphere is 36π in3.
Question 2.
Which of the two figures below has the greater volume?
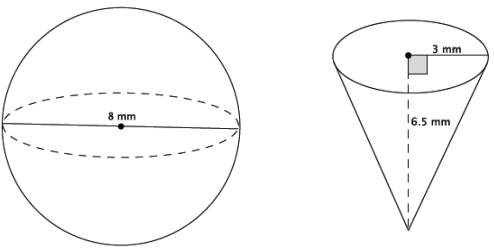
Answer:
V = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) π(43)
= \(\frac{256}{3}\) π
= 85 \(\frac{1}{3}\) π
The volume of the sphere is 85 \(\frac{1}{3}\) π mm3.
V = \(\frac{1}{3}\) πr2 h
= \(\frac{1}{3}\) π(32)(6.5)
= \(\frac{58.5}{3}\) π
= 19.5π
The volume of the cone is 19.5π mm3. The sphere has the greater volume.