Engage NY Eureka Math 8th Grade Module 5 Lesson 7 Answer Key
Eureka Math Grade 8 Module 5 Lesson 7 Exploratory Challenge/Exercise Answer Key
Exploratory Challenge/Exercises 1–4
Each of Exercises 1–4 provides information about two functions. Use that information given to help you compare the two functions and answer the questions about them.
Exercise 1.
Alan and Margot each drive from City A to City B, a distance of 147 miles. They take the same route and drive at constant speeds. Alan begins driving at 1:40 p.m. and arrives at City B at 4:15 p.m. Margot’s trip from City A to City B can be described with the equation y = 64x, where y is the distance traveled in miles and x is the time in minutes spent traveling. Who gets from City A to City B faster?
Answer:
Student solutions will vary. Sample solution is provided.
It takes Alan 155 minutes to travel the 147 miles. Therefore, his constant rate is \(\frac{147}{155}\) miles per minute.
Margot drives 64 miles per hour (60 minutes). Therefore, her constant rate is \(\frac{64}{60}\) miles per minute.
To determine who gets from City A to City B faster, we just need to compare their rates in miles per minute.
\(\frac{147}{155}\) < \(\frac{64}{60}\)
Since Margot’s rate is faster, she will get to City B faster than Alan.
Exercise 2.
You have recently begun researching phone billing plans. Phone Company A charges a flat rate of $75 a month. A flat rate means that your bill will be $75 each month with no additional costs. The billing plan for Phone Company B is a linear function of the number of texts that you send that month. That is, the total cost of the bill changes each month depending on how many texts you send. The table below represents some inputs and the corresponding outputs that the function assigns.
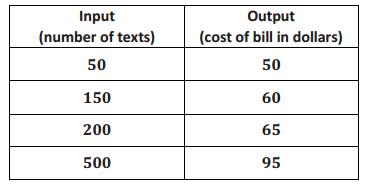
At what number of texts would the bill from each phone plan be the same? At what number of texts is Phone Company A the better choice? At what number of texts is Phone Company B the better choice?
Answer:
Student solutions will vary. Sample solution is provided.
The equation that represents the function for Phone Company A is y = 75.
To determine the equation that represents the function for Phone Company B, we need the rate of change. (We are told it is constant.)
\(\frac{60 – 50}{150 – 50}\) = \(\frac{10}{100}\)
= 0.1
The equation for Phone Company B is shown below.
Using the assignment of 50 to 50,
50 = 0.1(50) + b
50 = 5 + b
45 = b.
The equation that represents the function for Phone Company B is y = 0.1x + 45.
We can determine at what point the phone companies charge the same amount by solving the system:
y = 75
y = 0.1x + 45
75 = 0.1x + 45
30 = 0.1x
300 = x
After 300 texts are sent, both companies would charge the same amount, $75. More than 300 texts means that the bill from Phone Company B will be higher than Phone Company A. Less than 300 texts means the bill from Phone Company A will be higher.
Exercise 3.
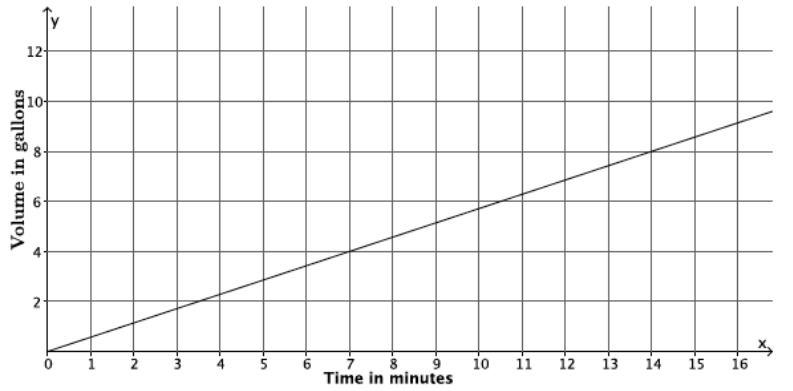
The function that gives the volume of water, y, that flows from Faucet A in gallons during x minutes is a linear function with the graph shown. Faucet B’s water flow can be described by the equation y = \(\frac{5}{6}\) x, where y is the volume of water in gallons that flows from the faucet during x minutes. Assume the flow of water from each faucet is constant. Which faucet has a faster rate of flow of water? Each faucet is being used to fill a tub with a volume of 50 gallons. How long will it take each faucet to fill its tub? How do you know?
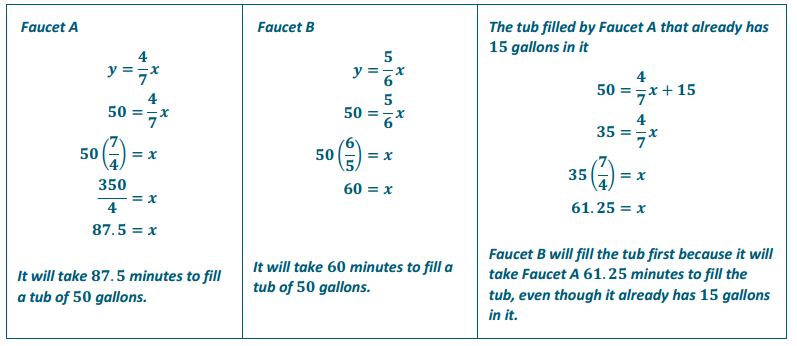
Suppose the tub being filled by Faucet A already had 15 gallons of water in it, and the tub being filled by Faucet B started empty. If now both faucets are turned on at the same time, which faucet will fill its tub fastest?
Answer:
Student solutions will vary. Sample solution is provided.
The slope of the graph of the line is \(\frac{4}{7}\) because (7, 4) is a point on the line that represents 4 gallons of water that flows in 7 minutes. Therefore, the rate of water flow for Faucet A is \(\frac{4}{7}\). To determine which faucet has a faster flow of water, we can compare their rates.
\(\frac{4}{7}\) < \(\frac{5}{6}\)
Therefore, Faucet B has a faster rate of water flow.
Exercise 4.
Two people, Adam and Bianca, are competing to see who can save the most money in one month. Use the table and the graph below to determine who will save the most money at the end of the month. State how much money each person had at the start of the competition. (Assume each is following a linear function in his or her saving habit.)
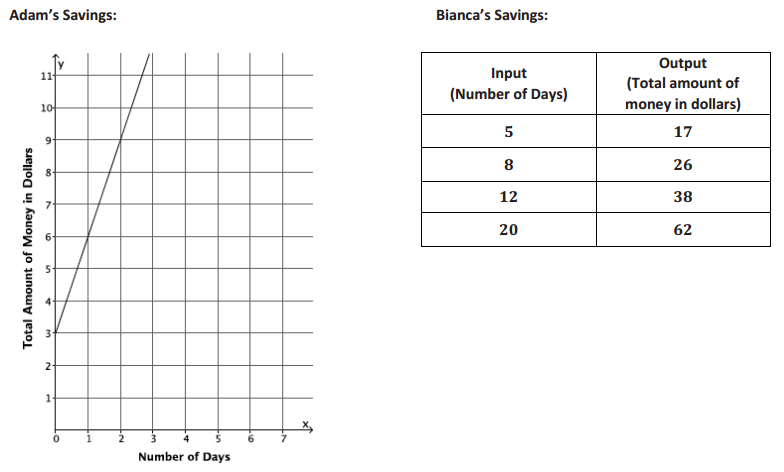
Answer:
The slope of the line that represents Adam’s savings is 3; therefore, the rate at which Adam is saving money is $3 per day. According to the table of values for Bianca, she is also saving money at a rate of $3 per day:
\(\frac{26 – 17}{8 – 5}\) = \(\frac{9}{3}\) = 3
\(\frac{38 – 26}{12 – 8}\) = \(\frac{12}{4}\) = 3
\(\frac{62 – 26}{20 – 8}\) = \(\frac{36}{12}\) = 3
Therefore, at the end of the month, Adam and Bianca will both have saved the same amount of money.
According to the graph for Adam, the equation y = 3x + 3 represents the function of money saved each day. On day zero, he had $3.
The equation that represents the function of money saved each day for Bianca is y = 3x + 2 because, using the assignment of 17 to 5
17 = 3(5) + b
17 = 15 + b
2 = b.
The amount of money Bianca had on day zero was $2.
Eureka Math Grade 8 Module 5 Lesson 7 Problem Set Answer Key
Question 1.
The graph below represents the distance in miles, y, Car A travels in x minutes. The table represents the distance in miles, y, Car B travels in x minutes. It is moving at a constant rate. Which car is traveling at a greater speed? How do you know?
Car A:
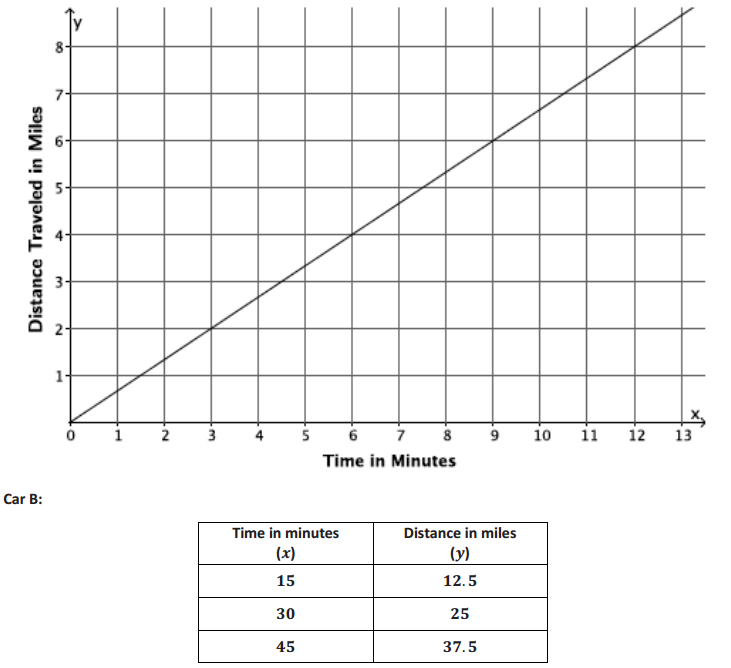
Answer:
Based on the graph, Car A is traveling at a rate of 2 miles every 3 minutes, m = 2/3. From the table, the constant rate that Car B is traveling is
\(\frac{25 – 12.5}{30 – 15}\) = \(\frac{12.5}{15}\) = \(\frac{25}{30}\) = \(\frac{5}{6}\).
Since \(\frac{5}{6}\)>\(\frac{2}{3}\), Car B is traveling at a greater speed.
Question 2.
The local park needs to replace an existing fence that is 6 feet high. Fence Company A charges $7,000 for building materials and $200 per foot for the length of the fence. Fence Company B charges are based solely on the length of the fence. That is, the total cost of the 6 – foot high fence will depend on how long the fence is. The table below represents some inputs and their corresponding outputs that the cost function for Fence Company B assigns. It is a linear function.
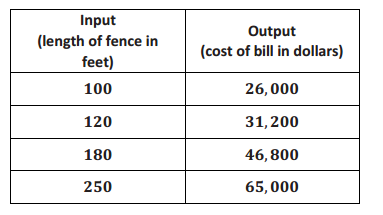
a. Which company charges a higher rate per foot of fencing? How do you know?
Answer:
Let x represent the length of the fence and y represent the total cost.
The equation that represents the function for Fence Company A is y = 200x + 7,000. So, the rate is 200 dollars per foot of fence.
The rate of change for Fence Company B is given by:
\(\frac{26,000 – 31,200}{100 – 120}\) = \(\frac{ – 5,200}{ – 20}\)
= 260
Fence Company B charges $260 per foot of fence, which is a higher rate per foot of fence length than Fence Company A.
b. At what number of the length of the fence would the cost from each fence company be the same? What will the cost be when the companies charge the same amount? If the fence you need were 190 feet in length, which company would be a better choice?
Answer:
Student solutions will vary. Sample solution is provided.
The equation for Fence Company B is
y = 260x.
We can find out at what point the fence companies charge the same amount by solving the system
y = 200x + 7000
y = 260x
200x + 7,000 = 260x
7,000 = 60x
116.6666…… = x
116.7 ≈ x
At 116.7 feet of fencing, both companies would charge the same amount (about $30,340). Less than 116.7 feet of fencing means that the cost from Fence Company A will be more than Fence Company B. More than 116.7 feet of fencing means that the cost from Fence Company B will be more than Fence Company A. So, for 190 feet of fencing, Fence Company A is the better choice.
Question 3.
The equation y = 123x describes the function for the number of toys, y, produced at Toys Plus in x minutes of production time. Another company, #1 Toys, has a similar function, also linear, that assigns the values shown in the table below. Which company produces toys at a slower rate? Explain.
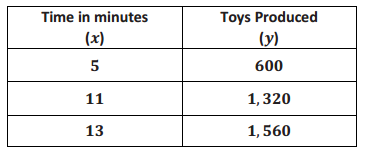
Answer:
We are told that #1 Toys produces toys at a constant rate. That rate is:
\(\frac{1,320 – 600}{11 – 5}\) = \(\frac{720}{6}\)
= 120
The rate of production for #1 Toys is 120 toys per minute. The rate of production for Toys Plus is 123 toys per minute. Since 120 is less than 123, #1 Toys produces toys at a slower rate.
Question 4.
A train is traveling from City A to City B, a distance of 320 miles. The graph below shows the number of miles, y, the train travels as a function of the number of hours, x, that have passed on its journey. The train travels at a constant speed for the first four hours of its journey and then slows down to a constant speed of 48 miles per hour for the remainder of its journey.
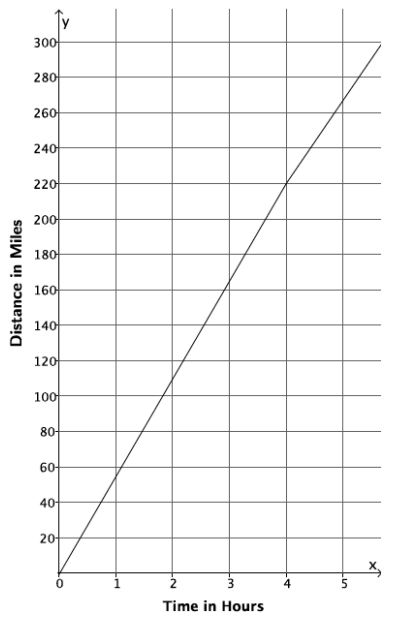
a. How long will it take the train to reach its destination?
Answer:
Student solutions will vary. Sample solution is provided.
We see from the graph that the train travels 220 miles during its first four hours of travel. It has 100 miles remaining to travel, which it shall do at a constant speed of 48 miles per hour. We see that it will take about 2 hours more to finish the trip:
100 = 48x
2.08333… = x
2.1 ≈ x.
This means it will take about 6.1 hours (4 + 2.1 = 6.1) for the train to reach its destination.
b. If the train had not slowed down after 4 hours, how long would it have taken to reach its destination?
Answer:
320 = 55x
5.8181818…. = x
5.8 ≈ x
The train would have reached its destination in about 5.8 hours had it not slowed down.
c. Suppose after 4 hours, the train increased its constant speed. How fast would the train have to travel to complete the destination in 1.5 hours?
Answer:
Let m represent the new constant speed of the train.
100 = m(1.5)
66.6666…. = x
66.7 ≈ x
The train would have to increase its speed to about 66.7 miles per hour to arrive at its destination 1.5 hours later.
Question 5.
a. A hose is used to fill up a 1,200 gallon water truck. Water flows from the hose at a constant rate. After 10 minutes, there are 65 gallons of water in the truck. After 15 minutes, there are 82 gallons of water in the truck. How long will it take to fill up the water truck? Was the tank initially empty?
Answer:
Student solutions will vary. Sample solution is provided.
Let x represent the time in minutes it takes to pump y gallons of water. Then, the rate can be found as follows:

\(\frac{65 – 82}{10 – 15}\) = \(\frac{ – 17}{ – 5}\)
= \(\frac{17}{5}\)
Since the water is pumping at a constant rate, we can assume the equation is linear. Therefore, the equation for the volume of water pumped from the hose is found by
65 = \(\frac{17}{5}\) (10) + b
65 = 34 + b
31 = b
The equation is y = \(\frac{17}{5}\) x + 31, and we see that the tank initially had 31 gallons of water in it. The time to fill the tank is given by
1200 = \(\frac{17}{5}\) x + 31
1169 = \(\frac{17}{5}\) x
343.8235… = x
343.8 ≈ x
It would take about 344 minutes or about 5.7 hours to fill up the truck.
b. The driver of the truck realizes that something is wrong with the hose he is using. After 30 minutes, he shuts off the hose and tries a different hose. The second hose flows at a constant rate of 18 gallons per minute. How long now does it take to fill up the truck?
Since the first hose has been pumping for 30 minutes, there are 133 gallons of water already in the truck. That means the new hose only has to fill up 1,067 gallons. Since the second hose fills up the truck at a constant rate of 18 gallons per minute, the equation for the second hose is y = 18x.
Answer:
1067 = 18x
59.27 = x
59.3 ≈ x
It will take the second hose about 59.3 minutes (or a little less than an hour) to finish the job.
Eureka Math Grade 8 Module 5 Lesson 7 Exit Ticket Answer Key
Question 1.
Brothers Paul and Pete walk 2 miles to school from home. Paul can walk to school in 24 minutes. Pete has slept in again and needs to run to school. Paul walks at a constant rate, and Pete runs at a constant rate. The graph of the function that represents Pete’s run is shown below.
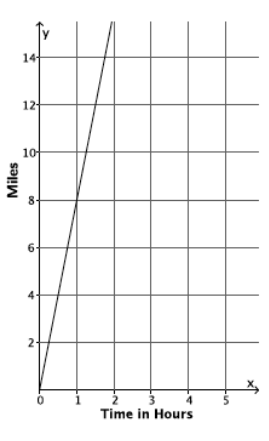
a. Which brother is moving at a greater rate? Explain how you know.
Answer:
Paul takes 24 minutes to walk 2 miles; therefore, his rate is \(\frac{1}{12}\) miles per minute.
Pete can run 8 miles in 60 minutes; therefore, his rate is \(\frac{8}{60}\), or \(\frac{2}{15}\) miles per minute.
Since \(\frac{2}{15}\)>\(\frac{1}{12}\), Pete is moving at a greater rate.
b. If Pete leaves 5 minutes after Paul, will he catch up to Paul before they get to school?
Answer:
Student solution methods will vary. Sample answer is shown.
Since Pete slept in, we need to account for that fact. So, Pete’s time would be decreased. The equation that would represent the number of miles Pete runs, y, in x minutes, would be
y = \(\frac{2}{15}\)(x – 5).
The equation that would represent the number of miles Paul walks, y, in x minutes, would be y = \(\frac{1}{12}\) x.
To find out when they meet, solve the system of equations:
y = \(\frac{2}{15}\) x – \(\frac{2}{3}\)
y = \(\frac{1}{12}\) x
\(\frac{2}{15}\) x – \(\frac{2}{3}\) = \(\frac{1}{12}\) x
\(\frac{2}{15}\) x – \(\frac{2}{3}\) – \(\frac{1}{12}\) x + \(\frac{2}{3}\) = \(\frac{1}{12}\) x – \(\frac{1}{12}\) x + \(\frac{2}{3}\)
\(\frac{1}{20}\) x = \(\frac{2}{3}\)
(\(\frac{20}{1}\)) \(\frac{1}{20}\) x = \(\frac{2}{3}\) (\(\frac{20}{1}\))
x = \(\frac{40}{3}\)
y = \(\frac{1}{12}\) (\(\frac{40}{3}\)) = \(\frac{10}{9}\) or y = \(\frac{2}{15}\) (\(\frac{40}{3}\)) – \(\frac{2}{3}\)
Pete would catch up to Paul in \(\frac{40}{3}\) minutes, which occurs \(\frac{10}{9}\) miles from their home. Yes, he will catch Paul before they get to school because it is less than the total distance, two miles, to school.
Eureka Math Grade 8 Module 5 Lesson 7 Multi – Step Equations II Answer Key
Question 1.
2(x + 5) = 3(x + 6)
Answer:
x = – 8
Question 2.
3(x + 5) = 4(x + 6)
Answer:
x = – 9
Question 3.
4(x + 5) = 5(x + 6)
Answer:
x = – 10
Question 4.
– (4x + 1) = 3(2x – 1)
Answer:
x = \(\frac{1}{5}\)
Question 5.
3(4x + 1) = – (2x – 1)
Answer:
x = – \(\frac{1}{7}\)
Question 6.
– 3(4x + 1) = 2x – 1
Answer:
x = – \(\frac{1}{7}\)
Question 7.
15x – 12 = 9x – 6
Answer:
x = 1
Question 8.
\(\frac{1}{3}\) (15x – 12) = 9x – 6
x = \(\frac{1}{2}\)
Question 9.
\(\frac{2}{3}\) (15x – 12) = 9x – 6
Answer:
x = 2