A triangle is a three-sided polygon that is having three sides, angles and vertices. An isosceles triangle is a triangle that has two sides of equal length and two angles of equal measure. Here we are providing the detailed proof for the statement If two isosceles triangles have the same base length, then the legs of one of the triangles are twice as long as the legs of the other.
If Two Isosceles Triangles on Same Base, Legs of One Triangle are Twice of Legs of Other
It is the proof for the statement Problem on Two Isosceles Triangles on the Same Base. The legs of one of the triangles are twice as long as the legs of the other.
Let us take two isosceles triangles △ABC and △BCD drawn on the same base BC and on the same side of it.
If A and D are joined, prove that each of the angles ∠BAC, ∠BDC will be divided by the line AD into two equal parts.
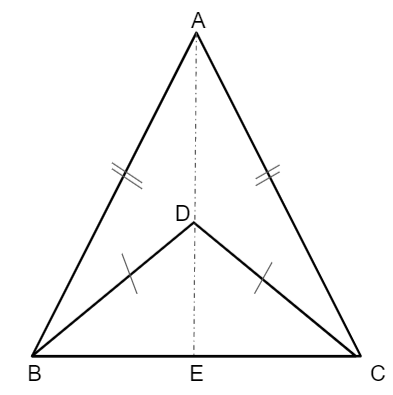
Given that,
AB = AC and BD = BC to prove ∠BAD = ∠CAD and ∠BDE = ∠CDE
| Statement | Reason |
|---|---|
| In ∆ABC, ∠ABC = ∠ACB = x° (Assume) | AB = AC |
| In ∆DBC, ∠DBC = ∠DCB = y° (Assume) | DB = CD |
| ∠ABC – ∠DBC = ∠ABC – ∠DCB = x° – y° | Subtracting statement 2 from statement 1 |
| Therefore, ∠ABD = ∠ACD = x° – y° | From statement 3 |
| In ∆ABD and ∆ACD AB = AC DB = DC ∠ABD = ∠ACD |
Given Given From statement 4 |
| ∆ABD ≅ ∆ACD | By SAS Criterion |
| ∠BAD = ∠CAD = z° (Suppose) | CPCTC |
| ∠BDE = ∠ABD + ∠BAD = x° – y° + z° | The exterior angle of a triangle is equal to the sum of the interior opposite angles. |
| Similarly, ∠CDE = ∠ACD + ∠CAD = x° – y° + z° | The exterior angle of a triangle is equal to the sum of the interior opposite angles. |
| ∠BDE = ∠CDE | From statements 8 and 9 |
Hence proved.
More Related Articles:
- Problems on Properties of Isosceles Triangles
- Equal Sides of an Isosceles Triangle
- Angles Opposite to Equal Sides of an Isosceles Triangle are Equal
Problems on Two Isosceles Triangles on the Same Base
Problem 1:
How to find the lengths of the sides of the isosceles triangles on the same base, if their perimeters are 23 cm, 41 cm.
Solution:
Given that,
Let the sides of the smaller isosceles triangle be a, b, b
The perimeter of the smaller triangle = 23 cm
Two Isosceles Triangles have the same base. The legs of one of the triangles are twice as long as the legs of the other.
The sides of bigger isosceles triangles are a, 2b, 2b
Perimeter of the bigger triangle = 41 cm
a + b + b = a + 2b = 23 — (i)
a + 2b + 2b = a + 4b = 41 — (ii)
Subtracting (ii) from (i)
a + 4b – a – 2b = 41 – 23
2b = 18
b = 9
Substitute b = 9 in (i)
a + 2 x 9 = 23
a + 18 = 23
a = 23 – 18 = 5
Therefore, the sides of the smaller triangle are (5, 9, 9) and the bigger triangle is (5, 18, 18).
Problem 2:
If two isosceles triangles are on the same base. The perimeter of a bigger isosceles triangle is 80 cm, base of the triangles is 15 cm. Find a smaller triangle perimeter, sides of both triangles?
Solution:
Given that,
The perimeter of the bigger isosceles triangle = 80 cm
The base of the triangle a = 15 cm
Let the smaller isosceles triangle sides be a, b, b
Two Isosceles Triangles have the same base. The legs of one of the triangles are twice as long as the legs of the other.
Then, bigger triangle sides are a, 2b, 2b
The perimeter of larger triangle = 80 cm
a + 2b + 2b = 80 cm
15 + 4b = 80
4b = 65
b = 16.25
The smaller triangle perimeter = a + b + b = a + 2b
= 15 + 2 x 16.25 = 47.5 cm
The sides of the bigger triangles are (15, 32.5, 32.5), smaller triangles are (15, 16.25, 16.25).